1.1.2. Анализ численных методов решения

При определении динамических характеристик конструкций МЭМС и НЭМС возникает необходимость в решении двух основных задач динамики: в первой находятся собственные частоты и собственные формы колебаний конструкции, во второй определяют амплитуды вынужденных колебаний элементов в различных точках конструкции при заданных параметрах внешнего вибрационного воздействия. Далее могут быть определены механические напряжения и запасы прочности конструктивных элементов, а также оценена вероятность безотказной работы устройства при вибрации.

При расчетах элементов конструкций МЭМС и НЭМС можно выделить два основных подхода: аналитический (расчет с помощью точных аналитических или приближенных эмпирических зависимостей) и моделирование на основе сеточной аппроксимации среды, когда исследуемый объект представляется сеточной аппроксимацией. При этом основными являются методы конечных (МКЭ), граничных (МГЭ), бесконечных (МБЭ) элементов и метод конечных разностей (МКР).

Практическое применение для решения задач динамики конструкций аналитических методов, к которым относятся методы разделения переменных, позволяют получить решение в виде формулы или группы формул, анализ которых дает наглядное представление о влиянии конструктивных параметров на характеристики динамических процессов и оптимизировать конструкции, сопряжено с рядом трудностей. Конструкции современной аппаратуры представляют собой сложные механические системы с множеством упругих и жёстких связей, с неклассическими для строительной механики способами крепления отдельных конструктивных элементов. Для такой механической системы сложно построить расчётную модель, достаточно простую и в то же время хорошо отражающую физические и динамические свойства, тем более, что конструкция содержит множество неконтролируемых параметров, например усилия затяжки соединений при сборке плат в пакет, коэффициенты механических потерь материалов элементов. При составлении и решении уравнений движения конструкции возникает ряд математических трудностей. Основной недостаток аналитических методов в трудности математического описания собственной формы колебаний и граничных условий для сложных конструкций. Поэтому аналитические методы наиболее часто применяют для конструкций простой формы с "классическими" способами крепления типа жесткого защемления, свободного опирания или незакрепленного края пластины или конца балки.

Численные методы, среди которых наибольшее применение получили методы конечных элементов (МКЭ), конечных разностей (МКР), граничных элементов, не имеют принципиальных препятствий для решения сложных конструкций со сложными способами крепления. Характерным для них является замена исходных дифференциальных уравнений алгебраическими за счет дискретизации конструкции. К недостаткам этих методов относятся [1-6]:

• необходимость решения большой системы алгебраических уравнений;

• решение получается в виде таблицы чисел, и любое изменение конструкции приводит к необходимости решения на ЭВМ;

• дискретизация приводит к погрешности, оценка которой часто более сложная задача, чем нахождение основного решения.

Поэтому применение численных методов целесообразно, если аналитические методы не пригодны. Это объясняет целесообразность параллельного развития как аналитических, так и численных методов. Можно ожидать наибольшего эффекта от разумного сочетания этих методов.

Эти причины способствовали быстрому развитию численных методов, которые и получили в настоящее время широкое распространение с внедрением в практику инженерных расчётов цифровых ЭВМ. Основу численных методов расчётов динамических параметров конструкции составляют: метод конечных разностей (МКР), метод конечных элементов (МКЭ) и различные вариационные методы, в том числе и энергетический метод.

Теория математических моделей физических явлений составляет предмет математической физики, которая развивалась со времён Ньютона параллельно развитию физики и математики. В конце XVII в. было открыто дифференциальное и интегральное исчисление. В XVIII в. методы математической физики начали формироваться при изучении колебаний струн и стержней; закладываются основы аналитической механики. В XIX в. идеи математической физики находят новое развитие в связи с задачами теплопроводности, диффузии, упругости, оптики, электродинамики; создаётся теория потенциала. В таблице 1.1 приведены основные этапы развития и методы решения полевых задач.

Таблица 1.1 Методы решения
Классические методы Аппроксимационная теория Специальные аналитические методы Преобразования	Михлин Binns Schwarz Christoffel	1967 1963 1869 1870
Графические методы	Johnson Bewley	1927 1948
Модели резистивных сеток	Liebman Duffin	1949, 1952 1959
Физические модели Электропроводящая бумага Электролитическая ванна	Karplus	1958
Метод конечных разностей	Binns Müller	1963 1983
Вариационные методы	Ritz McDonald	1909 1974
Статистические методы Метод Монте‑Карло	Ehrlich	1959

В развитии численных методов можно выделить следующие вехи:

С появлением ЭВМ появилась реальная возможность ставить вычислительные эксперименты. Многие методы уже перестали использоваться и служат только для обучающих целей, а для решения большинства практических задач используются методы, которые можно разделить на три основные группы: метод конечных разностей; метод конечных элементов; интегральные методы.

Для расчёта конструкций МЭМС и НЭМС с помощью метода конечных разностей строится его упрощенная модель-сетка. В этой модели детали с непрерывно распределенной массой заменяются набором дискретных элементов с сосредоточенными массами. Точки сосредоточения массы элементов называют узлами. Соседние узлы соединяются друг с другом невесомыми упругими связями. Таким образом, модель стержня будет представлять собой одномерную структуру в виде цепочки узлов (рис.5.3.5.1,а), модель платы или панели - плоскую сетку (рис.1.1.1,6), модель монолитного блока -пространственную трёхмерную сетку (рис.1.1.1,в).

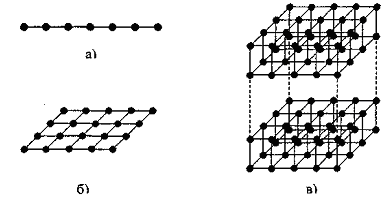
Рис.1.1.1. Сеточные модели элементов конструкций ЭС

(а) одномерные, б) двумерные, в)трехмерные).

Расчёт модели ведётся с помощью конечно-разностных уравнений. Эти уравнения образуют из дифференциальных уравнений посредством замены в них частных и обычных производных отношениями конечных приращений рассматриваемых переменных. Так, например, производная заменяется отношением конечных приращений и

Приращение аргумента - шаг берут обычно одинаковым во всём интервале изменения функции f(x):

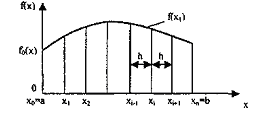
Рис.1.1.2. К определению конечных разностей в одномерной задаче

Приращение функции вычисляется с помощью одного из разностных операторов ,  или :

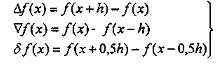
В соответствии с этим в любой точке x=x_t могут быть вычислены:

- разность, взятая вперед;

- разность, взятая назад; - центральная разность.

По этой же схеме вычисляются и разности высших порядков, например:

Используя эти выражения, можно получить формулы для приближенного вычисления производных в точке x=x_it.

Недостатком МКР является большая трудоемкость составления конечно-разностных уравнений при подготовке задачи к решению на ЭВМ. Наиболее известным программным комплексом, реализованным на использовании МКР, является "Асоника". При наличии сложного контура ступенчатого изменения жесткости решение задач динамики конструкции при помощи МКР встречает большие трудности. В этом случае рекомендуется применять метод конечных элементов.

Метод конечных разностей был самым первым методом численного решения полевых задач. В этом методе всю область решения разбивают на большое количество дискретных элементов. В трехмерном случае область решения разбивается на прямоугольные параллелепипеды. На получившейся таким образом трехмерной сетке, аппроксимируется дифференциальный оператор, как линейная комбинация значений функции в узловых точках. Этот метод можно применить к любой системе дифференциальных уравнений, однако, учет и подстановка краевых условий представляет собой достаточно сложную процедуру. Точность решения существенно зависит от параметров дискретизации области. При увеличении точности решения число уравнений увеличивается, растет размерность системы уравнений, при этом системная матрица остается сильно разряженной: для трехмерных задач только шесть элементов в каждой строке ненулевые, что позволяет использовать быстрые алгоритмы решения.

В качестве альтернативы методу конечных разностей можно отнести метод конечных элементов. В этом методе, как и в методе конечных разностей, вся область решения делится на большое количество дискретных элементов (конечных элементов). Обычно используют простейшие элементы такие, как треугольники или четырехугольники для двумерных задач и элементы типа тетраэдров или гексаэдров для трехмерных задач. На получившейся таким образом сетке определяется множество базисных функций. Решение задачи будет линейной комбинацией этих функций. Определение соответствующих коэффициентов осуществляют либо минимизацией энергетического функционала, либо методом взвешенных невязок с произвольной весовой функцией. Метод конечных элементов по праву считается самым универсальным методом для решения полевых задач. Точность решения, как и для метода конечных разностей, зависит от параметров дискретизации области решения. Как и в методе конечных разностей, системная матрица сильно разрежена и представляет собой полосовую матрицу. Ширина полосы зависит от разности номеров узловых точек в одном элементе. Кроме того, системная матрица симметрична относительно главной диагонали. Учитывая все особенности системной матрицы, так же можно использовать быстрые алгоритмы решения.

Рис.1.1.3.

В противоположность вышеописанным методам можно отнести методы третьей группы, т.е. интегральные методы решения. Безусловно, метод конечных разностей уже устарел и используется лишь в качестве учебного средства, чего нельзя сказать о методе конечных элементов. За последнее время метод конечных элементов совершенствовался и приобрел большой успех у исследователей. С помощью метода конечных элементов решено и решается большое количество практических задач. При этом большинство исследователей полагают, что нет альтернативы методу конечных элементов. Однако эти утверждения верны лишь частично. Ряд практических задач с достаточной эффективностью можно решить и интегральными методами. В то время как основные свойства дифференциальных уравнений были известны уже с XVII в., лишь в 1905 году Фредгольм описал первые исследования свойств интегральных уравнений. В 1963 году Jaswon в своей работе, посвященной сингулярным интегральным уравнениям в потенциальной теории, предложил использовать интегральные методы, как численные методы решения задач математической физики, что и положило основу к их активному изучению и применению. В этой работе метод решения был назван “Boundary Integral Equation Method” или в краткой форме BIEM, что означает Метод Граничных Интегральных Уравнений.

В методе конечных элементов исходная область определения функции разбивается сеткой, в общем случае, в отличие от МКР неравномерной, на отдельные участки - конечные элементы. Искомая непрерывная функция заменяется кусочно-непрерывной, определенной для множества конечных элементов. Чаще всего для этого используются полиномы, обеспечивающие непрерывность искомой формы колебаний в узлах на границах элементов. Для одномерных функций конечными элементами являются отрезки прямой, для двумерных областей наиболее часто конечные элементы представляются в виде треугольников и четырехугольников, для трехмерных — в виде тетраэдра или параллелепипеда.

Алгоритм МКЭ включает пять этапов.

1. Разбиение заданной области на макроэлементы (области с близкими свойствами и геометрией)

2. Разбиение заданной области, например, площади ячейки, на конечные элементы.

3. Выбор аппроксимирующей функции в виде полинома для каждого элемента.

4. Объединение полученных полиномиальных функций в систему алгебраических уравнений.

5. Решение полученной системы уравнений и определение вектора узловых значений функции (перемещений, ускорений).

Отметим, что наиболее сложным этапом является четвертый, требующий глубоких знаний в области механики сплошной среды.