Моделирование физико-механических компонентов наносистем

Цель дисциплины - изучение математических моделей физико-механических компонентов наносистем, методов и алгоритмов, лежащих в основе моделирования наносистем.

Предметом изучения являются математические модели, используемые для инженерного анализа наносистем.

Задачи дисциплины – формирование знаний, умений и навыков по следующим направлениям деятельности:·

1. теоретическая подготовка по фундаментальным положениям теории построения моделей микро- и наносистем;·

2. методы моделирования физико-механических компонентов микро- и наносистем;

3. изучение различных моделей физико-механических компонентов микро- и наносистем;·

4. изучение различных алгоритмов расчета процессов в микро- и наносистемах;·

5. получение навыков выбора корректных моделей для физико-механических компонентов микро- и наносистем.

1. Введение в теорию моделирования физико-механических компонентов микро- и наносистем

Модель (ММ) – это условный образ исследуемого технического объекта (ИТО), конструируемый исследователем так, чтобы отобразить его характеристики (свойства, взаимосвязи, параметры), существенные для исследователя.

Модель может быть физическим объектом (ФО) (макет, стенд) или спецификацией – функциональная, поведенческая, структурная и др.

Моделирование – метод исследования процессов или явлений в ИТО на моделях (физических или математических).

Математические модели могут быт геометрическими, топологическими, динамическими, логическими и др.

Информационные модели – таблицы и диаграммы вида «сущность-отношение»

Функциональная математическая модель – это алгоритм вычисления вектора выходных параметров Y при заданных векторах параметров элементов X и внешних параметров Q.

Физическая модель – устройство или приспособление, воспроизводящее в том или ином масштабе ИТО при сохранении физического подобия процессов в ФО процессам в ИТО.

Для оценки адекватности результатов исследования на ФМ реальному процессу вводится критерий подобия, содержащий комбинацию значений физических параметров, характеризующих ИТО.

Например, течение вязкой жидкости в двух трубах диаметром d1 и d2 будут подобны, если совпадут значения чисел Рейнольдса для обеи труб (отношение (V1d1/1) = (V2d2/2), где  – кинематическая вязкость; V - скорость потока жидкости.

Физическое моделирование – исследование процессов и явлений в ИТО с помощью ФМ при равенстве критерия подобия ФМ и ИТО.

Изоморфность ММ – одинаковое по форме математическое описание для разных по природе физических явлений.

Переменные в ММ – координаты пространства поведения ММ – это величины, подлежащие изменению или определению при решении задач ИТО.

Выходные переменные – величины, характеризующие состояние ИТО и подлежащие определению в процессе моделирования ИТО.

Входные переменные – величины, целенаправленно изменяемые самим исследователем (в соответствии с алгоритмом моделирования) при решении задач ИТО с помощью ММ.

Параметры ММ – постоянные величины (или заранее заданные функции времени), обычно не изменяемые в процессе исследования системы (бывают внешние (Q), внутренние (X) и выходные (Y)).

Априорная модель – модель, построенная (выбранная) до начала исследований.

Аддитивность величин – свойство, заключающееся в том, что значение выходной переменной целого ИТО равно  соответствующих выходных величин составных его частей.

Полная идентификация ММ – определение параметров и структуры ММ ИТО, обеспечивающих наилучшее совпадение выходных координат ИТО и ММ при одинаковых входных воздействиях.

Параметрическая идентификация ММ – определение параметров ММ при заданной ее структуре, обеспечивающих наилучшее совпадение выходных координат ИТО и ММ при одинаковых входных воздействиях.

Апостериорная модель – модель, улучшенная по результатам экспериментальных исследований (уточненная).

«Черный ящик» – это ИТО, у которого при неизвестных внутренней организации, структуре и характере поведения элементов имеется возможность наблюдать или контролировать реакцию выходных элементов на изменение входных воздействий.

Перечислим требования к ММ указанных классов:

- полнота модели – ММ должна обеспечивать возможность получения необходимого и достаточного набора оценок характеристик ИТО с требуемой точностью при заданной достоверности;

- гибкость модели – ММ должна давать возможность воспроизведения различных ситуаций при изменении структуры (алгоритмов) ММ и параметров ИТО;

- точность модели – ММ должна допускать возможность замены, добавления и исключения частей ММ без смены всей модели

. наконец, ММ должна обеспечивать эффективность машинного эксперимента.

ММ-е конструкции ИТП микро- и наносистем целесообразно использовать:

- для исследования ТО до того как он спроектирован с целью обеспечения чувствительности выходных характеристик ТО к изменению параметров ИТО и внешней среды;

- на этапе проектирования ТО для анализа и синтеза альтернативных вариантов построения ТО и выбора среди них одного, удовлетворяющего выбранному критерию эффективности;

- для прогнозирования развития ИТО во времени.

Переменные математических моделей (координаты пространства поведения математических моделей) – это величины, подлежащие изменению или определению при решении задач исследуемых физических объектов.

Выходные переменные – это величины, характеризующие исследуемый технический объект и подлежащие определению в процессе моделирования исследуемого физического объекта.

Входные переменные – это величины, целенаправленно изменяемые (самим исследователем, в соответствии с моделируемым алгоритмом) при решении на математической модели задач исследуемого технического объекта.

Параметры математической модели – постоянные величины (или заранее заданные функции, временные изменения которых дополняются между решениями задач моделирования).

Априорная модель – модель, построенная до начала специального экспериментального исследования или выбранная априорно исследователем.

Аддитивность величин – свойство, заключающееся в том, что значения направленной выходной переменной величины целого исследуемого технического объекта равно сумме соответственных выходных величин, - частей целого объекта равно n- значениям величин соответствующих частей целого при разбиении объекта на части.

Идентификация математической модели (полная) - означает определение параметров и структуры математической модели исследуемого технического объекта, обеспечивающих наилучшее совпадение выходных координат исследуемого технического объекта и математической модели при одинаковых входных воздействиях.

Параметрическая идентификация математической модели – определение параметров математической модели при заданной ее структуре, обеспечивающих наилучшее совпадение выходных координат исследуемого технического объекта и математической модели при одинаковых входных воздействиях.

Апостериорная модель – (математическая модель) – модель, улучшенная по результатам экспериментов (уточненная).

Аппроксимированная (гипотетическая) математическая модель - упрощенная, приближенная математическая модель.

«Черный ящик» – это исследуемый технический объект, у которого при неизвестной внутренней организации, неизвестной структуре и неизвестном характере поведения элементов имеется возможность наблюдать или контролировать реакцию выходных элементов на изменение входных.

Место математического моделирования в инженерном анализе – определение места инженерного анализа (ИА) в процессе создания и жизни ЭВА.

З амысел

Р азработка (проектирование) <=> инженерный анализ

И зготовление (производство)

Э ксплуатация

С нятие с эксплуатации

Определим графически место моделирования в инженерном анализе:

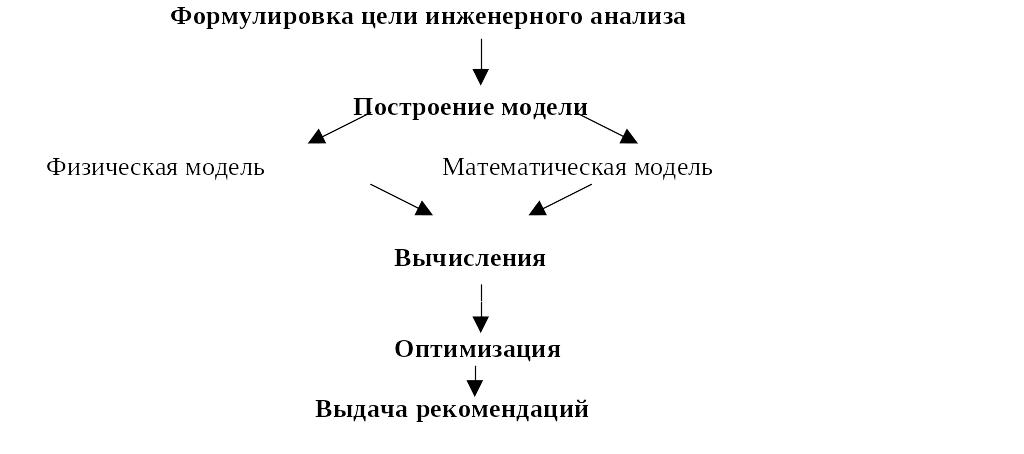
Рис.1.1. Место моделирования в инженерном анализе.

Последовательность разработки и машинной реализации математической модели исследуемого объекта интересующего нас класса. Нас интересуют следующие классы исследуемых технических объектов:

1. Конструирование ЭВА.

2. Технологические процессы изготовления ЭВА.

Основные требования, предъявляемые к математическим моделям исследуемых технических объектов интересующего нас класса:

1. Полнота математической модели должна представлять возможность получения необходимого набора оценок характеристик исследуемого технического объекта с требуемой точностью и достоверностью.

2. Гибкость математической модели должна давать возможность воспроизводства различных ситуаций при варьировании структуры (алгоритма) математической модели, параметров исследуемого технического объекта.

3. Структура математической модели должна быть блочной, т.е. допускать возможность замены, добавления и исключения некоторых частей без перемены всей модели

4. Определенные требования к программному обеспечению с целью увеличения обеспечения эффективности машинного эксперимента.

Математическое моделирования конструкции исследуемого технического производства ЭВА целесообразно использовать в следующих случаях:

А) - для исследования технического объекта до того, как он спроектирован с целью обеспечения чувствительности выходных характеристик к изменению параметров исследуемого технического объекта и внешней среды.

Б) – на этапе проектирования для анализа и синтеза альтернативных вариантов построения и выбора среди них одного, который удовлетворяет заданному критерию оценки эффективности функционирования исследуемого технического объекта.

В) – для прогноза развития исследуемого технического объекта во времени.

Как правило, результаты разработки конструкции РЭА получаются неоднозначными и приходится принимать решение об их пригодности на основе испытаний опытных образцов. Однако ввиду высокой сложности этих конструкций, реализующих зачастую целые системы, изготовление опытных образцов весьма трудоемко и дорогостояще. Поэтому, целесообразно до изготовления изделия проводить анализ проектируемых конструкций на основе аналогового или цифрового моделирования на ЭВМ протекающих в ней физических процессов под воздействием внешних и внутреннмх дестабилизирующих факторов. Результаты такого моделирования призваны заменить на стадии проектирования дорогостоящие испытания. (Прототипирование).

Выявляя сильные и слабые стороны получаемых в результате моделирования вариантов конструкции, можно принять более обоснованное решение.

Любое устройство ЭВА работает в условиях влияния внутренних и внешних факторов, имеющих различную физическую природу.

К внешним факторам относятся параметры окружающей среды (температура и влажность), механические воздействия (вибрация, удары, деформирующие силы …), внешние электромагнитные поля.

Внутренние факторы связаны с источниками энергии внутри рассматриваемой конструкции, к которым относятся тепловыделяющие элементы конструкции, источники внутренних электростатических, магнитных и электромагнитных полей.

Под воздействием перечисленных факторов изменяется надежность устройства и его характеристики. То есть, степень пригодности выбранной конструкции определяется ее реакцией на внутренние и внешние возмущения.

Процесс работы устройства ЭВА в реальных условиях можно представить следующей схемой:

Внутренние и внешние возмущения		Система параметров устройства ЭВА		Реакция конструкции
 

В процессе анализа конструкции ЭВА нас будет интересовать правая часть данной схемы – то есть выявление реакции конструкции на заданные возмущения. С этой целью проведем классификацию процессов, протекающих в ЭВА. Эти процессы подразделяются на стационарные и нестационарные. Процесс называется стационарным, если внешние и внутренние возмущения практически не изменяются во времени, то есть наблюдается состояние установившегося режима работы конструкции. Если внешние или внутренние возмущения изменяются во времени, стационарность условий работы ЭВА нарушается – такие условия или процессы называются нестационарными.

Для моделирования задач анализа конструкций ЭВА отличие между стационарными и нестационарными условиями является существенным, поскольку методы их решения различны.

В первом случае, когда реакция системы, а также внешние и внутренние возмущения не меняются во времени, задачу определения реакции системы называют краевой задачей. Для решения таких задач достаточно найти величину реакции и ее распределение в конструкции. Примером краевой задачи может служить задача определения распределения температур в блоке ЭВА при заданном установившемся режиме работы и постоянной температуре окружающей среды. Краевыми условиями здесь являются температура окружающей среды или плотность потока тепловой энергии обмена с окружающей средой.

Во втором случае, когда реакция системы является функцией времени, задачу определения реакции системы называют задачей с начальными условиями (НУ). В таких задачах для определения реакции системы необходимо знать ее поведение в начальный и последующие интервалы времени.

Напрмер, когда температура источников тепла в блоке и окружающей среде меняются во времени, задача носит нестационарный характер и является задачей с начальными условиями (условия Коши). В такой задаче требуется определить температуру в блоке в каждый момент времени при заданной температуре в начальный момент времени.

Задача анализа процессов в конструкциях ЭВА чаще всего сводится к исследованию различных полей (тепловых и электромагнитных) или механических явлений (вибрации и распределение напряжений в конструкции). Указанные процессы описываются с помощью диффернциальных уравнений (ДУ), поэтому их анализ сводится к решению ДУ в частных производных. Подобные уравнения в отличие от обыкновенных дифференциальных уравнений содержат не одну переменную, и результатом их решения является определение функции от нескольких переменных. В состав таких уравнений входят частные производные по каждой переменной.

Многие нестационарные физические процессы в пространстве описываются с помощью ДУ вида:

d / dX [ A₁(x,y,z,f,t) d / dX] + d / dY [ A₂(x,y,z,f,t )d / dY]+

+ d/dZ [A₃(x,y,z,f,t)d/dZ] = a (d² / dt²) +b (d / dt ) + c  + d (1)

где:

a= ₁(x,y,z,f,t)  0 b= ₂(x,y,z,f,t)  0

c= ₃(x,y,z,f,t)  0 d= ₄(x,y,z,f,t)  0

Функции A₁, A₂, A₃ определяют параметры вещества пространства. Если среда изотропная, то A₁= A₂=A₃ = const >0. В противном случае A₁ A₂A₃, причем полагают A₁ = const >0, A₂ = const >0, A₃ = const >0. В первом случае говорят о плоской (линейной) задаче.

Значение искомой функции  находится внутри некоторой области V, ограниченной поверхностью S – для трехмерной, и линией S – для двумерной задачи. На границе поверхности (линии) S задаются граничные условия вида:

( +   d/dn)_S = Ф, где:  и  - заданные функции точки в граничной области; Ф=Ф(x,y,z,f,t) – некоторая функция, значение которой в граничной области известны; d/dn – производная искомой функции по нормали к граничной области в рассматриваемой точке.

Если во всех точках граничной поверхности = 0, то есть функция Ф во всех точках определяет значение искомой функции , то такие условия называются граничными условиями первого рода: _S = Ф_1. Если же во всех точках граничной поверхности _S = 0, то есть определены лишь значения производной искомой функции по нормали к этой области, то такие условия считают граничными условиями второго рода: d/dn_S = Ф₂. В том случае, когда имеют место смешанные варианты условий, заданные выражением граничных условий общего вида, то их называют граничными условиями третьего рода.