2.4. Постановка задач расчета теплового процесса на дискретной модели

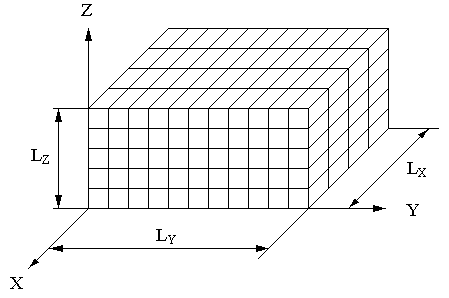
В электронно-вычислительной аппаратуре могут происходить следующие процессы передачи тепла: конвекция, кондукция и лучеиспускание. Разностный метод не применим для расчета передачи тепла конвекцией и лучеиспусканием. Поэтому ограничимся рассмотрением конструкций, элементы которых помещены либо в твердый наполнитель, например, в пенопласт, компаунд или резину, либо в желеобразный наполнитель с малым коэффициентом текучести. То есть будем рассматривать конструкции, в которых происходит только передача тепла теплопроводностью (кондукция). Предположим, что блок ЭВА имеет прямоугольную форму, внутри которого находятся источники тепла – радиоэлементы, через которые протекает электрический ток. Блок залит наполнителем с коэффициентом теплопроводности К и удельной теплоемкостью С. Разобьем мысленно конструкцию на части прямоугольной формы, каждую из которых назовем элементом.

	.
Рис.2.4.1.	Рис.2.4.2.

Для более высокой точности расчета выберем элементы одинаковых размеров, причем сами размеры элементов примем минимально возможными. В центре элемента выделим особую точку – узел сетки. Далее, попытаемся определить температуру в каждом узле сетки в каждый момент времени. Для простоты будем считать, что блок однороден, то есть входящие в него материалы имеют одинаковую теплоемкость и коэффициент теплопроводности. Температуру, определяемую в узле сетки с координатами x, y, z, в момент времени t, обозначим как ^t_X,Y,Z, а в следующий момент времени как ^t+1_X,Y,Z. Размеры блока, координаты и мощность тепловыделяющих радиоэлементов будем считать заданными. Кроме того, для решения задачи должны быть заданы начальные и граничные условия.

В начальных условиях задачи необходимо указать температуру во всех узлах сетки блока в начальный момент времени. Обычно при рассмотрении переходных процессов за начальный момент времени выбирается момент включения электрических цепей под нагрузку. До этого момента температура во всех узлах считается одинаковой и равной наружной температуре, например, комнатной (20^ОС или 293^ОК).

В граничных узлах блока могут быть заданы различные граничные условия. Когда на границе задается значение самой функции, то есть температура – это граничное условие 1-го рода и решение получается наиболее простым. Однако, к сожалению, только при грубом упрощении нестационарной задачи (то есть задачи с изменением температуры во времени) можно считать температуру на поверхности бока заданной, например, равной наружной температуре. Наиболее близкими к реальным условиям являются граничные условия 2-го рода, когда задаются плотности теплового потока по всей наружной поверхности блока. Далее мы будем решать задачу с граничными условиями 2-го рода.

2.4.1 Уравнение теплопередачи тепла через элемент дискретной модели

Запишем типовые уравнения движения теплоты. Для этого воспользуемся законом сохранения энергии: количество притекающей к данному элементу тепловой энергии равно количеству утекающей энергии плюс количество накапливающейся энергии. В рассматриваемом случае тепловая энергия не превращается в другие виды энергии, однако, другие виды энергии могут превращаться в тепло. Например, электрическая энергия целиком превращается в тепло, поэтому в уравнении теплового баланса нужно учесть количество энергии, выделяемой за счет электрических потерь.

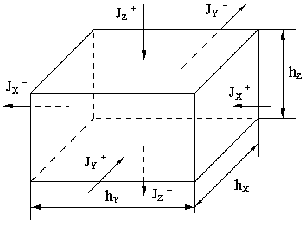
Рассмотрим прямоугольный элемент объема блока (рисунок 2.4.1). Количество энергии, притекающей и утекающей через боковые поверхности этого элемента, выражается через величину плотности тепловых потоков. Удельная плотность теплового потока J [Дж/м²сек ] определяется количеством теплоты, проходящей через единичную площадь в единицу времени. Чтобы определить количество теплоты, проходящей через боковую грань элемента за некоторое время, необходимо соответствующую плотность теплового потока умножить на площадь грани и на интервал времени:

(J_X⁺ – J_X^–) h_Yh_Z + (J_Y⁺ – J_Y^–) h_Xh_Z + (J_Z⁺ – J_Z^–) h_Xh_Y = C  (1)

где: J – удельная плотность тепловых потоков,  - время,  - приращение температуры.

В правой части уравнения (1) записано количество теплоты, накапливаемой внутри элемента за время .

Выполним в уравнении (1) следующие преобразования:

1. Приведем количество теплоты в левой и правой части уравнения к единичному объему и к единице времени, для этого разделим все члены. Для этого разделим все члены на объем элемента h_Xh_Zh_Y и на интервал времени .

2. Представим приращение температуры  в узле с координатами i, j, k за интервал времени  в виде разности температур в начале и в конце этого интервала:

 =  ^t+1 _{i, j, k} –  ^t _{i, j, k}

В результате получим уравнение:

(JX+ – JX–)	+	(JY+ – JY–)	+	(JZ+ – JZ–)	= CУД	ijkt+1–ijkt	(2)
hX		hY		hZ		

Теперь в правой части уравнения (15) стоит не теплоемкость элемента, а удельная теплоемкость вещества (наполнителя), составляющего элемент. В целом правая часть определяет количество теплоты, которое накапливается в единичном объеме в единицу времени в том месте теплового поля, где расположен рассматриваемый элемент. Теперь можно учесть то тепло G, которое выделяется в радиоэлементах за счет превращения электрической энергии в тепловую. Поскольку удельное тепловыделение определяется через количество теплоты, выделяемой в единичном объеме за единицу времени, то можно прибавить соответствующий член к левой части уравнения (15). Приходим к выражению:

(JX+ – JX–)	+	(JY+ – JY–)	+	(JZ+ – JZ–)	+G = CУД	ijkt+1–ijkt	(3)
hX		hY		hZ		

Удельное тепловыделение G стоит в левой части уравнения потому, что оно вносит теплоту в рассматриваемый объем.