4. Полигон и гистограмма.

Полигоном частот (относительных частот) называется ломаная линия с вершинами в точках ( , ), где – варианта, – ее частота, или ( , ), где - относительная частота.

Пример 1. Построить полигон частот для статистического распределения дневных температур в июне месяце:

 

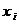
	20º	23º	24º	26º	27º	30º
	1	4	5	8	10	2

 

 

20 23 24 26 27 30

 

Для непрерывных распределений более наглядное представление о характере распределения случайной величины дает гистограмма.

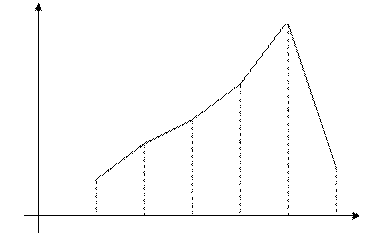
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников с основаниями длиной и высотой , где - длина каждого частичного интервала.

Пример 2. Построить гистограмму частот для статистического распределения из примера 1.

Решение: .

 

интер-вал	200-220	220-240	240-260	260-280	280-300
	1	6	7	14	2
	1/2	3	7/2	7	1

 

 

 

 

 

 

 

 

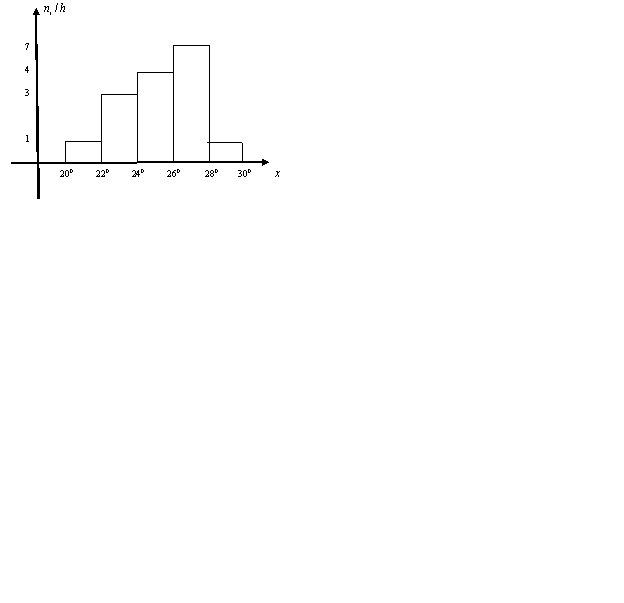
Если соединить середины верхних прямоугольников гистограммы, то получим полигон частот.

 

 

 

 

5. Средние величины вариационного ряда

 

Основной характеристикой вариационного ряда является его средняя арифметическая, называемая также выборочной средней.

Для дискретного выборочного ряда средняя арифметическая равна ,

а для интервального ряда

В последней формуле за принимают середину –го интервала.

Вариационным размахом называется число

Выборочной дисперсией называется средняя арифметическая квадратов отклонений вариант от их выборочной средней:

где – это значение варианта для дискретного ряда или середина i-го интервала для интервального ряда.

Для практических вычислений более удобной является следующая формула:

Свойства:

1. Дисперсия постоянной равна нулю.

2. Если ко всем вариантам добавить постоянное число, то дисперсия не изменится.

3. Если все варианты умножить на одно и то же число , то дисперсия умножится на .

4. (Правило сложения дисперсий).

Пусть значения выборки разбиты на групп. Обозначим через количество различных вариант в й группе, через - частоту -й варианты в этой группе. Тогда я группа ряда записывается в виде , при этом значение повторяется раз. Обозначим через групповые средние арифметические: .

Групповые дисперсии равны .

Средняя арифметическая групповых дисперсий равна

.

Межгрупповая дисперсия равна .

Правилом сложения дисперсий называется равенство

Оно служит основой для дисперсионного анализа.

Мерой вариации признака является выборочное среднее квадратическое отклонение, которое определяется как корень из дисперсии:

В статистическом анализе рассматривается также коэффициент вариации, равный процентному отношению выборочного среднего квадратического отклонения к выборочной средней:

 

Пример 3: В таблице приведены данные об урожайности ржи на различных участках поля.

 

 

 

Урожайность ржи, ц/га	[9-12]	[12-15]	[15-18]	[18-21]	[21-24 ]	[24-27]
Доля участка в общей пло-щади, %	6	12	33	22	19	8

 

Найти выборочную дисперсию, коэффициент вариации и размах вариации признака , обозначающего «урожайность ржи».

Выборочное среднее по формуле равно

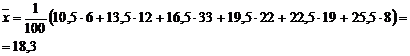
По формуле

вычислим выборочную дисперсию:

Тогда и коэффициент вариации равен

Размах вариации