Тема 9: «законы распределения непрерывных случайных величин» «законы распределения непрерывных случайных величин»

 

1. Показательный закон распределения.

2. Нормальный закон распределения.

3. Нормальная кривая.

4. Правило трех сигм.

 

1. Показательный закон распределения.

Непрерывная случайная величина имеет показательный закон распределения с параметром , если ее плотность вероятности имеет вид:

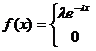
Функция распределения случайной величины , имеющей показательный закон распределения, равна:

ее математическое ожидание , дисперсия:

 

 

 

2. Нормальный закон распределения.

Нормальным называют распределение вероятностей непрерывной случайной величины , которое описывается плотностью 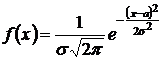, где - математическое ожидание; - среднее квадратическое отклонение случайной величины .

 

 

 

3. Нормальная кривая.

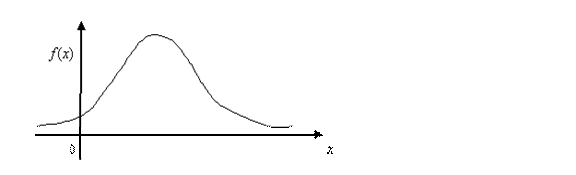
Кривая имеет вид, изображенный на рисунке. Эта кривая называется кривой Гаусса

Вероятность того, что примет значения, принадлежащее интервалу :

где функция Лапласа.

Значения функции Лапласа находятся по таблицам.

Вероятность того, что абсолютная величина отклонения меньше положительного числа , может быть вычислена по формуле .

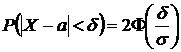В частности, при а=0 справедливо равенство

Задача 1. Случайная величина распределена по нормальному закону с математическим ожиданием и дисперсией . Вычислить вероятность попадания случайной величины в интервал (30; 80).

Решение:

Здесь

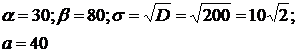
Применим формулу

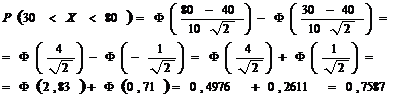
Медианой М_е(Х) называют то возможное значение , при котором ордината делит пополам площадь, ограниченную кривой распределения. Так как нормальная кривая (график функции ) симметрична относительно прямой , то ордината делит пополам площадь, ограниченную нормальной кривой, значит, .

Модой называют то возможное значение , при котором дифференциальная функция имеет максимум.

Мода и медиана для нормального распределения совпадают с математическим ожиданием.

 

 

4. Правило «трех сигм».

Если случайная величина имеет нормальный закон распределения с параметрами и , т.е. , то практически достоверно, что ее значения заключены в интервале :

 

 

Тема 10: «закон больших чисел» «закон больших чисел»

 

1.     Неравенство Чебышева.

2.     Теорема Чебышева и ее сущность.

3.     Значение теоремы Чебышева для практики.

4.     Теорема Бернулли.

Под законом больших чисел (ЗБЧ) понимается совокупность предложений, в которых утверждается, что с вероятностью, сколь угодно близкой к 1, отклонение средней арифметической достаточно большого числа случайных величин от постоянной - средней арифметической их математических ожиданий- не превышает как угодно малого числа >1.

 

 

1. Неравенство Чебышева.

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.

Рассмотрим дискретную случайную величину , заданную таблицей распределения:

Поставим перед собой задачу оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа . Если достаточно мало, то мы оценим, таким образом, вероятность того, что примет значения, достаточно близкие к своему математическому ожиданию. П.Л.Чебышев доказал неравенство, позволяющее дать интересующую нас оценку.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа , не меньше, чем :