2. Теорема Чебышева и его сущность
Теорема Чебышева. Если Х1, Х2, …, Хn - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число , вероятность неравенства
будет
как угодно близка к единице, если число
случайных величин достаточно велико.
Другими словами, в условиях теоремы
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.
Сущность
теоремы Чебышева
такова: хотя отдельные независимые
случайные величины могут принимать
значения, далекие от своих математических
ожиданий, среднее арифметическое
достаточно большого числа случайных
величин с большой вероятностью принимает
значения, близкие к определенному
постоянному числу, а именно к числу
(или
к числу
в частном случае). Иными словами, отдельные
случайные величины могут иметь
значительный разброс, а их среднее
арифметического рассеянно мало.
Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое.
Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.
Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин; она является ярким примером, подтверждающим справедливость учения диалектического материализма о связи между случайностью и необходимостью.
3. Значение теоремы Чебышева для практики.
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.
В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
4. Теорема Бернулли.
Пусть
производится
независимых испытаний, в каждом из
которых вероятность появления события
равна
.
Можно ли предвидеть, какова примерно
будет относительная частота появления
события?
Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846г.
Теорема Бернулли. Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Другими словами, если - сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство
Задача 1. Длина изготовляемых изделий представляет случайную величину, среднее значение которой (математическое ожидание) равно 90 см. Дисперсия этой величины равна 0,0225. Оценить вероятность того, что длина изделия выразится числом, заключенным между 89,7 см. и 90,3 см.
Решение:
Случайная величина
- длина изготовляемых изделий,
,
.
По условию задачи случайная величина
заключена между числами 89,7 и 90,3, т.е.
.
Вычитая 90 из неравенства, получим:
или
.
Заменим
это неравенство равносильным
и применим к нему неравенство Чебышева,
т.е.:
,
т.е.
Задача 3. Вероятность вызревания кукурузного стебля с тремя початками равна ¾. Оценить вероятность того, что среди 3000 стеблей, доля стеблей с тремя початками будет по абсолютной величине отличаться от вероятности вызревания такого стебля не более, чем на 0,02.
Решение:
- доля стеблей с тремя початками, т.е.
относительная частота.
;
;
,
.
Воспользуемся неравенством из теоремы Бернулли:
,
.
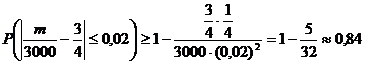Вероятность отклонения не менее 0,84, т.е. найдена нижняя граница вероятности.