2. Теорема Поста о полноте

Перейдем к рассмотрению одного из основных вопросов алгебры логики – вопроса о необходимых и достаточных условиях полноты. Пусть

– произвольная система функций из . Спрашивается, как выяснить, будет она полной или нет? Ответ на этот вопрос дает следующая теорема.

Теорема Поста. Для того чтобы система функций была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов .

Доказательство. Необходимость. Пусть – полна, то есть . Допустим, что содержится в одном из указанных классов – обозначим его через , то есть . Тогда в силу свойств замыкания и замкнутости имеем

.

Отсюда , что не так. Необходимость доказана.

Достаточность. Пусть целиком не содержится ни в одном из указанных классов. Тогда из можно выделить подсистему , содержащую не более пяти функций, которая обладает этим свойством. Для этого возьмем в функции , , , , и положим

.

Для доказательства достаточности убедимся, что из функций можно построить отрицание и конъюнкцию. Доказательство проведем в два этапа.

1. Построение при помощи функций , , и констант и отрицания.

Рассмотрим функции и . Построим функции одного аргумента:

и .

При сделанных предположениях

, .

В зависимости от того, какие значения имеют и , возможны четыре варианта.

1. , .

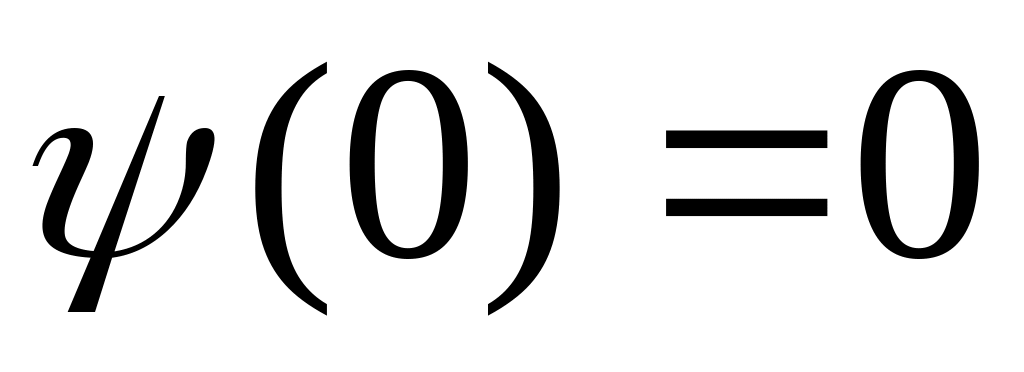В этом случае , . В результате суперпозиции получаем константу 1: . Таким образом, отрицание и константы построены.

2. , .

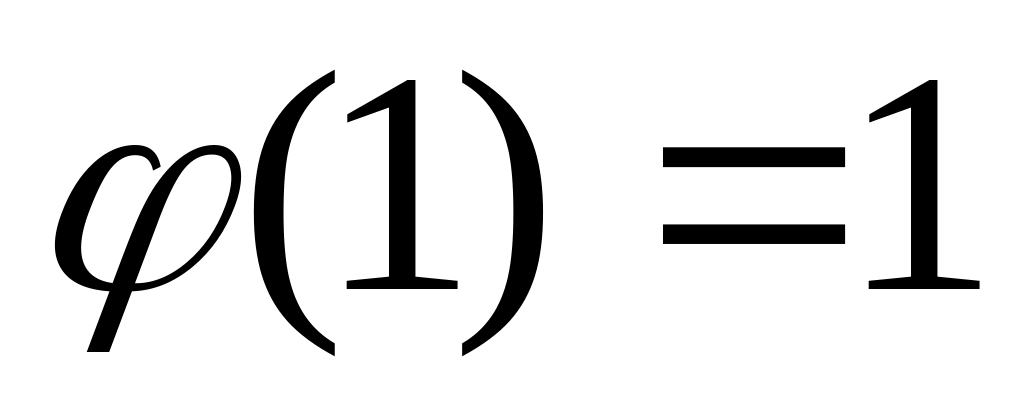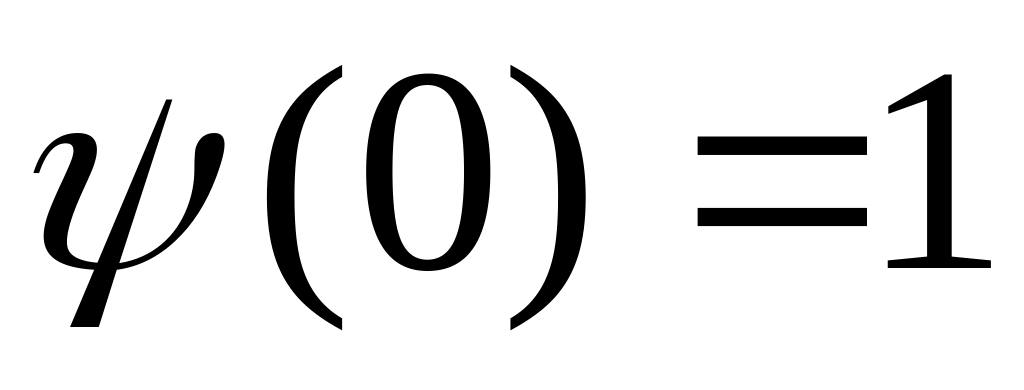В этом случае , . Строим , и первый этап закончен.

3. , .

Имеем . Воспользуемся функцией . Для этой функции найдется пара противоположных наборов и , на которых принимает одно и то же значение, так как

.

Рассмотрим функцию , в которой на место -го аргумента ставится , если , или , если . Тогда

.

Отсюда следует, что . С помощью отрицания построим другую константу.

4. , .

Следовательно, , . Воспользуемся немонотонной функцией . По лемме 4 из путем подстановки констант можно получить отрицание.

2. Покажем, что из функций можно построить конъюнкцию. При этом будем использовать построенные на первом этапе константы и отрицание. Воспользуемся нелинейной функцией . Подставим в нее константы и построим нелинейную функцию от двух аргументов, что возможно по лемме 6:

.

Рассмотрим функцию . Для построения функции нужно только отрицание, поскольку прибавление двоичной константы либо ничего не изменяет, если она равна 0, либо меняет переменную на ее отрицание. Например, при , , .

В общем случае

Раскрыв скобки, убеждаемся, что . Таким образом, конъюнкция построена из функций системы .

Теорема доказана.

Для проверки полноты конкретной системы функций удобно заполнять таблицу, в которой отмечается 1 или 0 вхождение или невхождение функции в классы , , , и . Например, для системы функций

, где , ,

имеем следующую таблицу:

Таблица 2

Функция	Класс
	0	0	1	0	1
	1	1	0	1	0
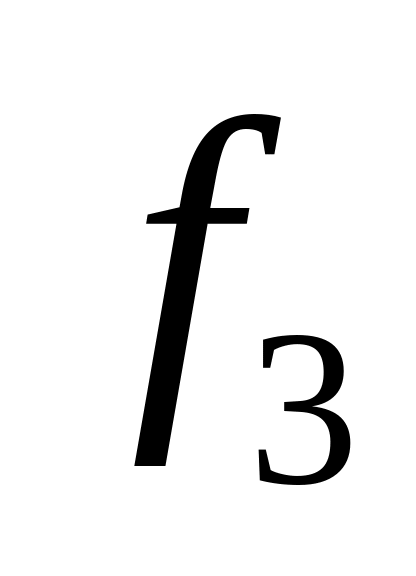
	1	1	0	1	0

Пример. Импликация имеет следующую таблицу истинности:

0 0	1
0 1	1
1 0	0
1 1	1

Из таблицы следует, что не сохраняет 0, несамодвойственна, немонотонна. Кроме того, , так как

.

Добавляя к любую функцию, не сохраняющую 1, получим полную систему. Рассмотрим, например, систему , где . Построим отрицание и конъюнкцию:

, при и имеем ;

.

Таким образом, для любой функции можно написать формулу, в которую будут входить только импликации и нули. Например,

.

13