
- •Определение булевой функции
- •Способы задания булевых функций
- •Формулы. Реализация функций формулами
- •Понятие суперпозиции
- •Эквивалентность формул. Основные тавтологии алгебры логики
- •Принцип двойственности
- •Разложение булевых функций по переменным. Совершенные
- •Полнота и замкнутость. Примеры функционально полных систем
- •Представление булевых функций полиномом Жегалкина
- •Класс функций, сохраняющий константу 0
- •Класс функций, сохраняющий константу 1
- •Класс самодвойственных функций
- •Класс линейных функций
- •Теорема Поста о полноте
- •Понятие днф. Проблема минимизации булевых функций
- •Геометрическая интерпретация задачи минимизации булевых функций
- •Определение тупиковой днф
- •Построение тупиковых днф методом упрощения совершенной днф
- •Определение сокращенной днф и геометрический метод ее построения
- •19.Минимизация булевых функций на основе построения тупиковых д. Н. Ф.
- •20. Минимизация булевых функций методом карт Карно.
- •21.Минимизация булевых функций методом Квайна-Мак-Класски
- •23.Задачи анализа и синтеза схем из функциональных элементов. Элементарные методы синтеза.
- •Элементарные методы синтеза
- •26 Синтез схем дешифратора и двоичного сумматора
- •28. Определение конечного автомата
- •Способы задания конечного автомата
- •29. Задача синтеза автоматов
- •Элементарные автоматы
- •Машина Тьюринга
- •Что собой представляет машина Тьюринга?
- •Пример работы машины Тьюринга
Класс самодвойственных функций
Обозначим через
класс всех самодвойственных функций
из
,
то есть таких, что
![]() .
.
Как и выше, нетрудно проверить, что добавление равных функций не выводит за пределы класса :
![]() .
.
Очевидно, что
самодвойственными будут функции
,
.
Менее тривиальным примером является
функция
![]() :
:
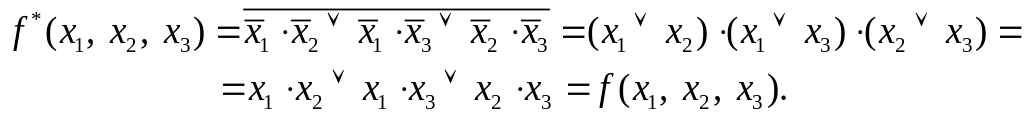
Для самодвойственной функции имеет место тождество
![]() .
.
Другими словами, на
противоположных наборах
и
![]() самодвойственная
функция принимает противоположные
значения. Отсюда следует, что
самодвойственная функция определяется
своими значениями на первой половине
строк таблицы истинности. Поэтому число
самодвойственных функций
переменных равно
самодвойственная
функция принимает противоположные
значения. Отсюда следует, что
самодвойственная функция определяется
своими значениями на первой половине
строк таблицы истинности. Поэтому число
самодвойственных функций
переменных равно
![]() .
.
Докажем, что класс замкнут, то есть, что суперпозиция самодвойственных функций является самодвойственной функцией. Для этого достаточно показать, что функция
![]()
является
самодвойственной, если
![]() самодвойственны. Последнее устанавливается
непосредственно:
самодвойственны. Последнее устанавливается
непосредственно:
![]() .
.
Докажем теперь лемму о несамодвойственной функции.
Лемма
2.
Если
![]() ,
то из нее путем подстановки функций
и
можно получить несамодвойственную
функцию одного переменного, то есть
константу.
,
то из нее путем подстановки функций
и
можно получить несамодвойственную
функцию одного переменного, то есть
константу.
Доказательство.
Так как
![]() ,
то найдется
набор
такой, что
,
то найдется
набор
такой, что
![]() .
.
Рассмотрим функции
![]() (
(![]() )
и положим
)
и положим
![]() .
.
Тогда
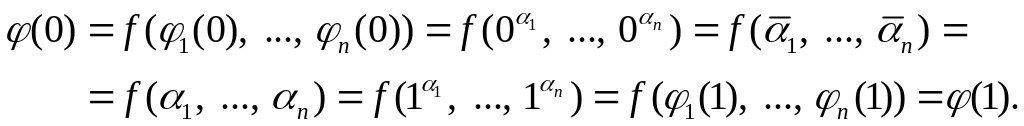
Лемма доказана.
Например, функция
несамодвойственна, так как
![]() .
Аналогично для функции
имеем:
.
Аналогично для функции
имеем:
![]() .
.
11
Класс линейных функций
Последним классом
является класс
![]() всех линейных функций.
всех линейных функций.
Функция называется линейной, если ее многочлен Жегалкина содержит только члены степени не выше первой:
![]() .
.
Класс
,
очевидно, содержит константы 0 и 1,
тождественную функцию
,
отрицание
,
сумму по mod
2
![]() .
Дизъюнкция
.
Дизъюнкция
![]() – нелинейная функция. Нелинейной также
является конъюнкция , многочлен Жегалкина
которого имеет вид
– нелинейная функция. Нелинейной также
является конъюнкция , многочлен Жегалкина
которого имеет вид
![]() .
.
Очевидным является следующее утверждение относительно замкнутости класса .
Лемма 5. Суперпозиция линейных функций является линейной функцией.
Докажем лемму о нелинейной функции.
Лемма
6.
Пусть
– нелинейная функция и
![]() .
Подстановкой констант на места
.
Подстановкой констант на места
![]() аргументов функции
можно получить нелинейную функцию от
двух аргументов.
аргументов функции
можно получить нелинейную функцию от
двух аргументов.
Доказательство. Рассмотрим многочлен Жегалкина функции , который по условию содержит, по крайней мере, один член степени выше первой. Переименовывая переменные, будем считать , что в этот член входят переменные , и, возможно, какие-то другие переменные. Выполним следующую группировку членов полинома Жегалкина функции : соберем члены, в которые входят и и вынесем за скобки. Среди оставшихся соберем члены, содержащие , и вынесем за скобки. Точно так же соберем члены, содержащие , и вынесем за скобки. В результате получим
![]() .
.
Здесь
![]() – некоторые функции от
– некоторые функции от
![]() ,
причем функция
тождественно
не равна 0. Это следует из единственности
полинома Жегалкина: если
тождественно
равно 0, то это означало бы, что функция
имеет два полинома Жегалкина – с
произведением
и без него. Тогда для некоторого набора
,
причем функция
тождественно
не равна 0. Это следует из единственности
полинома Жегалкина: если
тождественно
равно 0, то это означало бы, что функция
имеет два полинома Жегалкина – с
произведением
и без него. Тогда для некоторого набора
![]() значений переменных
имеем
значений переменных
имеем
![]() .
Отсюда
.
Отсюда
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
.
Лемма доказана.
В заключение заметим,
что замкнутые классы
![]() попарно
различны, что видно из следующей таблицы,
в которой знак + означает, что функция
содержится в классе, а знак – обозначает
противоположную ситуацию.
попарно
различны, что видно из следующей таблицы,
в которой знак + означает, что функция
содержится в классе, а знак – обозначает
противоположную ситуацию.
Таблица 1
-
0
+
–
–
+
+
1
–
+
–
+
+
–
–
+
–
+
12
