2. Способы задания булевых функций

Основными являются следующие способы представления булевых функций: табличный и аналитический.

Поскольку область определения состоит из конечного числа элементов ( ), то булеву функцию можно задать при помощи таблицы истинности (соответствия), в которой для каждого набора значений аргументов указывается значение функции (табл. 1).

Таблица 1. Таблица истинности булевой функции

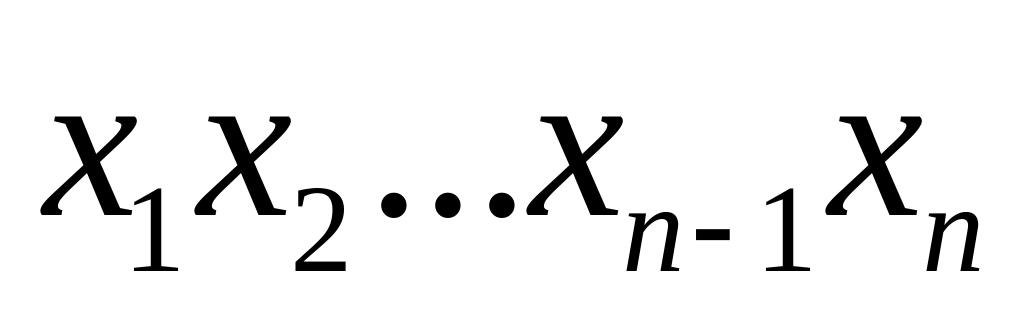
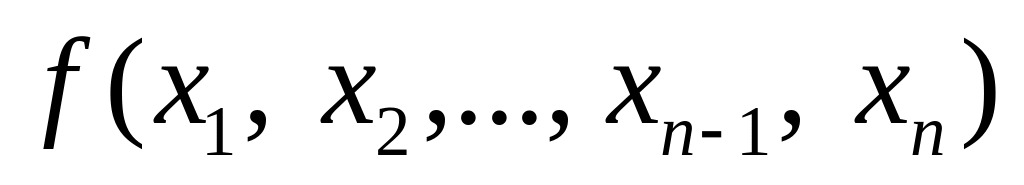
00…00
00…01
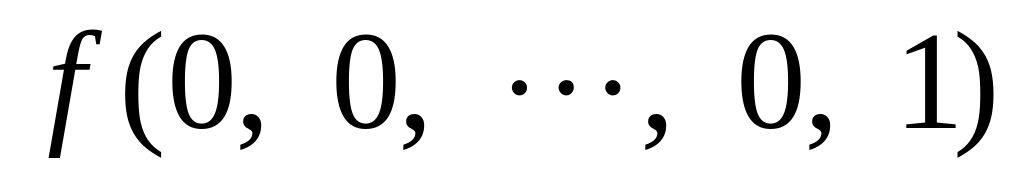
00…10
…	…
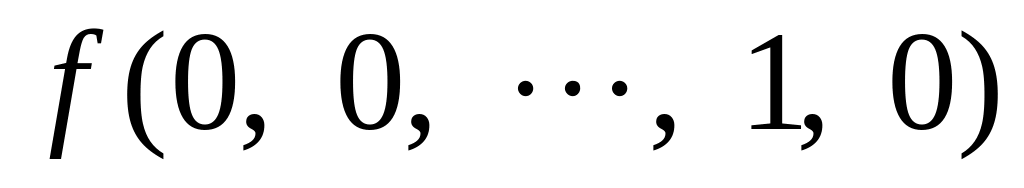
11…10
11…11

В качестве примера в таблице 2 задана функция от трех переменных, которая равна 1, нечетное количество переменных равно 1, и 0 – в остальных случаях.

Таблица 2. Пример задания булевой функции

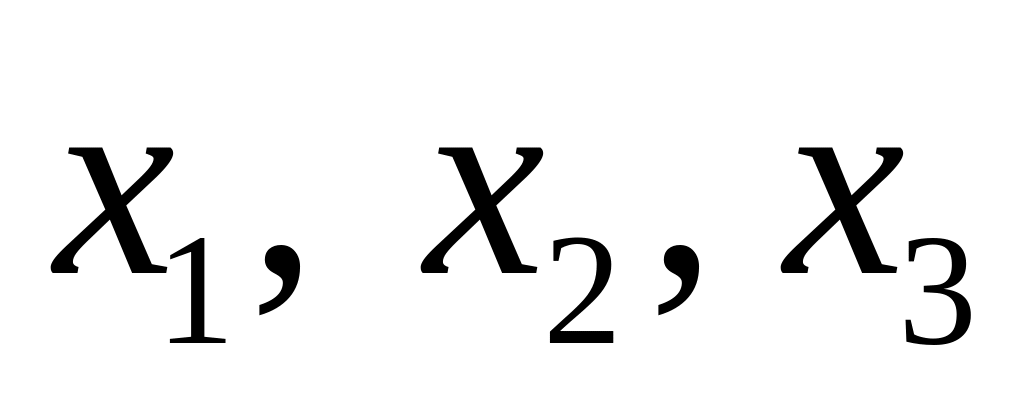
000	0
001	1
010	1
011	0
100	1
101	0
110	0
111	1

Отметим, что наборы значений аргументов в таблице записывают в естественной форме, то есть -ый по порядку набор представляет собой двоичную запись числа , =0, 1, 2, …, .

Обозначим через систему всех булевых функций от переменных. Число всех функций из равно числу перестановок с повторениями значений функции {0, 1} на выборке из входных наборов переменных, то есть .

Следует отметить, что числа с ростом быстро растут:

Следовательно, уже при сравнительно небольших значениях ( ) перебор функций из данного множества становится практически невозможен даже с использованием вычислительной техники. Кроме того, с ростом числа аргументов таблица истинности сильно усложняется. Так, например, уже при не очень большом числе аргументов, скажем при =10, таблица становится громоздкой (имеет 1024 строки), а при =20 – практически необозримой. Поэтому используют другие способы задания функции, среди которых основным является аналитический способ, то есть при помощи формул. При этом способе некоторые функции выделяются и называются элементарными, а другие функции строят из элементарных с помощью суперпозиции. Такой способ задания функции хорошо известен в математическом анализе. Например, функция построена суперпозицией многочлена , квадратного корня, косинуса и функции .

2

1. Формулы. Реализация функций формулами

В булевой алгебре, как и в элементарной алгебре, можно строить формулы, исходя из элементарных функций. Ниже приводится индуктивное определение формул.

Пусть – некоторое подмножество функций из .

а) Базис индукции. Каждая функция называется формулой над .

б) Индуктивный переход. Пусть – функция из и – выражения, являющиеся либо формулами над , либо символами переменных из исходного алфавита переменных .Тогда выражение называется формулой над .

Пример 1. Пусть – множество элементарных функций. Следующие выражения являются формулами над :

1. ;

2. ;

3. .

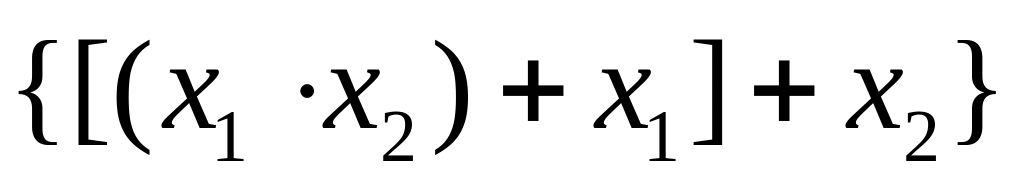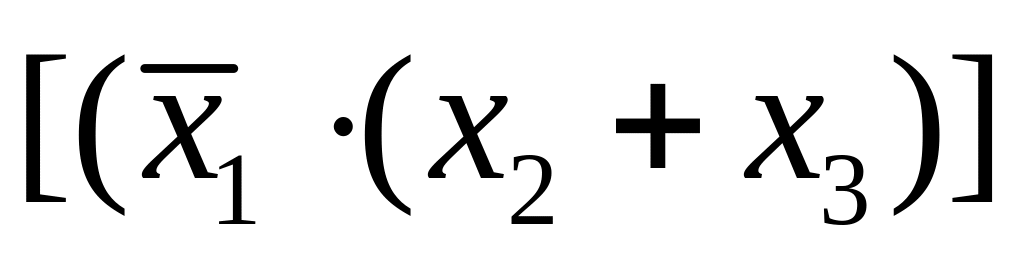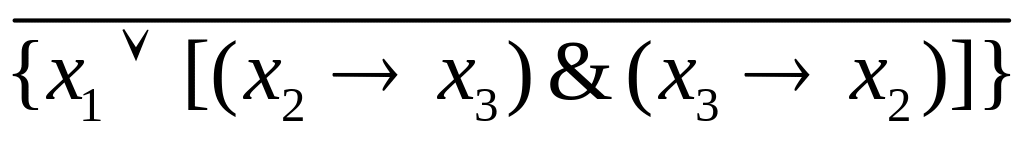Далее будем обозначать формулы заглавными буквами с квадратными скобками, в которых перечисляются функции, необходимые для их построения. Так означает, что формула построена из функций . В тех случаях, когда нужно обратить внимание на множество тех переменных, которые участвуют в построении формулы, пишут .

Пусть – произвольная формула над , тогда формулы, которые использовались для ее построения, будем называть подформулами формулы .

Пусть является формулой над множеством . Возьмем множество функций .

Рассмотрим формулу , которая получается из путем подстановки . Говорят, что формулы и имеют одно и то же строение.

Пример 2. Следующие формулы и имеют одинаковое строение:

1. , ;

2. , .

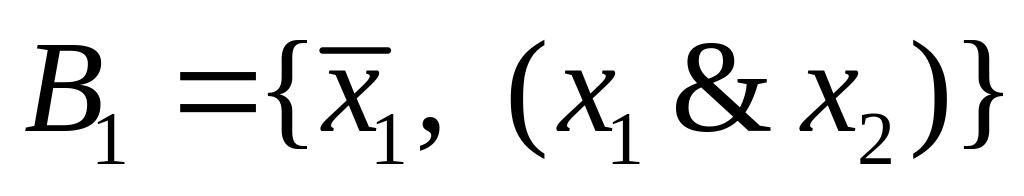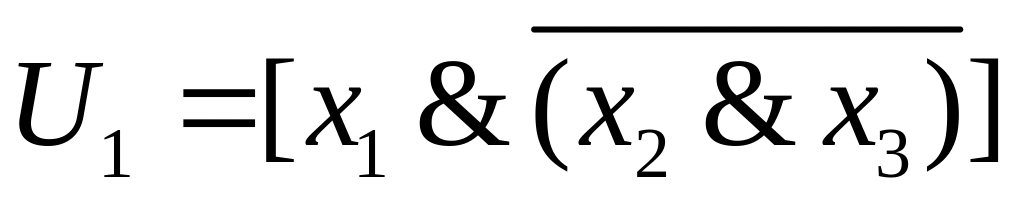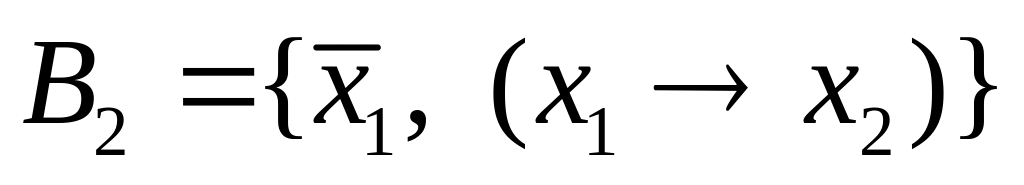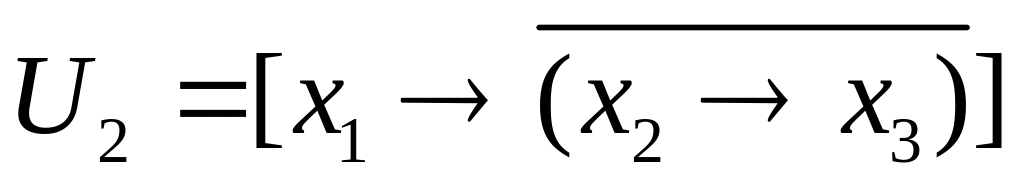Строение формулы обозначается через и формула однозначно определяется строением и упорядоченной совокупностью . Поэтому можно писать

.

Сопоставим теперь каждой формуле над функцию из , опираясь на индуктивное определение формул.

а) Базис индукции. Если , где , то формуле сопоставим функцию .

б) Индуктивный переход. Пусть , где является либо формулой над , либо символом переменной . Сопоставим формуле функцию .

Если функция соответствует формуле , то говорят также, что формула реализует функцию .

Введенное ранее понятие булевой функции не позволяет рассматривать функции от меньшего числа аргументов как функции от большего числа переменных. Для устранения этого недостатка введем следующее определение.

Функция зависит существенным образом от аргумента , если существуют такие значения переменных , что

.

В этом случае называется существенной переменной . В противном случае – несущественной или фиктивной.

Функции и называются равными, если функцию можно получить из путем добавления или изъятия фиктивных аргументов.

Поскольку функции рассматриваются с точностью до фиктивных переменных, то формула реализует любую функцию, равную .

3