1. Класс функций, сохраняющий константу 0

Обозначим через класс всех булевых функций из , сохраняющих константу 0, то есть функций, которые равны нулю на нулевом наборе переменных:

.

Заметим, что если , а , то и .

Легко убедиться, что функции 0, , , , принадлежат классу , а функции 1, , , не входят в .

Поскольку таблица для функции из класса в первой строке содержит значение 0, то в содержится ровно булевых функций от переменных.

Покажем, что – замкнутый класс. Для этого надо доказать следующее утверждение.

Лемма 1. Суперпозиция функций из класса является функцией класса .

Для доказательства необходимо убедиться, что применение операций и к функциям, сохраняющим 0, всякий раз дает функцию, сохраняющую 0.

В результате операции для функции имеем формулу , которая при нулевых значениях своих аргументов совпадает с .

Теперь покажем, что функция , полученная в результате применения операции , принадлежит , если принадлежат :

.

Лемма доказана.

Пример 1. Функции и входят в , поэтому суперпозиция этих функций будет сохранять 0. Следовательно, система неполная.

2. Класс функций, сохраняющий константу 1

Обозначим через класс всех булевых функций из , сохраняющих константу 1, то есть функций, которые равны 1 на единичном наборе переменных:

.

Например, функции 1, , , принадлежат классу , а функции 0, , не входят в .

В силу того, что класс двойствен классу , нетрудно перенести результаты о классе на класс . Так, если , а , то и . Класс содержит булевых функций от переменных и является замкнутым классом, то есть суперпозиция функций из класса является функцией класса .

Класс монотонных функций

Рассмотрим множество двоичных слов длины . Зададим на этом множестве отношение порядка (предшествования) следующим образом: будем говорить, что слово

предшествует слову

,

если

.

Тот факт, что слово предшествует слову будем обозначать .

Отношение предшествования удовлетворяет аксиомам рефлексивности, антисимметричности и транзитивности.

Например, 00 10 11, 0010 0111 1111.

Слова 01 и 10 не находятся в отношении предшествования. Такие слова называются несравнимыми.

Отношение “ ” можно представить в виде ориентированного графа. Для имеем следующий граф:

111

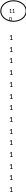
Рис. 1. Представление отношения предшествования в виде ориентированного графа

Слово предшествует слову , если от к можно пройти по стрелкам.

Функция называется монотонной, если для любых наборов переменных и выполняется условие

,

то есть значение функции на меньшем наборе не превосходит значения функции на большем наборе.

Очевидно, что функция, равная монотонной функции, также является монотонной.

Например, монотонными функциями будут 0, 1, , , .

Обозначим через множество всех монотонных функций. Покажем, что класс монотонных функций замкнут.

Лемма 3. Суперпозиция функций из класса является функцией класса .

Доказательство. Доказательство леммы проведем на примере конкретной суперпозиции, рассуждение для общего случая будет аналогичным.

Пусть , где . Покажем, что . Рассмотрим два сравнимых набора значений аргументов функции :

.

Тогда , и в силу монотонности имеет место неравенство

.

Отсюда и в силу монотонности имеет место неравенство

.

В результате имеем

Таким образом, . Лемма доказана.

Будем называть наборы и соседними по -ой координате , если

, .

Докажем теперь лемму о немонотонной функции.

Лемма 4. Из немонотонной функции путем подстановки констант на места некоторых аргументов можно получить отрицание.

Доказательство. Пусть . Это значит, что

.

Покажем, что для функции найдется пара соседних наборов, для которых нарушается условие монотонности. Очевидно, пару соседних наборов и , для которых , всегда можно связать цепочкой соседних наборов. Возьмем пару соседних наборов , , для которых

, .

Рассмотрим функцию одного аргумента

.

Имеем

.

Так как , а , то . Лемма доказана.

10