21.Минимизация булевых функций методом Квайна-Мак-Класски

Данный метод основывается на представлении элементарных конъюнкций, входящих в совершенную ДНФ данной функции, в виде двоичных чисел, называемых номерами соответствующих наборов. Кроме номера, каждой элементарной конъюнкции присваивается определенный индекс, равный числу единиц в двоичном представлении данного набора. Например:

элементарная конъюнкция (набор ) ; номер 010(2); индекс 1;

элементарная конъюнкция (набор ) ; номер 110(6); индекс 2.

В результате реализации данного метода функция разлагается на простые импликанты. Алгоритм Квайна-Мак-Класски формулируется следующим образом: для того, чтобы два числа и являлись номерами двух склеивающихся между собой наборов, необходимо и достаточно, чтобы индексы данных чисел отличались на единицу, сами числа отличались на степень числа 2 и число с большим индексом было больше числа с меньшим индексом.

Пример 2. Реализацию алгоритма рассмотрим на примере минимизации функции

.

На первом этапе минимизации определяем номера и индексы каждого набора, записывая функцию в виде

.

На втором этапе группируем наборы, располагая их в порядке возрастания индексов (табл. 1).

Таблица 1. Минимизация ФАЛ методом Квайна-Мак-Класски

Индекс	Номер	Результаты склеивания
I	0001(1)	00-1 0-01 -001	0--1 -0-1 0--1 -0-1
II	0011(3) 0101(5) 1001(9)	0-11 -011 01-1 10-1
III	0111(7) 1011(11)

На третьем этапе производим склеивание различных наборов, руководствуясь приведенной выше формулировкой алгоритма. При склеивании не совпадающие в числах разряды отмечаются прочерками. Например, склеивание чисел 0001 и 0011 дает число 00-1. Результат склеивания записывается в следующий столбец таблицы 1, также разделяемый на строки с индексами, отличающимися на единицу. После склеивания всех групп первого столбца таблицы переходят ко второму, записывая результат склеивания в третий столбец. При объединении второго и последующих столбцов таблицы возможно склеивать только числа, содержащие прочерки в одноименных разрядах. Склеивание продолжается до тех пор, пока образование нового столбца станет невозможно.

На четвертом этапе после окончания склеивания приступают к построению импликантной таблицы (табл. 2), записывая в нее в качестве простых импликант наборы, содержащиеся в последнем столбце таблицы 1. В таблицу 2 также вписываются в качестве простых импликант наборы из других столбцов таблицы 1, не принимавшие участия в склеивании. Если импликанта, содержащаяся в -ой строке таблицы, составляет часть конституенты -го столбца, то на пересечении -ой строки и -го столбца ставится символ *. Для получения минимальной формы ФАЛ из таблицы 2 необходимо выбрать минимальное число строк, чтобы для каждого столбца среди выбранных строк нашлась хотя бы одна, содержащая в этом столбце символ *.

Таблица 2. Импликантная таблица минимизируемой функции

Импликаты	Наборы
	*	*		*		*
	*		*		*	*

В результате минимизации функция представится в виде

.

22. Понятие схемы из функциональных элементов. Структурная и функциональная части понятия. Реализация булевых функций схемами.

В современной технике управляющих и вычислительных устройств важное место занимают дискретные преобразователи, т. е. устройства, которые обладают некоторым числом входов и выходов. Наборы сигналов, поступающие на входы и возникающие на выходах, принадлежат известным конечным множествам. Устройства осуществляют преобразования входных наборов сигналов в выходные. Математической моделью таких устройств являются так называемые схемы из функциональных элементов (СФЭ).

Определение понятия СФЭ можно разбить на два этапа. На первом этапе раскрывается структурная часть этого понятия, на втором – функциональная.

I этап. Разобьем этот этап на ряд пунктов.

1. Имеется конечное множество объектов ( ), называемых логическими элементами. Каждый элемент имеет входов и один выход. Элемент графически изображается так, как указано на рис. 2.

2. По индукции определяем понятие логической сети как объекта, в котором имеется некоторое число входов и некоторое число выходов (рис. 3).

а) Базис индукции. Изолированная вершина называется тривиальной логической сетью. По определению, она является одновременно входом и выходом (рис. 4).

… …



…

Рис. 2 Рис. 3 Рис. 4

б) Индуктивный переход. Эта часть основана на использовании трех операций.

I. Операция объединения непересекающихся сетей. Пусть и – две непересекающиеся сети (без общих элементов, входов и выходов), имеющие соответственно и входов и и выходов. Теоретико-множественное объединение сетей и есть логическая сеть , которая имеет входов и выходов.

II. Операция присоединения элемента . Пусть сеть и элемент таковы, что и в выбрано различных выходов с номерами . Тогда фигура называется логической сетью, являющейся результатом подключения элемента к сети . Входами являются все входы , выходами – все выходы сети , кроме выходов с номерами , а также выход элемента . Сеть имеет входов и выходов (рис. 5).

… …

Рис. 6.

Рис. 5

III. Операция расщепления выхода. Пусть в сети выделен выход с номером . Тогда фигура называется логической сетью, полученной путем расщепления выхода . Входами являются все входы , выходами – все выходы сети с номерами 1, …, , , …, и еще два выхода, возникших из выхода с номером сети (рис. 6). Следовательно, имеет входов и выходов.

3. Пусть заданы алфавиты и .

Схемой из функциональных элементов называется логическая сеть с входами из алфавита и выходами из алфавита , которая обозначается

. (1)

Приведем примеры схем.

1. Пусть множество состоит из трех элементов И (конъюнктора), ИЛИ (дизъюнктора) и НЕ (инвертора).

Тогда фигура (рис. 6) будет схемой, так как она может быть построена с использованием операций I–III.

 

Рис. 6 Рис. 7

2. Фигура, изображенная на рис. 7, будет также схемой.

II этап. Определение функционирования схемы.

4. Сопоставим СФЭ (1) систему функций алгебры логики

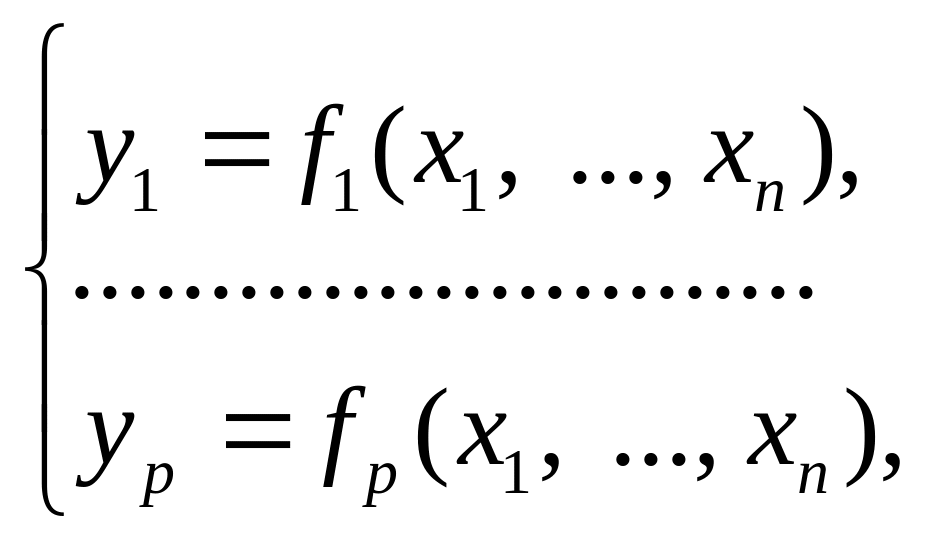(2)

называемую также проводимостью данной схемы.

Пример. а) Для схемы имеем систему, состоящую из одного уравнения

или .

б) Для схемы аналогично получаем

.

Реализация булевых функций схемами из ФЭ. Задачи анализа и синтеза

схем из ФЭ

Задача анализа: для данной СФЭ (1) получить систему булевых уравнений (2).

Алгоритм решения задачи: следуя операциям построения сети I – III, последовательно вычисляем функции на выходах элементов сети.

Задача синтеза: для данного базиса функциональных элементов и произвольной системы булевых уравнений (2) построить схему (1) из заданных ФЭ, реализующую эту систему уравнений.

Существование решения задачи синтеза определяется теоремой Поста, согласно которой система функций , реализующих базисные ФЭ, должна быть полна. Функции можно представить в виде суперпозиции функций , а каждому шагу суперпозиции соответствует определенное соединение элементов.

Пример. Для функции

(3)

Схема, соответствующая суперпозиции в правой части формулы (3), показана на рис. 8.

  

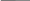
Рис. 8

Проблема синтеза заключается в том, что для данной системы булевых уравнений можно построить много схем из ФЭ, которые реализуют эту систему. В связи с этим возникает задача оптимального синтеза: из всевозможных схем, реализующих данную функцию, выбрать наилучшую по тому или иному признаку, например, с наименьшим числом элементов. Такие схемы будем называть минимальными.

Справедливо следующее утверждение.

Теорема. Существует алгоритм, который для каждой системы булевых функций строит минимальную схему .

Данный алгоритм построения минимальных схем относится к классу алгоритмов типа «полного перебора», так как он основан на просмотре всех схем до определенной сложности. Алгоритмы полного перебора, как правило, обладают большой трудоемкостью и непригодны для практических целей. Поэтому рассмотрим далее более простую задачу, для которой исходная система уравнений содержит одно уравнение

,

и, следовательно, искомая схема имеет один выход.

Сложность минимальной схемы обозначим через . Будем рассматривать задачу синтеза не для отдельной функции , а для всего класса функций от переменных. Качество алгоритмов синтеза сравнивается путем сопоставления так называемых функций Шеннона. Пусть

, ,

– минимальная сложность схем, реализующих , которые получаются при помощи алгоритма .

Функции , называются функциями Шеннона, причем очевидно, что

.

Задача синтеза состоит в том, чтобы найти алгоритм , для которого была бы воз можно ближе к , и чтобы трудоемкость алгоритма была бы существенно меньше, чем трудоемкость алгоритма полного перебора. При такой постановке задачи не требуется, чтобы алгоритм для каждой функции находил минимальную схему, необходимо только, чтобы простейшая схема, получаемая при помощи , имела сложность , сильно не превышающую .