
- •1. Теорема Вейерштрасса о пределе монотонной последовательности.
- •2. Понятие вектора. Линейные операции над векторами и их св-ва.
- •1. Эквивалентность определений предела функции по Коши и Гейне.
- •1. Основные свойства предела функции.
- •1.Сумма, произведение, частное и композиция непрерывных функций.
- •2. Симметрические многочлены от нескольких переменных. Основная теорема о симметрических многочленах. Формулы Виета.
- •1. Свойства функций непрерывных на отрезке.
- •2. Векторное ум. Двух векторов трёхмерного евклидового пространства, его свойства и применение к решению задач
- •Геометрические свойства
- •Алгебраические свойства
- •1. Производная суммы, произведения, частного и композиции функции. Произв. Обратной функ.
- •2. Система аксиом плоскости Лобачевского,д-во ее непротиворечивости.
- •1. Основные теоремы дифференциального исчисления.
- •2. Смеш. Произ. 3 в-ров 3-х мерного Евклидова пр-ва. Его св-ва и прим. К реш. Геомет. Задач.
- •1. Необходимые и достаточные условия возрастания и убывания функции.
- •2. Многочлены от одной переменной над полем действительных чисел. Сопряженность мнимых корней, описание неприводимых многочленов.
- •1. Необходимые и достаточные условия локального экстремума функции.
- •2. Прямая на плоскости как линия первого порядка.Взаим.Распол. Двух прямых.
- •Различные способы задания прямой (направляющим вектором и точкой) и соответствующие им уравнения.
- •Взаимное расположение 2-х прямых на плоскости, заданных общими уравнениями.
- •1. Линейные св-ва опред.Интеграла и св-ва,связанные с неравенствами.
- •Линейные свойства интеграла Римана.
- •Свойства, связанные с неравенствами.
- •1. Достаточное условие существования определенного интеграла.
- •2. Эллипс,гипербола,парабола. Вывод канон.Ур-ия, изучение формы.
- •1. Теорема дифференц. Опред. Интеграла по верхнему пределу.Формула Ньютона-Лейбница.
- •2. Отношение делимости в кольце многочленов от одной переменной над полем. Нод двух многочленов. Алгоритм Евклида.
- •2. Плоскость как поверхность первого порядка. Взаимное расположение двух плоскостей.
- •7.3. Взаимное расположение двух плоскостей.
- •2. Отношение сравнения целых чисел, свойства. Сравнения первой степени.
- •1. Необходимые и достаточные условия дифференцируемости ф-ций комплексной переменной. Понятие аналитической ф-ции в точке и в области.
- •Счетность множества рациональных чисел.
- •1. Несчетность множества точек отрезка [ 0,1 ]
- •2. Кольцо классов вычетов, приведённая система классов вычетов.
- •1. Скалярное умножение двух векторов трехмерного евклидова пространства, его свойства и применение к решению геометрических задач.
- •2. Неприводимые многочлены над полем. Разложение многочлена в произведения неприводимых множителей и его единственность над полем.
- •1. Векторные пространства, простейшие свойства, примеры векторных пространств. Подпространства.
- •Применение гомотетии (подобия) к решению задач на построение (или на доказательство).
- •Классиф. Движений первого рода плоскости, их применение к решению задач по геометрии.
- •2. Простые и составные числа. Бесконечность мн-ва простых чисел.
- •1. Тригон. Форма комп. Числа. Формула Муавра. Корни n – ой степени из комплексного числа.
- •1.Классификация движений второго рода плоскости, их применение к решению геом. Задач.
- •2. Системы линейных ур-ий, их виды. Равносильные системы линейных ур-ий. Метод исключения неизвестных, критерий совместности и неразрешимости.
- •2. Изображение пространственных фигур в параллельной проекции.
- •2.Взаимное расположение двух прямых на плоскости Лобачевского.
- •2. Изображение плоских фигур в параллельной проекции.
- •14 Вопрос. Проективная плоскость (пп) и ее модели.
- •19. Кривизна и кручение кривой в трехмерном евклидовом пространстве.
1. Достаточное условие существования определенного интеграла.
Теорема1 Если f(x)интегрируема
на отрезке [a;b],
то она ограничена на [a;b].
(Необходимый признак интегрируемости
ф-ии, обратное неверно)След-ие Если
f(x) неогранич.
на отрезке [a;b]
то f(x) не
интегр-ма на отрезке [a;b].
Пусть f(x)
определена и ограничена на[a;b],
разобъем [a;b]
на n частичных отрезков
a=x0<x1<x2<…<xk-1
< xk<…<xn=b.Положим
Мк=supE(f),
mk=infE(f)
на [хк-1,хк] Эти грани
существуют. Если числовое множество
ограничено сверху, то оно имеет точную
верхнюю грань, а если снизу, то точную
нижнюю грань.Опр.
![]() ,
,
![]() наз-ся
верхней и нижней интегр-ой суммами или
верхней и нижней суммами Дарбу. Эти
суммы зависят только от разбиения. Они
похожи на обычные интегральные суммы
наз-ся
верхней и нижней интегр-ой суммами или
верхней и нижней суммами Дарбу. Эти
суммы зависят только от разбиения. Они
похожи на обычные интегральные суммы
![]() ,
но вообще не являются частным случаем
обычной интегральной суммы, т.к. числа
Мк и mk
могут не быть значениями ф-ии. Но в
частном случае, когда ф-ия непрерывна
на [a,b] они
являются частными случаями обычной
интегральной суммы, т.к. если ф-ия
непрерывна на [a,b],
то она имеет на ней наибольшее и наименьшее
значение (Теорема Больцано-Вейерштрассе).Теорема2:
Для того чтобы f(x)
была интегрируема на [a,b]
необходимо и достаточно, чтобы
,
но вообще не являются частным случаем
обычной интегральной суммы, т.к. числа
Мк и mk
могут не быть значениями ф-ии. Но в
частном случае, когда ф-ия непрерывна
на [a,b] они
являются частными случаями обычной
интегральной суммы, т.к. если ф-ия
непрерывна на [a,b],
то она имеет на ней наибольшее и наименьшее
значение (Теорема Больцано-Вейерштрассе).Теорема2:
Для того чтобы f(x)
была интегрируема на [a,b]
необходимо и достаточно, чтобы
![]() (без док-ва критерий интегрируемости
по Риману)Теорема3 Если
f(x)непрерывна
на отрезке [a;b],
то f(x)интегрируема
на отрезке [a;b].(можно
д-ть Т4,а можно Т3).
(без док-ва критерий интегрируемости
по Риману)Теорема3 Если
f(x)непрерывна
на отрезке [a;b],
то f(x)интегрируема
на отрезке [a;b].(можно
д-ть Т4,а можно Т3).
Док-во: Если ф-ия Х непрерывна на отрезке,
то она равномерно непрерывна на этом
отрезке (теорема Кантора о равномерной
непрерывности
![]()
![]()
![]()
![]()
Здесь δ зависит только от ε и следовательно
число δ обслуживает все пары точек х’
и x” из Х. В данном сл. роль
Х играет [a;b].
![]() ,
если
,
если
![]() Т.к.
Мк и mк являются
значениями ф-ии на [xk-1,xk]
в силу непрерывности ф-ии, то
Т.к.
Мк и mк являются
значениями ф-ии на [xk-1,xk]
в силу непрерывности ф-ии, то
![]() такие,
что f(xk’)=Mk,
f(xk”)=
mkТогда
такие,
что f(xk’)=Mk,
f(xk”)=
mkТогда
![]() Применим
для
Применим
для
![]()
![]() если
если![]() т.е.
т.е.
![]()
Вернемся к S-s. Вместо |xk’-x”k|<δ можно писать λ<δ
![]()
Отсюда следует
![]() по
Т2 f(x)
интегрируема на [a;b]
по
Т2 f(x)
интегрируема на [a;b]
Теорема4 Если f(x) монотонна и ограничена на [a;b] , то она интегрируема на [a;b]
↓Пусть ![]() явл.неубывающей. Это значит, что
явл.неубывающей. Это значит, что![]() ,
т.е.
-
ограничена на
,
т.е.
-
ограничена на ![]() вып.необходимое
условие интегрируемости: если
интегрир.на
,
то она ограничена на этом отрезке. Пусть
вып.необходимое
условие интегрируемости: если
интегрир.на
,
то она ограничена на этом отрезке. Пусть
![]() -
произв.разбиение
с диаметром разбиения d.
Тогда на каждом частичном отрезке
-
произв.разбиение
с диаметром разбиения d.
Тогда на каждом частичном отрезке![]() Тогда
Тогда
![]() Возьмем
произв.
Возьмем
произв.![]() и определим
и определим
![]() ;
;
![]() .
В силу критерия интегрир.по Риману это
означает, что
– интегрируема. ↑Теоремы 3,4 являются
только достаточными признаками
интегрируемости функции, т.к. предложения
обратные Т3 и Т4 не верны: теорема обратная
Т3- потому что верна Т4, и теорема обратная
Т4 – потому что верна Т3.
.
В силу критерия интегрир.по Риману это
означает, что
– интегрируема. ↑Теоремы 3,4 являются
только достаточными признаками
интегрируемости функции, т.к. предложения
обратные Т3 и Т4 не верны: теорема обратная
Т3- потому что верна Т4, и теорема обратная
Т4 – потому что верна Т3.
2. Эллипс,гипербола,парабола. Вывод канон.Ур-ия, изучение формы.
п.1. Определения эллипса, гиперболы, параболы.
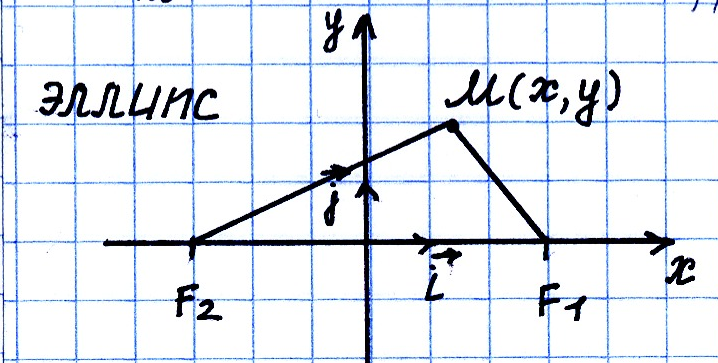
• Эллипсом называют множество всех
тех точек плоскости, для каждой из
которых сумма расстояний до 2-х данных
точек
![]() и
и
![]() есть
величина постоянная, большая, чем
расстояние между
и
.
Элементы : Точки
и
называются фокусами, а
есть
величина постоянная, большая, чем
расстояние между
и
.
Элементы : Точки
и
называются фокусами, а
![]() - фокальным расстоянием. Обозначим
через
- фокальным расстоянием. Обозначим
через
![]() сумму
расстояний от любой точки эллипса до
фокусов, а через
сумму
расстояний от любой точки эллипса до
фокусов, а через
![]() .
По определению
.
По определению
![]() .
Уравнение:
.
Уравнение:
![]()
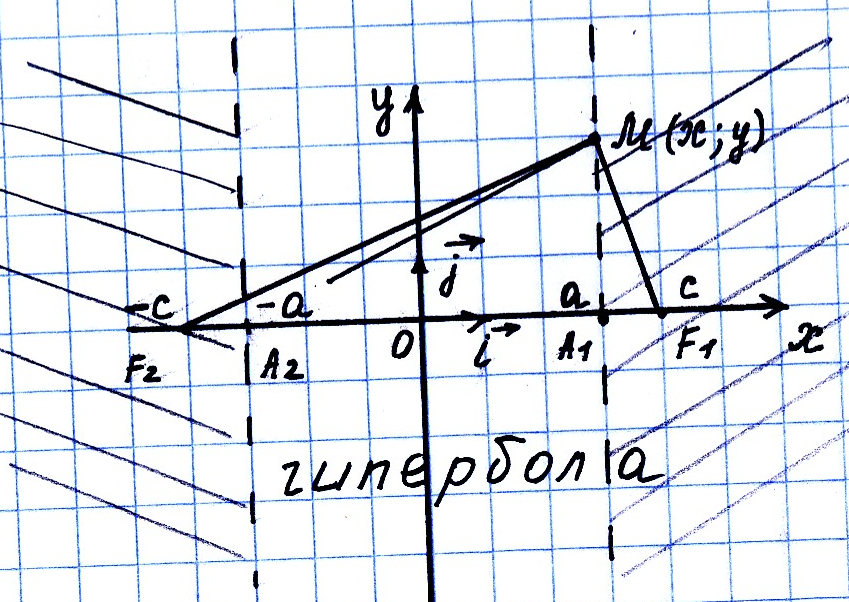
• Гиперболой называется множество
всех тех точек плоскости, для каждой из
которых модуль разности расстояний до
2-х данных точек
и
- есть величина постоянная, меньшая, чем
расстояние между
и
.
Обозначим через
модуль
разности от любой точки гиперболы до
фокусов, а через
.
По определению
![]() .
Уравнение:
.
Уравнение:
![]() .
.
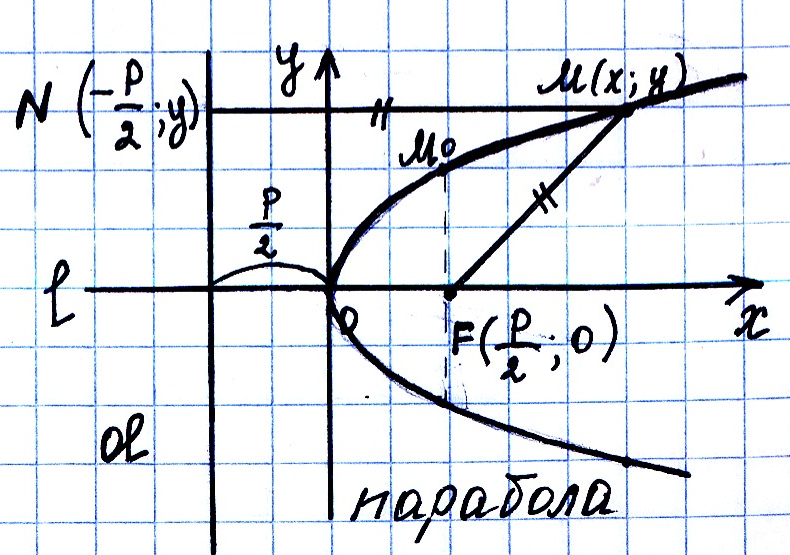
• Параболой называется множество
всех тех точек плоскости, для каждой
из которых расстояние до данной точки
![]() равно
расстоянию до данной прямой
равно
расстоянию до данной прямой
![]() ,
которая не проходит через
.
,
которая не проходит через
.
Элементы:
- фокус параболы,
- директрисса,
![]() - фокальный параметр параболы.
- фокальный параметр параболы.
Уравнение:
![]() .
.
п.2. Вывод канонического уравнения эллипса.
Обозначим через сумму расстояний от любой точки эллипса до фокусов, а через .
По определению
Найдем уравнение эллипса.
Выберем ПДСК (правая), начало координат т. О – середина
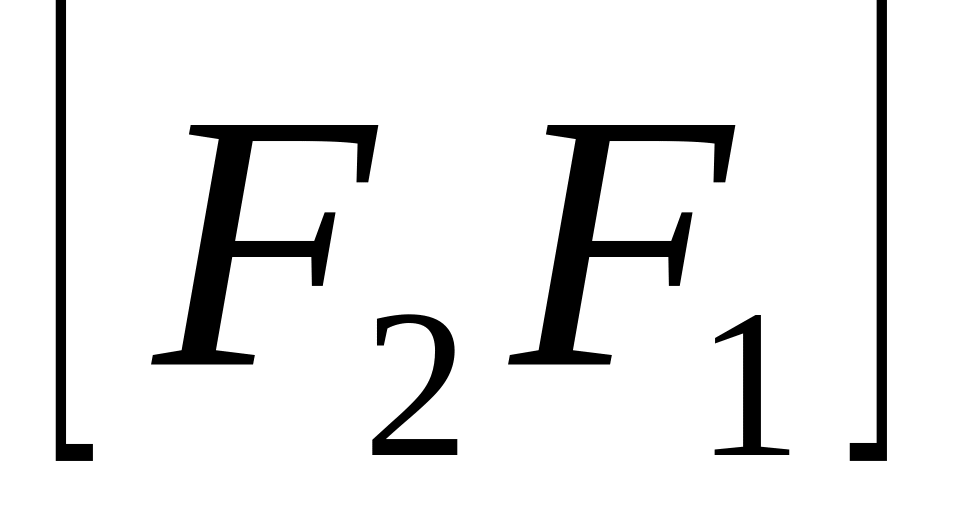 ,
ось Ох – прямая
,
,
ось Ох – прямая
,
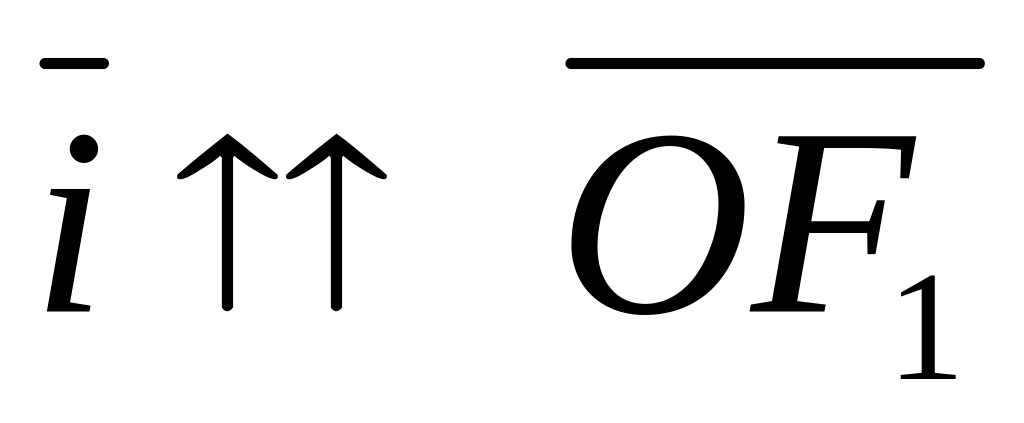 ,
,
 ,
,
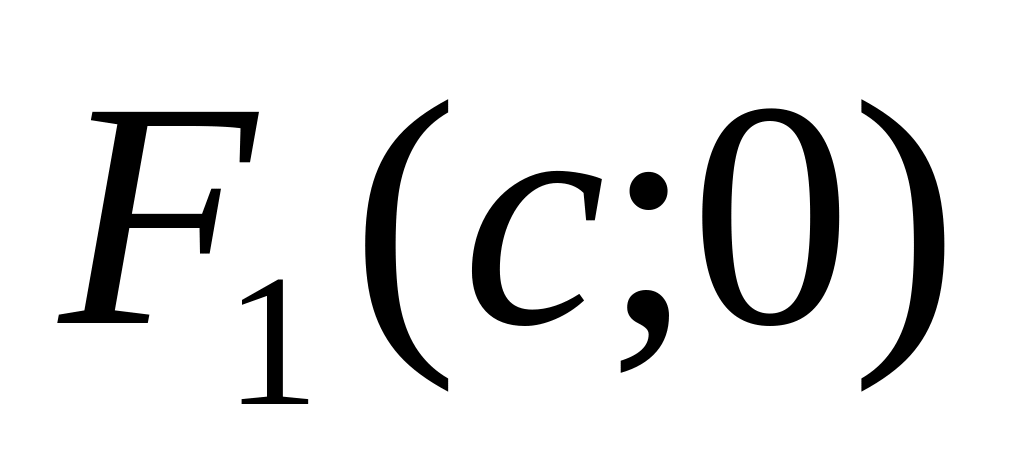 ,
,
 .
.
Пусть - текущая точка эллипса
 ,
т.е.
,
т.е.
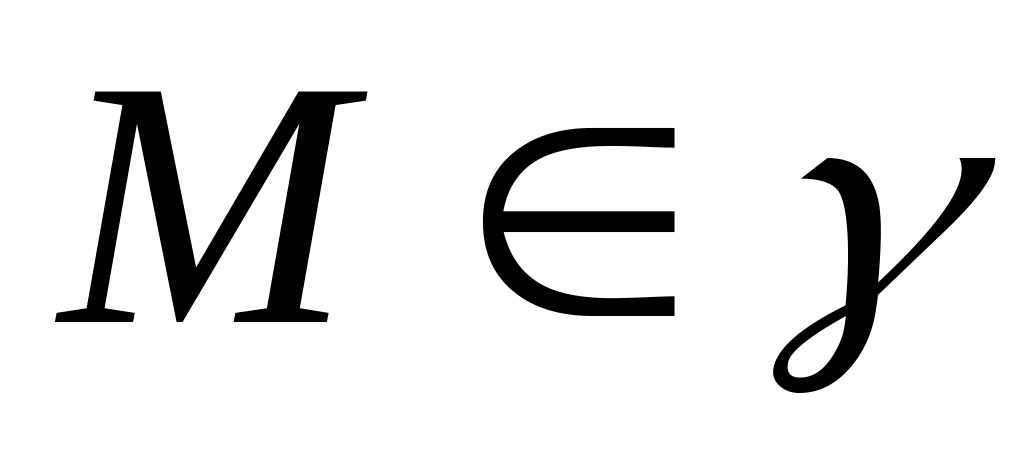 :
:
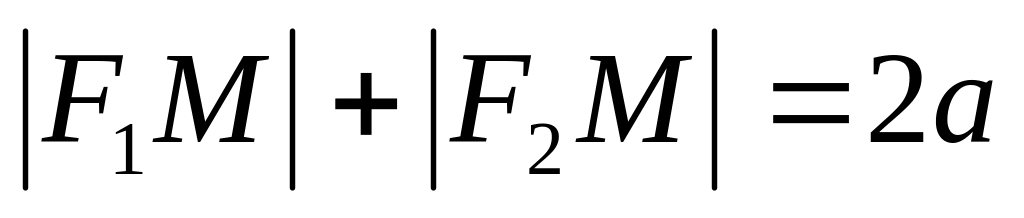 (*)
(*)Условие (*) записывается в координатах:
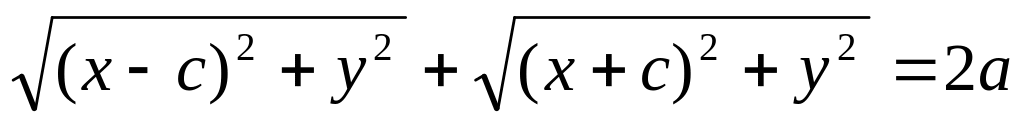 .
.Упростим полученное уравнение:
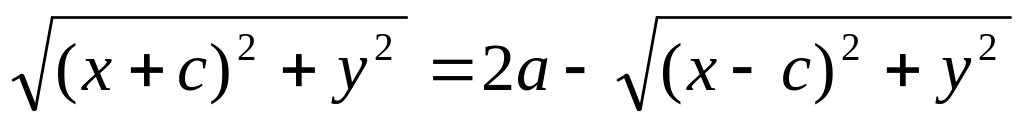
![]()
![]()
![]()
![]() возводим
в квадрат
возводим
в квадрат
![]()
![]()
![]() ,
введем обозначение:
,
введем обозначение:
![]()
![]() (1) – каноническое уравнение эллипса.
(1) – каноническое уравнение эллипса.
п.3. Изучение геометрических свойств линии по их каноническим уравнениям.
Эллипс:
1. Прохождение через начало координат:
т.
![]() т.к.
т.к.
![]()
2. Пересечение с осями:
![]()

![]()
![]()
![]() и
и
![]() .
.
![]()

![]() и
и
![]() .
.
• Точки пересечения с каноническими осями координат называются его вершинами.
•Числа а и b называются полуосями эллипса.
3. Симметричность. Т.к. переменные х и у входят в уравнение эллипса в четной степени, то эллипс симметричен относительно Ох и Оу. Эллипс так же симметричен относительно начала координат, т.к. при замене х на (-х) уравнение не изменится.
Гипербола:
1. Прохождение через начало координат:
т.
т.к.
![]()
2. Пересечение с осями:
 и
.
и
.
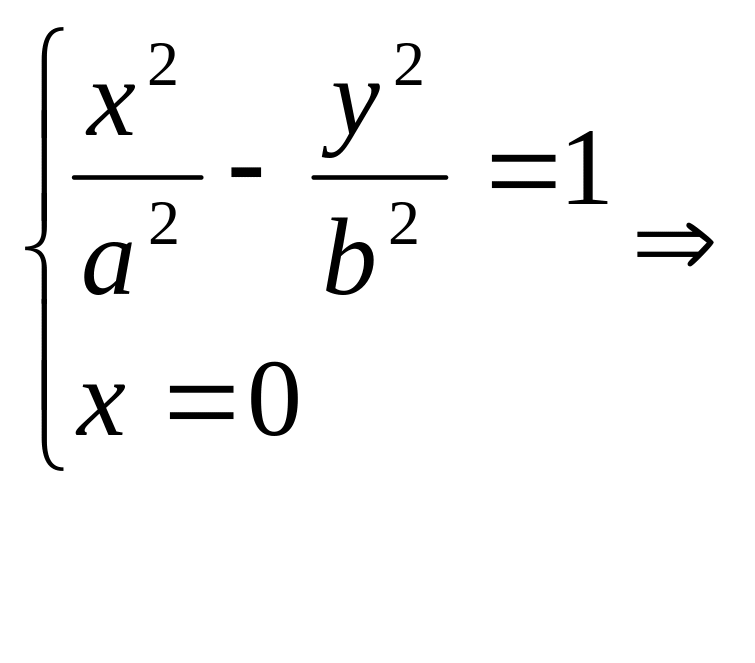 Решений нет, следовательно, и точек
пересечения с осью Oy.
Решений нет, следовательно, и точек
пересечения с осью Oy.
3. Симметричность. Т.к. переменные х
и у входят в уравнение гиперболы в
четной степени, то гипербола симметрична
относительно Ох и Оу. Эллипс так же
симметричен относительно начала
координат, т.к. при замене х на (-х)
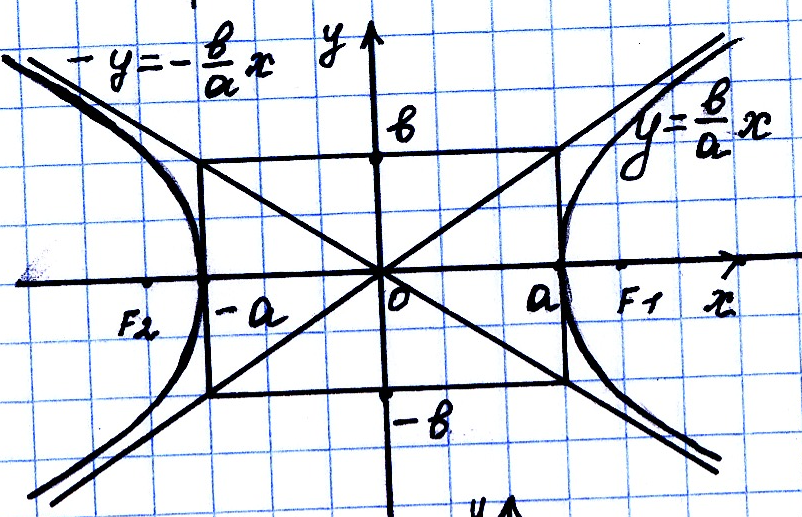
уравнение не изменится.4. Асимптоты
гиперболы – 2 прямые
![]() и
и
![]() .Выясним
расположение гиперболы относительно
асимптоты.
.Выясним
расположение гиперболы относительно
асимптоты.
![]() ,
,
![]() ,
очевидно, что
,
очевидно, что
![]() прямая
расположена выше гиперболы.
прямая
расположена выше гиперболы.
![]() при возрастании x уменьшается
при возрастании x уменьшается
![]() точки
гиперболы неограниченно приближаются
к асимптотам, не пересекая ее. В силу
симметричности теми же свойствами
обладает и вторая асимптота.
точки
гиперболы неограниченно приближаются
к асимптотам, не пересекая ее. В силу
симметричности теми же свойствами
обладает и вторая асимптота.
Парабола:
1. Прохождение через начало координат:
т.
![]() т.к.
т.к.
![]() .
.
2. Пересечение с осями: пересекает оси в начале координат - вершина.
3. Симметричность. Т.к. переменная у входит в уравнение параболы в четной степени, то парабола симметрична относительно Ох, но не симметрична относительно Оу и начала координат.
п.4. Изображение линии относительно канонической системы координат.
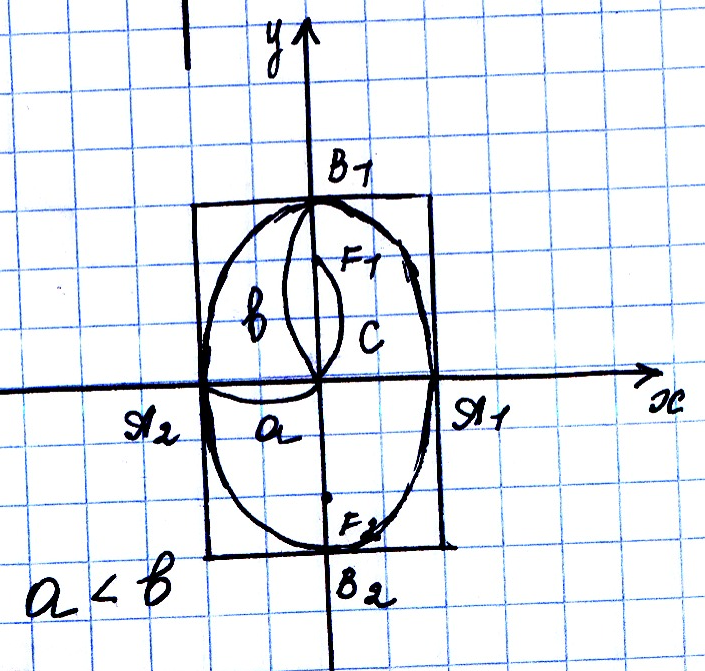
Эллипс: т.к. линия имеет 2 оси симметрии и цент симметрии, то для построения достаточно изображать часть линии, расположенной в 1 координатной четверти.
Из уравнения эллипса следует, что
![]() и
и
![]()
![]() и
и
![]()
![]()
![]() все точки эллипса лежат внутри
прямоугольника со сторонами 2а и 2b.
все точки эллипса лежат внутри
прямоугольника со сторонами 2а и 2b.
Из (1)
![]() . Для 1 четверти:
. Для 1 четверти:
![]() ,
если
,
если
![]() ,
,
![]() .
Т.о. при возрастании х от 0 до а, у убывает
от b до 0.
.
Т.о. при возрастании х от 0 до а, у убывает
от b до 0.
•Эксцентриситет - число, равное
![]() ,
где
,
где
![]() - большая полуось,
- большая полуось,
![]() .
.
Для эллипса
![]() .
.
![]() , т.е. эллипс сплющивается.
, т.е. эллипс сплющивается.
Директрисы эллипса – 2 прямые,
параллельные малой оси эллипса и
отстоящие от нее на расстояние
![]() .
.
![]() ,
т.к.
,
т.к.
![]() то
то
![]() ,
поэтому директрисы лежат вне эллипса.
,
поэтому директрисы лежат вне эллипса.
Гипербола: Если на оси Oy
отметить т.
и
т.
,
то -
![]() мнимая ось гиперболы ,
мнимая ось гиперболы ,
![]() - действительная ось гиперболы. Рассмотрим
прямоугольник со сторонами 2a
и 2b и с центром в начале
координат. При этом, диагонали
прямоугольника – асимптоты гиперболы.
- действительная ось гиперболы. Рассмотрим
прямоугольник со сторонами 2a
и 2b и с центром в начале
координат. При этом, диагонали
прямоугольника – асимптоты гиперболы.
Из уравнения гиперболы, следует, что
![]() .
Т.о. между
.
Т.о. между
![]() точек гиперболы нет, значит она состоит
из 2 ветвей.
точек гиперболы нет, значит она состоит
из 2 ветвей.
•Эксцентриситет - число, равное , где - действительная полуось,
Для гиперболы
![]() .
.
![]() ,
т.е. гипербола расширяется.
,
т.е. гипербола расширяется.
Директрисы гиперболы – 2 прямые,
параллельные ее мнимой оси и отстоящие
от нее на расстояние
.
т.к.
![]() то
то
![]() ,
следовательно директрисы расположены
внутри полосы, меджу x=a
и x=– a.
,
следовательно директрисы расположены
внутри полосы, меджу x=a
и x=– a.
Парабола:Выбираем ПДСК.
![]() т.
т.
![]() - середина
- середина
![]() ,
,
![]() ,
,
![]() ,
,
т.
![]() - текущая точка параболы,
- текущая точка параболы,
![]() ,
,
![]() .
.
Эксцентриситет параболы
![]() по
определению и в силу геометрического
смысла эксцентриситета
по
определению и в силу геометрического
смысла эксцентриситета
![]() для
для
![]() .
.
п.5. Связь темы со школьным курсом геометрии.
В школьном курсе изучается парабола, но с вертикальной осью симметрии, а также равносторонняя гипербола, как частный случай гиперболы. Окружность, как частный случай эллипса. В физ.-мат. классах изучаются все известные кривые.

Билет №12
