1. Линейные св-ва опред.Интеграла и св-ва,связанные с неравенствами.

Пусть дана функция на и пусть - разбиение на частичные отрезки : ^.

, - диаметр разбиения. В каждом из частичных отрезков выберем произвольную точку ; - интегральная сумма.

•Число I называется пределом интегральных сумм , когда ,если при любом выборе точек на частичных отрезках.

•Функция называется интегрируемой по Риману на , если , при этом I называется определенным интегралом Римана и обозначается .

(Определенным интегралом называется предел (предполагается, что он существует) интегральной суммы при стремлении к нулю длины наибольшего частичного интервала).

•Функция называется интегрируемой, если для нее существует определенный интеграл.

.

Линейные свойства интеграла Римана.

Если функции и интегрируемы на , то функции и , где , также интегрируемы на и 1) ; 2) .

↓1) Рассмотрим функцию на . . Перейдем к пределу слева и справа, когда . .↑

Свойства, связанные с неравенствами.

1) Если на и функция интегрируема на , то .

2) Если функции и интегрируемы на и на этом отрезке, то .

↓ Рассмотрим функцию на . В силу линейных свойств

. ↑

3) Пусть функция интегрируема на . Тогда на интегрируема функция и .4) Если на и .

5)Предположим, что непрерывна на .

2. Кольца, простейшие св-ва и примеры колец. Подкольца. Гоморфизм и изоморфизм колец.

Опр: Кольцом наз. непустое мн-во К, на котором определены бинарные операции + и ∙ эл-тов, удовлет. условиям:

1. Алгебра (К, +) – коммутат. группа с нейтр. эл-том 0;

2. Алгебра (К, ∙) – полугруппа, т.е. ∙ - ассоц.

3. Умн. дистрибутивно от-но слож., т.е. 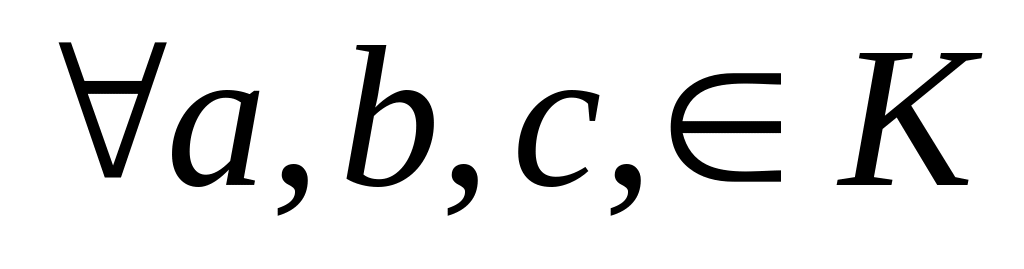a(b+c)=ab+ac; (b+c)a=ba+ca.

Примеры: (Z, +, ∙) – кольцо;Z[i]={a+bi | a, b Z}- кольцо цел. Гауссовых чисел (C, +, ∙); ({A=(α_ij)_n | α_ij F}, +, ∙) – кольцо.Кольцо К наз-ся коммутативным, если .Кольцо К наз-ся кольцом с единицей, если (К, ∙) – моноид, т.е. нейтральн. элемент относительно умножения, который называется единицей кольца.Кольцом целостности наз. ненулевое коммут. Кольцо с единицей без делителей нуля, т.е. вып. усл.:

1. Существует единица; 2) умн. коммутативно; 3) К – без делителей нуля, т.е. 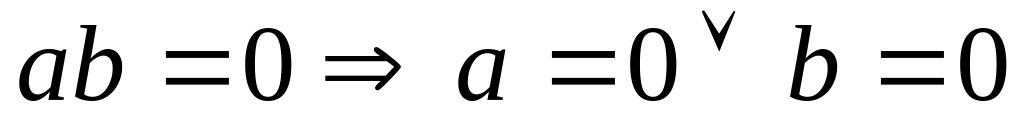. 4) 0≠1.

Опр: Подкольцом кольца К наз-ся непуст. подмн-во Н, удовл. услов:

1.(Н,+)-подгруппа аддит. гр. (К,+), т.е. a, b H a-b H;

2. подмн-во Н замкнуто от-но умн.: a, b H→ a∙b H.

Примеры: К=(Z, +, ∙) – кольцо. H={2z | z Z}Н-подкольцо. Н={nz | z Z} H- подкольцо.

Простейшие свойства колец.

3) –(-а)=а; 4) 0∙а=а∙0=0;

5) (-a)b=a(-b)=-(ab); 6) (-a)(-b)=ab; 7) (a-b)c=ac-bc и c(a-b)=ca-cb.

↓ 1) a+b=a; b=b+0=(-a+a)+b=-a+(a+b)=-a+a=0

2) a+b=0; b=0+b=(-a+a)+b= -a+(a+b)=-a+0=-a

3) В аддитивной группе кольца (-а)+(-(-а))=-а+а. Отсюда по закону сокращения -(-а)=а

4) В силу дистрибутивности умножения относит. «+»: 0∙а+а∙0=(0+0)а=0∙а, т.е. 0∙а+0∙а=0∙а по св-ву 1 0∙а=0

5) По св 4 и дистр. умнож. относит. «+»: ab+(-a)b=(a+(-a))b=0∙d=0, т.е. ab+(-a)b=0 по св 2 (-a)b=-(ab) (аналогично 2-е рав-во)

6) По св. 5 и 3 (-a)(-b)=-((-a)b)=-(-(ab))=ab

7) По св 5 и дистирибут. умнож. относит. «+» (a-b)c=(a+(-b))c=ac+(-b)c=ac+(-bc)=ac-bc (аналог 2-е)↑

Опр.: Отобр φ:(К₁, +,∙) → (К₂, )- гомоморфизм, если сохр. операции:

Опр.: Изоморфизмом колец наз-ся биективный гомоморфизм, т.е. отобр. φ:К₁ → К₂ наз. изоморфизмом, если: 1) φ – биекция, 2) φ – сохр. опер.

Билет №11