Билет №1.

1. Теорема Вейерштрасса о пределе монотонной последовательности.

Опр: Числовая функция f, заданная на множестве нат.чисел N(f:N→R) наз.числовой последовательностью.Если последовательность задана на всем множестве N чисел, то она называется бесконеч., а если на N от 1 до к, то конечной.Обоз.: 1). (х_n), где х_n=f(n) (n N); 2). x₁, x₂, x₃, …, x_n, ..x₁- первый член числ. послед-ти; x₂ – второй член числ. послед-ти; x_n – n-й или общий член послед-ти.Члены последовательности можно геометр. изображать с помощью точек: координатной прямой; координатной плоскости.Опр: Последовательность (х_n) назыв. возрастающей (в широком смысле), если . В частности, если всегда х_n+1> х_n последовательность назыв. возрастающей в узком или строгом смысле.Опр: Послед. (х_n) назыв. убывающей (в широком смысле), если В частности, если всегда х_n+1< х_n она называется убывающей в узком или строгом смысле.Опр: Возр. и убыв. послед-ти назыв. монотонными (в широком или узком смысле)Опр: Послед. (х_n) назыв. ограниченной сверху, если сущ-ет число М, называемое ее верхней гранью, такое, что .Опр: Послед. (х_n) назыв. ограниченной снизу, если сущ-ет число m, называемое ее нижней гранью, такое, что .(не превосходит)Опр: Послед-ть наз. ограниченной, если она ограничена сверху и снизу.Опр: Число а назыв пределом числовой послед. (х_n) при n → ∞, если

Теорема ВЕЙЕРШТРАССА.Люб.неубыв. и огран.сверху посл-ть имеет предел. Люб.невозр. и огран.снизу посл-ть имеет предел.

↓Пусть посл-ть - неубыв.: . В силу принципа верх.грани сущ. (всякое огран.сверху мн-во имеет точн.верх.грань, т.е. Необ.док-ть,что : : . В силу неубыв. посл. . Тогда в силу пред.нер-в имеем: .

↑

2. Понятие вектора. Линейные операции над векторами и их св-ва.

В школьном курсе геом. изуч-ся понятие направленного отрезка («НО»)

Рассмотрим произвольный отрезок. На нем можно указать два направления: от одного конца к другому и наоборот. Чтобы выбрать одно из направлений, один конец отрезка назовем началом, а другой – концом, и будем считать, что отрезок направлен от начала к концу.

Опр: Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется «НО».

В

А

. Точка А – начало; точка В – конец «НО»

Из определения «НО» следует, что любые 2 различные точки А, В определяют направленный отрезок АВ. Будем считать, что и совпадающие точки также определяют направление. «НО», у которого начальная и конечная точки совпадают называется нулевым «НО».

.

П

В

усть - «НО», - «НО» противоположный данному «НО»

А

= ; = ;

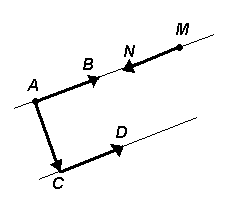
Два «НО» называются коллинеарными, если они лежат на одной прямой или

на парал-х прямых.

Нулевой «НО» коллинеарен любому «НО». Два ненулевых коллинеарных «НО» называются сонаправленными (противоположно направленные), если они имеют одинаковое

направление (протвоположн. направл.) .

Длиной или модулем «НО» называется длина обычного отрезка

АВ. . Длина нулевого «НО» считается = 0.

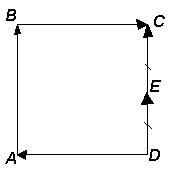
Опр: Два «НО» называются равными если: 1. Длины равны .

2. Коллинеарны .

Для «НО» : 1). ; 2). .

Эти «НО» противоположны друг другу

3. Сонаправленны .

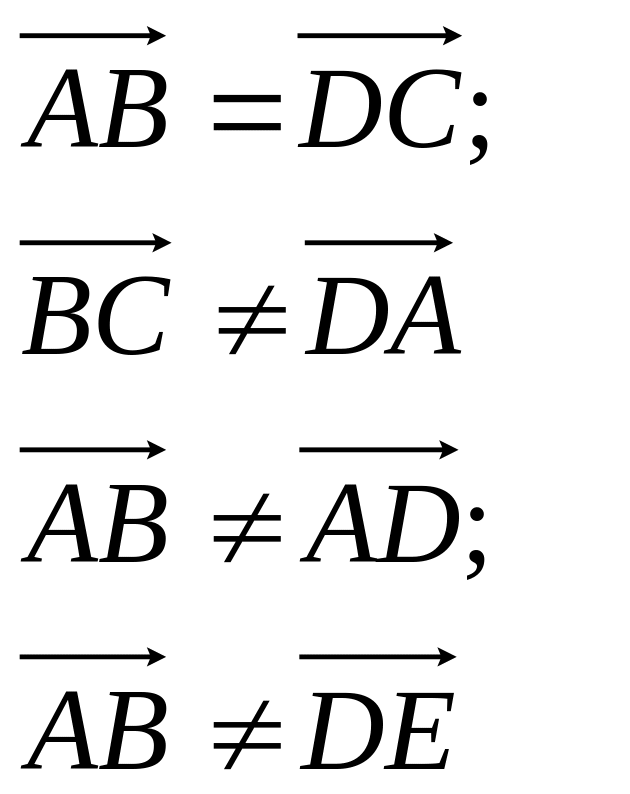
А

С

Лемма 1: Два «НО» равны один из них можно преобразовать

в другой с помощью //-го переноса, совмещающего их начальные точки.

Т

В

еорема 1: Отношение равенства «НО» обладает 3-мя свойствами:

1

D

). Оно рефлексивно, т.е. (каждый «НО»равен самому себе);

2 ). Симметрично, т.е. ; 3). Транзитивно, т.е. .

Следствие: Из Т1 следует, что отношение равенства равных отрезков является отношением эквивалентности.

Поэтому мно-ва всех «НО» разбивается отношением равенства на непересекающиеся классы.

В состав 1 класса входят все равные м/у собой «НО». «НО» из разных классов не раны м/у собой.

пр: Геометрическим вектором называется мно-во всех равных «НО». В этом случае отдельный «НО» из класса называется представитель-вектор.

Опр С: Каждый «НО» определяет некоторый геом.вектор, причем равные «НО» определяет один и тот же геометрический отрезок. А не равные «НО» определяют различные векторы.

Эти 3 «НО» определяет один «НО»

Откладывание вектора от точки.

Пусть определяет .

Вектор а отложим от точки А, т.к. из

определения С все равные «НО» определяет один и тот же вектор, то можно считать, что этот вектор отложен от любой точки пространства. При этом от заданной точки О вектор а можно отложить единственным способом, т.е. .

Сложение векторов и его сво-ва.

П

A

усть - два вектора. Отметим произвольную точку О и отложим от этой точки , равный . Затем от точки А , равный . называется суммой векторов . Это правило сложения векторов называется правилом

треугольника. Из правила треугольника вытекает правило 3-х точек

B

Это верно для точек А, В, С, которые лежат на одной прямой и даже если они совпадают

B

O

Свойства сложения векторов.

1 ⁰. Сложение векторов коммутативно:

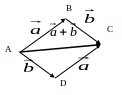
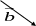
↓ Рассмотрим когда не коллинеарны. От произвольной точки А

отложим векторы и на этих векторах построим

параллелограмм ABCD, как показано на рис. По правилу треуг-ка

Рис.1

. Аналогично . ↑

2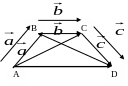 ⁰. Слож. вект. ассоциативно:

↓

От произвольной точки А отложим

от точки В – а от точки С - .

Применяя правило треугольника, получим:

Отсюда следует, что ↑

3⁰. Во мно-ве векторов

4⁰.

- взаимно противоположны.

При док-ве 1⁰ мы обосновали правило параллелограмма сложения неколлинеарных векторов: чтобы сложить , нужно отложить от какой-нибудь точки А и построить параллелограмм ABCD (рис. 1). Тогда .

Сво-ва сложения векторов полностью совпадают со сво-ми сложения рациональных чисел, поэтому можно использовать и те выводы, которые вытекают из свойств сложения рациональных чисел.

Сумма нескольких векторов.

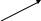
. Практически при сложении нескольких векторов применяется правило многоугольника.

A₁

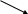
O

A₂

A₃

A₄

Умножение вектора на число.

Пусть дан не нулевой и действительной число λ. Произведение на λ называется такой вектор , что 1). . 2) . 3) а) λ>0, то ; б) λ<0, то .

Свойства. Теорема: справедливо: 1)

2)

↓ Пусть . По определению произведения на число . Отсюда следует, что . Докажем, что .

А) . Т.к. , а числа α и β одного знака, то одинаково направлены. Но векторы также одинаково направлены, следовательно .Б) . Аналогично убеждаемся, что .Учитывая равенства , приходим к выводу, что . ↑

3) ; 4) .

Приложение векторов к решению геометрических задач.

Примерная схема приложения векторов элементарной геометрии:

1. Перевести условие задачи на язык векторов. 2. Решить задачу в векторной форме. 3. Истолковать полученные результаты на языке геометрии.

Пример: Доказать теорему о средней линии треуг-ка.Средняя линия треугольника параллельна его основанию и равна его половине.

Дано:

Δ ABC,

M AB, AM=MB

N BC, BN=NC

Доказать:

1. MN//AC

2. MN=1/2AC.

Док-во:

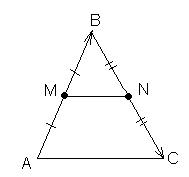
По правилу Δ: (1).

. Рав-во (1) перепишем с учетом (2):

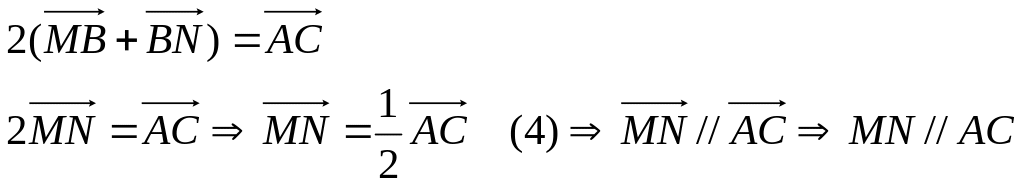
Посчитаем длину :

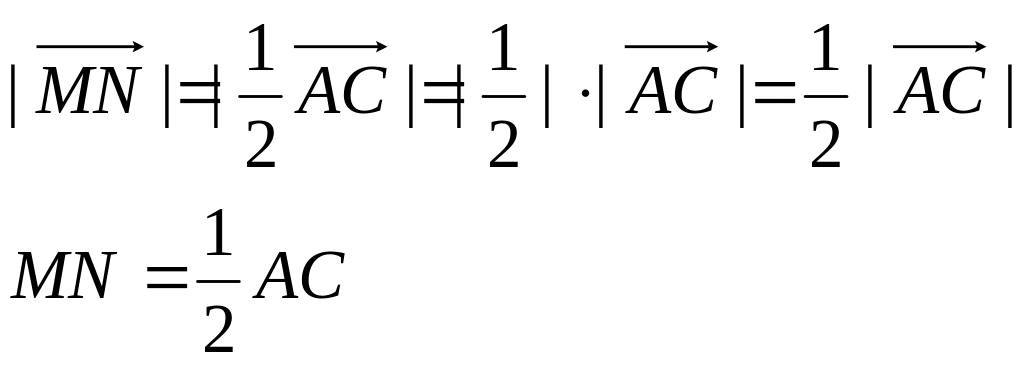
Разность векторов: Разностью любых векторов наз. такой вектор, который в сумме с вектором b дает вектор a.Т.(о сущ. и единст.разности векторов): для любых двух векторов сущ.вектор разности и притом единственный.

Дано: . Док-ть: (*). Док-во 1) дан , 2) ( ,3)

? Найдем ( + + ))+ . Док-во единственности: док.,что От противного: пусть . ))= . Т.о. Из т. следует, что векторы можно переносить из одной части в др.с противопол.знаком.

Билет №2.