29. Метод множників Лагранжа

Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення подальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.

Отже, для розв’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції.

Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:

(9.6)

за умов:

, (9.7)

де функції і мають бути диференційовними.

Задача (9.6)-(9.7) полягає в знаходженні екстремуму функції за умов виконання обмежень .

Переходимо до задачі пошуку безумовного екстремуму. Теоретично доведено, що постановки та розв’язання таких задач еквівалентні.

Замінюємо цільову функцію (9.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:

(9.8)

де – деякі невідомі величини, що називаються множниками Лагранжа.

Знайдемо частинні похідні і прирівняємо їх до нуля:

(9.9)

Друга група рівнянь системи (9.9) забезпечує виконання умов (9.7) початкової задачі нелінійного програмування.

Система (9.9), як правило, нелінійна.

Розв’язками її є і – стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (9.6)-(9.7) або можуть бути точками перегину (сідловими точками).

30. Економічна інтерпретація множників Лагранжа

Для з’ясування питання стосовно економічного змісту множників Лагранжа розглянемо застосування методу множників Лагранжа до задачі лінійного програмування як частинного випадку нелінійних задач. Нехай задача має вигляд:

(8.57)

(8.58)

Функція Лагранжа для даної задачі має вигляд:

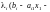
Якщо деякий змінний вектор є допустимим розв’язком задачі (8.57)—(8.58), то функція Лагранжа ідентич­на функції мети (8.57). Через те що виконуються умови , доданки виду у функції Лагранжа перетворюються в нуль і .

З необхідних умов існування екстремуму для функції Лагранжа можна помітити, що істотною для розгляду є лише умова рівності нулю частинних похідних по множниках Лагранжа. Отже, маємо задачу, що еквівалентна (8.57), (8.58):

max (8.59)

(8.60)

Розглянемо другу групу умов існування екстремальних точок функції Лагранжа, коли частинні похідні по дорівнюють нулю:

. (8.61)

Допустимо, що деякий вектор задовольняє умови (8.61), тоді для нього функція Лагранжа набуває вигляду:

.

Причому для того, щоб задовольнити умову (8.59), необхідно знайти такі значення вектора, що 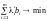, тобто приходимо до такої задачі:

, (8.62)

(8.63)

Очевидно, що пара задач (8.57), (8.58) та (8.62), (8.63) є парою спряжених задач (початковою та двоїстою), а множники Лагранжа — змінними двоїстої з цієї пари задач .

Отже, — це двоїсті оцінки ресурсів, «тіньові» ціни відповідних ресурсів виробництва.

Якщо поширити ці висновки на загальну задачу нелінійного програмування, додавши до задачі (8.57), (8.58) умову , то розв’язування можна здійснювати узагальненням методу Лагранжа .

В результаті отримаємо двоїсту задачу, що має вигляд:

,

,

.

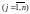Звідси отримуємо економічну інтерпретацію змінних параметрів початкової задачі, а також множників Лагранжа.

Очевидно, що залежно від економічної постановки задачі, функція Лагранжа та умови існування сідлової точки можуть мати різ­ну економічну інтерпретацію. Розглянемо задачу нелінійного програмування стосовно визначення оптимального плану виробництва продукції за умов використання обмежених ресурсів:

,

,

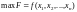Головна мета виробничої системи — максимізація прибутку від реалізованої продукції. Отже, цільова функція — це прибуток від реалізації продукції в обсягах , причому — нелінійна. Крім того, для виробництва продукції необхідне використання m видів сировини, обсяги кожного виду якої відомі і становлять . Система рівнянь може бути подана у вигляді: . Тобто, — обсяг і-го виду сировини, що використовується для виробництва продук­ції в обсязі Х, тоді — лишок і-го ресурсу після виробницт­ва продукції. Якщо , то це означає, що на виробництво продукції використано не весь запас ресурсу, а якщо — ресурс вичерпано і якщо , то це значить, що наявної (початкової) кількості сировини недостатньо для виробництва продукції на рівні Х.

Виробнича система здебільшого функціонує в конкурентному середовищі, що характеризується антагоністичними інтересами.

Як було показано вище, — це змінні двоїстої до поставленої певної задачі. Вони можуть являти собою ціну, за якою на конкурентному ринку продається чи купується одиниця і-го виду сировини. Якщо і , то така виробнича система може продати лишки сировини і отримати додатковий прибуток у розмірі . Якщо , то підприємство може закупити потрібну кількість сировини, витративши суму грошей, що дорівнює . Така закупівля дасть змогу забезпечити виробництво продукції на рівні Х. Отже, функція Лагранжа

являє собою загальний прибуток від виробництва, який включає прибуток від реалізації виготовленої продукції та прибуток від продажу лишків сировини (чи витрати на придбання потрібної кількості сировини) .

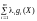За цін , що встановлюються на ринку, виробнича система прагне максимізувати прибуток шляхом визначення оптимального обсягу виробництва продукції . Отже, знаходиться значення функції Лагранжа при Х^*:

.

Оскільки прибуток формується на конкурентному ринку, слід розраховувати на встановлення цін на ресурси на мінімально мож­ливому рівні, тобто слід відшукати

.

Якщо для розглянутої задачі нелінійного програмування існує сідлова точка , то це означає, що існує такий рівень вироб­ництва та цін на ресурси , за яких має місце конкурентна рівновага:

=

Оскільки за теоремою Куна — Таккера для сідлової точки за будь-яких значень виконується нерівність:

,

то очевидно, що ніяка зміна рівня виробництва виробничою системою не збільшить прибутку і також ніяка зміна цін на ресурси в ринковому середовищі не зможе змен­шити прибутку . Отже, сідлова точка функції Лагранжа є точкою ринкової рівноваги.

Розглянемо інтерпретацію множників Лагранжа. Позначимо через вектор з компонентами, що означають обсяг і-го ресурсу у виробничій системі. Нехай 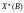означає, що оптимальний план задачі є функцією від значень наявних ресурсів В. Для спрощення допустимо, що функції та , мають властивості неперервності та диференційовності. І нарешті, допустимо також, що коли для і-го ресурсу , то за невеликих змін значення вектора В (що позначимо через ), які є досить близькими до В, також виконується нерівність .

За теоремою Куна — Таккера в задачах нелінійного програмування з обмеженнями — нерівностями для оптимального плану задачі має місце рівність ([3]):

.

Використовуючи правило диференціювання складної функції, можна написати таку рівність:

. Враховуючи, що , маємо:

.

Тепер допустимо, що деяке і-те обмеження активне в точці В, тобто . Тоді згідно з початковим допущенням це обмеження активне також і в деякому невеликому околі цієї точки. Враховуючи це, матимемо:

, де

Отже,

Тому є маргінальними змінами оптимального значення цільової функції за зміни . Аналогічно, як і в задачах лінійного програмування, можна вважати, що приблизно відповідає приросту цільової функції за збільшення обсягу відповідного і-го ресурсу на одиницю. Виходячи з цього, можна оцінити, як зміниться оптимальне значення цільової функції за змін обсягів ресурсів, не розв’язуючи нову задачу.