19. Знаходження потенціалів, критерій оптимальності.

Метод потенціалів - медод, який використовують для відшукання циклів з відємними вартостями.

Будемо вважати, що кожен із пунктів відправлення А_і вносить на перевезення одиниці вантажу (все одно куди) якусь суму , у свою чергу кожен із пунктів призначення також вносить за перевезення одиниці вантажу суму 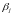. Ці суми передаються третій особі («перевізнику»). Позначимо

будемо називати псевдовартістю перевезення одиниці вантажу із пункту в пункт . Помітимо, що платежі , не обов’язково мають бути додатними: не виключено, що «перевізник» сам платить тому чи іншому пункту якусь премію за перевезення.

Позначимо всю сукупність платежів , через . Не уточнюючи, у який спосіб вони призначаються сформулюємо «теорему про платежі».

Теорема 1. Для заданої сукупності платежів сумарна псевдовартість перевезень

за будь-якого допустимого плану перевезень ( ) зберігає одне й те саме значення:

У цій формулі величина С залежить лише від сукупності платежів і не залежить від того, який допустимим планом ( ) використовується.

Теорема 2. Якщо в усіх базових клітинках ( )

а для всіх вільних клітинок ( )

то план перевезень оптимальний і ніяким способом не може бути здешевлений.

Не важко переконатися, що дана теорема справедлива також для виродженого плану, у якому деякі з базових змінних дорівнюють нулю. Дійсно, те, що в базових клітинках перевезення строго додатні, для доведення не суттєво: достатньо, щоб вони були невід’ємними.

Таким чином, доведено, що ознакою оптимальності плану ( ) є виконання умов:

для всіх базових клітинок; для всіх вільних клітинок.

План, для якого виконуються ці умови називається потенціальним, а відповідні платежі – потенціалами пунктів . Теорему 2 можна переформулювати так: будь-який потенціальний план оптимальний.

22, 23. Метод гілок та границь.

Часто в ЗЛП

за обмежень

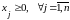
потрібно одержати розв’язок у якому деякі або всі компоненти мають бути цілими числами. Для цього використовують метод ланцюгів і границь. Схема розв’язання ЗЛП у цілих числах ЦЗЛП полягає в наступному:

1. Розв’язуємо ЗЛП (14.1), (14.2) за допомогою симплекс-методу (або будь-яким іншим методом) без умови цілочисельності змінних. Якщо змінні – цілі числа, то задачу можна вважати розв’язаною. Нехай змінна x_k набула не цілого значення x_k=α_k , α_k має дробову складову.

2. Розв’язуємо дві задачі:

1. (14.1), (14.2) за умови ;

2. (14.1), (14.2) за умови ,

де значок означає цілу частину числа, що в ньому міститься.

3. У випадку цілих розв’язків задач a) і b) порівнюємо одержані значення функцій L. Більше з них – оптимальне значенням , а змінні, за яких воно досягається, – розв’язок задачі.

4. Якщо ж знайдеться таке x_l, що не відповідає умові цілочисельності, тоді повторюємо виконання п.2, замінивши x_k на x_l. Таку процедуру повторюємо доти, доки всі потрібні змінні не стануть цілими.