1.Постановка задач математ.Програмування:

Схематично ек.систему можна подати у вигляді прямокутника:

y₁ y₂ … y_m

x

C_k

₁

x ₂ F

. .....

x _n

_{Параметр} C_k , k=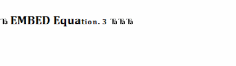 _{є кількісними характеристиками системи;}

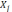, j=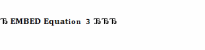 (керовані змінні, тобто можна змінювати в деякому інтервалі).

У_і , (некеровані змінні).

F – це обрана мета.

F= f(x₁,…,x_n; y₁,…,y_m; c₁,…,c_e) (1)

Задача мат.програмування формулюється так:

Знайти такі значення керованих змінних x_j, j=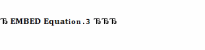 , щоб цільова функція набувала свого екстремал.значення.

F^*=min_xj(max) f( x₁,…,x_n; y₁,…,y_m; c₁,…,c_e) (2)

Можливості вибору x_j обмежені зовнішніми,щодо системи, умовами, параметрами виробничо-ек.системи. Ці процеси можна описати системою мат.рівностей та нерівностей виду:

q_r(x₁,…,x_n; y₁,…,y_m; c₁,…,c_e) 0 (3)

Для ек.системи параметри x_j мають бути невід’ємними:

x_j≥0, j=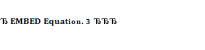 (4)

(2-4) – є ек.-мат.моделлю ек.системи

Розробляючи модель слід керуватися правилами:

1. Модель має адекватно описувати реальні технолог.та ек.процеси

2. В моделі слід враховувати все істотне в досліджув.явищі

3. Модель має бути зрозумілою для користувача

4. Потрібно забезпечити, щоб множинна змінних чи наборів була не порожньою

Будь-який набір змінних x₁,…,x_n , що задовольняє умови 3-4 назив.допустимим планом або план. Сукупність усіх розв’язків систем обмежень 3-4,тобто множина всіх допустимих планів становить обл.існування довільних планів. План, за якого цільова функція набуває екстрем.значення, наз.оптимальним. Оптим.план є розв’язком задачі (2-4).

4.Постановка злп

ЗЛП – означає знайти мін,мах функції при обмеженнях:

Z= c₁x₁+…+c_nx_n max (min) (1)

a₁₁x₁+a₁₂x₂+…+a_1nx_n b₁

_……… (2)

a_m1x₁+a_m2x₂+…+a_mnx_n b_m

x₁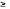 0, x_n 0 (3)

Отже, треба знайти значення змінних x₁ і x_n, які задовольнять умови (2-3), тоді як цільова функція набуває екстремального значення.

5.Зведення злп до канонічної форми:

Z= c₁x₁+…+c_nx_n max (min) (1)

a₁₁x₁+a₁₂x₂+…+a_1nx_n b₁

_……… (2)

a_m1x₁+a_m2x₂+…+a_mnx_n b_m

x₁ 0, x_n 0 (3)

Задачу 1-3 можна звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (2) всі b_і , (і=1, m) невід’ємні, а всі обмеження є рівностями. Якщо якесь b_і від’ємне, то помноживши і-те обмеження на «-1» дістанемо у правій частині відповідної рівності додатне значення. Коли і-те обмеження має вигляд нерівності:

а_і1x₁+a_і2x₂+…+a_іnx_n b_і ,

то останню можна звести , до рівності додати допоміжну змінну х_n+1

Аналогічно:

а_k1x₁+a_k2x₂+…+a_knx_n b_k ,

зводимо до рівності віднімаючи від лівої частини допом.змінну х_n+2

6. Властивості злп.

Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем.

Теорема 1.

Множина всіх планів задачі лінійного програмування опукла.

Теорема 2

Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин багатогранника розв’язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Теорема 3

Якщо відомо, що система векторів А1, А2….Аk (k≤n) у розкладі А1Х1+А2Х2…+.АnХn = A0 (X≥0) лінійно незалежна і така, що A1X1 + A2X2..+ AnXn =A0, де всі X_j≥0, то точка X = (x1,x2,...,xk,0,...,0) є кутовою точкою багатогранника розв’язків.

Теорема 4

Якщо X = (x1,x2,...,xk) - кутова точка багатогранника розв’язків, то вектори в розкладі А1Х1+А2Х2…+.АnХn = A0 (X≥0), що відповідають додатним Xj , є лінійно незалежними.