24. Основні теореми диференціального числення

Правило Лопіталя

Нехай функції f(x) і g(x):

1. диференційовані в деякому околі точки а і в цьому околі g'(x) ≠ 0;

2. одночасно є нескінченно малими або нескінченно ве­ликими в точці а;

3) існує границя відношення похідних цих функцій

Тоді існує границя відношення цих функцій причому

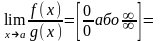
Приклад. За правилом Лопіталя знайти

Теорема Ферма. Якщо диференційована функція у = f(x) у деякій точці С інтервалу (а, b) набуває свого найбільшого або найменшого значення, то в цій точці похідна дорівнює нулю: f^’(С) = 0.

Теорема Ролля. Нехай задано функцію у = f (х), непере­рвну на відрізку [а, b] і диференційовану на інтервалі (а,b). Тоді, якщо f(a) - f(b), то всередині відрізка [а,b] знайдеться точка C (a<C<b), така що f^’(C)=0.

Теорема Лагранжа (про скінченні прирости функції). Нехай задано функцію y = f(x), неперервну на відрізку [а,b] і диференційовану на інтервалі (а,b). Тоді знайдеться точка , (а< <b), така що похідна функції в цій точці f^’'( ) дорівнюва­тиме відношенню

Теорема Коші (про кінцеві прирости двох функцій). Не­хай на відрізку [а,b] задано дві функції f(x) і φ(x). Якщо ці фун­кції неперервні на відрізку [а, b] і диференційовані на інтервалі (а,b), причому φ^’(x) ≠ 0, то на інтервалі (а,b) існує точка (а < < b), така що

25. Основні правила диференціювання функцій, заданих аналітично

Нехай С - стала і и та v - диференційовані функції. Тоді:

1. Похідна алгебраїчної суми двох диференційованих функцій дорівнює відповідній алгебраїчній сумі похідних цих функцій: .

2. Похідна добутку двох диференційованих функцій до­рівнює сумі добутків похідної першої функції на другу функцію і першої функції на похідну другої функції:

3. Сталий множник можна винести за знак похідної: ,

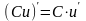де С - константа (число).

4. Похідна частки двох диференційованих функцій дорі­внює дробу, знаменником якого є квадрат знаменника цього дробу, а чисельником - різниця між добутком похідної чисель­ника на знаменник і добутком чисельника на похідну знаменни­ка:

5. Похідна складеної функції дорівнює добутку похідної функції у = f(u) за проміжним аргументом и на похідну проміж­ного аргументу за х. Якщо у = f(u(x)), то

27.Загальна схема дослідження функцій

Загальна схема дослідження функції y = f(x)

Перший етап (використання властивостей заданої функції)

1. Область визначення функції y = f(x)	D(f)
2. Парність, непарність і періодичність	f(x)- парна, якщо D(f) – симетрична відносно осі Оу; f(-x) = f(x); f(x)- непарна, якщо D(f) – симетрична відносно початку координат; f(-x) = - f(x); f(x)- періодична, якщо f(x+Т) = f(x)
3. Точки перетину графіка з осями координат	а) з віссю Ох: з рівняння f(x) = 0 знаходять х; б) з віссю Оу: x = 0, знаходять значення у = f(0)
4. Точки розриву. Асимптоти графіка функції у = f(х)	Вертикальні асимптоти – у точках нескінченного розриву 2-го роду функції у = f(х) Похилі асимптоти: y = kx + b,

Другий етап (використання похідної першого порядку)

5. Знайти похідну та критичні точки функції у = f(х)	f’(х) f’(х)=0 або f’(х) не існує
6. Проміжки зростання, спадання	f’(х)>0 – зростає, f’(х)<0 - спадає
7. Точки екстремуму функції у = f(х)	Якщо f’(х) змінює знак при переході через х0 з «+» на «-», то х0 = хmax, з «-» на «+», то х0 = хmin

Третій етап (використання похідної другого порядку)

8. Знайти другу похідну та критичні точки другого роду	f’’(х) f’’(х)=0 або f’’(х) не існує
9. Проміжки опуклості, угнутості	f’’(х)<0 – функція угнута; f’’(х)>0 – опукла
10. Точки перегину і значення функції в цих точках	Якщо f’’(х) змінює знак при переході через х0, то х0 – точка перегину

28. Поняття первісної та невизначений інтеграл

Означення: Функція F(x) називається первісною для ф-ії f(x) на проміжку І, якщо на цьому проміжку F`(x)=f(x) або dF(x)=f(x)dx.

Із означення виходить, що первісна F(x) – диференційована, а значить неперервна функція на проміжку І, і її вигляд суттєво залежить від проміжку, на якому вона розглядається.