Теорема про множину первісних

Якщо F(x) – первісна для функції f(х) на проміжку І, то:

1. F(x)+С – також первісна для f(x) на проміжку І;

2. будь-яка первісна Ф(х) для f(x) може біти представлена у вигляді Ф(х)= F(x)+С на проміжку І. (Тут С=const називається довільною сталою).

Невизначений інтеграл. Задача інтегрування

Означення: Операція знаходження первісних для ф-ії f(x) називається інтегруванням.

Задача інтегрування функції на проміжку полягає в тому, щоб знайти всі первісні функції на цьому проміжку. Для розв’язання задачі інтегрування функції достатньо знайти одну будь-яку первісну на розглядуваному проміжку, наприклад F(x), тоді (за теоремою про множину первісних) F(x)+С – загальний вигляд всієї множини первісних на цьому проміжку.

Означення: Ф-ія F(x)+С, зо являє собою загальний вигляд всієї множини первісних для ф-ії f(x) на проміжку І і позначається

де ­f(x) – підінтегральна ф-ія; f(x)dx – підінтегральний вираз; dx – диференціал змінної інтегрування.

Теорема Коші. Для існування невизначеного інтеграла для ф-ії f(x) на певному проміжку достатньо, щоб ­f(x) була неперервною на цьому проміжку.

Неінтегровні інтеграли – які неможливо записати через основні елементарні ф-ії.

29. . Властивості визначеного інтеграла

1) Якщо f(x)=c=const, то

2) Сталий множник можна виносити з-під знака визначеного інтеграла.

3) Якщо f₁(x) та f₂(x) інтегровні на [a;b], то:

4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл лише змінить свій знак на протилежний.

5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю.

6) Якщо f(x) – інтегровна в будь-якому із проміжків [a;b], [a;c], [c;b], то:

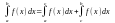
7) Якщо f(x)0 і інтегровна для x[a,b], b>a, то

8) Якщо f(x), g(x) – інтегровні та f(x)g(x) для x[a;b], b>a, то:

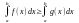
9) Якщо f(x) – інтегровна та mf(x)M, для x[a;b], b>a, то

10) (Теорема про середнє): Якщо ф-ія f(x) – неперервна для x[a;b], b>a, то знайдеться така точка x= c [a;b], що:

30.Визначений інтеграл

Поняття визначеного інтеграла

Означення: Якщо існує скінченна границя інтегральних сум S_n при _і­­0 і не залежить ні від способу розбиття [a;b] на частини х_і, ні від вибору точок _і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:

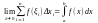
За означенням, визначений інтеграл – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.

Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.

31.Метод інтегрування частинами

Теорема: Якщо функції u(x) та v(x) мають неперервні похідні, то:

На практиці ф-ії u(x) та v(x) рекомендується вибирати за таким правилом: при інтегруванні частинами підінтегральний вираз f(x)dx розбивають на два множники типу udv, тобто f(x)dx=udv; при цьому ф-ія u(x) вибирається такою, щоб при диференціюванні вона спрощувалася, а за dv приймають залишок підінтегрального виразу, який мітить dx, інтеграл від якого відомий, або може бути просто знайдений.

Деякі типи інтегралів і їх заміни:

v(x):

де Р(х) – многочлен, Q(x) – алгебраїчна ф-ія.

32.Диференціальні рівняння

Нехай функція у = у(х) є кількісною характеристикою деякого явища (процесу). Часто, розглядаючи таке яви­ще, не можна безпосередньо виявити характер залежнос­ті у = у(х), а можна виявити залежність між величинами х та у і похідними функції у(х): у’,y”,…,y⁽ⁿ⁾. У результаті досліджуване явище (процес) описується співвідношен­ням, що зв'язує незалежну змінну х, невідому функцію у(х) та її похідні у’,y”,…,y⁽ⁿ⁾.

Означення. Співвідношення виду F(x, у’,y”,…,y⁽ⁿ⁾)= 0, що зв'язує незалежну змінну x, невідому функцію y(x) та її похідні у’,y”,…,y⁽ⁿ⁾, називається диференціальним рів­нянням.

Порядком диференціального рівняння назива­ється максимальний порядок похідної, що входить у це рівняння.

Розв'язком диференціального рівняння F(x, у’,y”,…,y⁽ⁿ⁾)= 0 назива­ється будь-яка п разів диференційована функція, яка при підстановці в це рівняння перетворює його на тотожність.

Приклад

На координатній площині Oxy знайти лінію, що про­ходить через точку O(0; 0), в якої кутовий коефіцієнт до­тичної, проведеної в будь-якій її точці, дорівнює подвоє­ній абсцисі цієї точки.

Нехай y = y(x) - рівняння шуканої лінії. Згідно з умовою ця лінія має в кожній своїй точці M(x; y(x)) дотич­ну, кутовий коефіцієнт якої, тобто y’, дорівнює 2x. Отже, маємо співвідношення y’ = 2x, що зв'язує незалежну змін­ну х і похідну y’ шуканої функції y. Це диференціальне рівняння першого порядку, з якого випливає, що функція у є первісною функції 2х. Отже, y = x² + c, де c - довільна стала.

З останньої формули випливає, що диференціальне рівняння y’ = 2x має безліч розв'язків.

Оскільки y = 0 при x = 0, підставивши ці значення у формулу у = x² + c, дістанемо c = 0. Таким чином, шука­ною лінією є парабола y = x².

Однією з основних задач теорії диференціальних рів­нянь є знаходження їхніх розв'язків. У найпростіших ви­падках ця задача зводиться до знаходження інтегралів, тому процес відшукання розв'язків диференціального рів­няння називається його інтегруванням.

33-34.Однорідні і лінійні диф.рівняння

Функція f(x,y), для якої викону­ється тотожність

f(tx,ty)= t^k f(x,y)

при всіх можливих t ≠ 0, де k — деяке число, називається однорідною функцією ступеня однорідності k.

Наприклад, — однорідна функція сту­пеня однорідності .

Диференціальне рівняння виду y’ = f(x,y) називається од­норідним відносно змінних х та у, якщо f(x,y) — однорід­на функція нульового ступеня однорідності (ступеня одно­рідності k = 0, тобто справджується тотожність

f(tx,ty)= t^k f(x,y)

при всіх можливих t ≠ 0.

Поклавши в тотожність дістанемо (у цьому ланцюзі рівностей остання є по­значенням), тобто однорідну функцію нульового ступеня однорідності можна зобразити як функцію відношення .

Тому однорідне диференціальне рівняння y’ = f(x,y) можна пе­реписати у вигляді .

Виконавши підстановку y = ux, де u — невідома функція x, що має похідну, рівняння запишемо у вигляді u’x + u = або .

Останнє рівняння є диференціальним рівнянням з ві­докремлюваними змінними. Інтегруючи його і підставля­ючи замість и відношення , прийдемо до загального роз­в'язку або до загального інтеграла диференціального рів­няння.

При фактичному інтегруванні однорід­ного диференціального рівняння досить переконатися в тому, що рівняння належить до типу, який розглядається, і безпосередньо застосувати підстановку y = ux.

Приклад

Проінтегрувати диференціальне рівняння .

Це диференціальне рівняння є однорідним віднос­но змінних х та у. Застосуємо підстановку y = ux. Маємо або .

Відокремивши змінні, дістанемо Проінтегрувавши останнє диференціальне рівняння, матимемо або . Вираз , набуває будь-якого значення з множини R. З урахуванням підстановки y = ux маємо , і, отже,

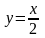При відокремленні змінних було втрачено розв'язок рівняння , тобто розв'язок вихідно­го рівняння. Цей розв'язок можна включити у формулу , знявши обмеження Отже, загальним розв'язком заданого диференціаль­ного рівняння є функція , де c — довільна стала.

Лінійні рівняння.

Диференціальне рівняння типу

називається лінійним диференціальним рівнянням першо­го порядку.

Будемо шукати розв'язок диференціального рівняння у вигляді добутку y = uv, де u i v — невідомі функції х, кожна з яких має похідну. Одну з цих функцій можна вибрати довільно, інша має бу­ти означена так, щоб функція була розв'язком рівняння.

Знайшовши y’ = u’v = uv’ і підставивши вирази y’ та y у диференціальне рівняння , дістанемо u’v + uv’+ p(x)uv = q(x).

Виберемо одну із функцій, наприклад и, так, щоб рів­няння мало простий вигляд. Для цього в диферен­ціальному рівнянні uv’ + v(u’+ p(x)u) = q(x) прирівняємо до нуля вираз у дужках: u’+ p(x)u = 0.

Це — диференціальне рівняння з відокремлюваними змінними.

Відокремивши змінні, дістанемо

Проінтегрувавши це диференціальне рівняння, знайдемо , де — деяка первісна функції p(x), a c₁ — довільна стала. Тому , звідки , й, отже,

При відокремленні змінних було втрачено розв'язок u = 0 диференціального рівняння. Цей розв'язок можна включити у формулу , знявши обмеження

Отже, загальний розв'язок диференціального рівнян­ня має вигляд , де c₂ — довільна стала.

Як функцію u візьмемо який-небудь час­тинний, відмінний від нульового (u = 0), розв'язок, нап­риклад

(випадок с₂ = 1). Підставивши цей вираз у диферен­ціальне рівняння, дістанемо , звідки й, отже,

де 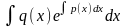— деяка первісна функції (вважаємо, що вона існує), а с — довільна стала.

Підставивши знайдені вирази функцій и та v у формулу y=uv, остаточно знайдемо

де під інтегралами розуміють деякі відповідні первісні, а с — довільна стала.

Можна показати, що дана формула дає загальний розв'язок диференціального рівняння.

Зазначимо, що при фактичному інтегруванні лінійно­го диференціального рівняння першого порядку не обов'язково користуватися данною формулою; його можна проінтегрувати, користуючись методом, який було засто­совано при виведенні формули.