20. Границя функції.Неперервність ф-ії

Число В називається границею функції f(х) в точці а (при х → а), якщо для будь-якого 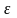> 0 знайдеться таке число 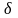>0, що п ри всіх х ≠ а, які задовольняють нерівність < виконуєть­ся нерівність 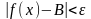, тобто .

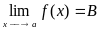Функція у = f(х) називається нескінченно малою в точці х₀, якщо .

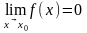Функція у = f(х) називається нескінченно великою в точці х₀, якщо .

Зауваження.

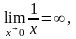
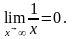
Односторонні границі

Якщо шукається 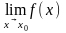при умові, що х приймає значення менші за х_о, то ця границя, якщо вона існує, називається лівосторонньою і позначається .

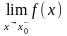Якщо х приймає значення більші за х₀, то границя назива­ється правосторонньою і позначається .

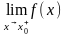Неперервність функції.

Функція у = f(х) називається неперервною в точці х₀, якщо границя функції в точці х₀ дорівнює значенню функції в цій точці:

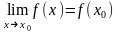
Функція у = f(х) називається неперервною в точці х₀, якщо f(х) визначена в точці х₀, границя зліва в точці х₀ дорівнює границі справа в цій точці і дорівнює значенню в ній функції:

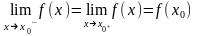
Функція у = f(х) неперервна на проміжку, якщо вона неперервна в кожній точці цього проміжку.

Функція у = f(х) неперервна на відрізку [а;b], якщо вона неперервна на проміжку (а; b) і неперервна в точці х = а справа і в точці х = b зліва.

Властивості неперервних функцій

Теорема 1. Нехай функції у = f(x) і у = g(х) - неперервні на інтервалі (а;b). Тоді їх наведені далі комбінації також непере­рвні

1) f(х)±g(х); 2) f(х)∙g(х);

3) f(х)/g(х); 4) u=g(x), y=f(u), то y=f(g(x)) неперервна в точці х₀.

Теорема 2 (Больцано-Коші). Нехай функція у = f(х) не­перервна на відрізку [а;b] і на кінцях відрізка набуває значень різних знаків. Тоді на проміжку (а;b) знайдеться точка с, в якій функція перетворюється на нуль: f(c)=0, а <с<b.

Теорема 3 (Вейєрштрасса). Неперервна на відрізку [а;b] функція у = f(х) досягає на цьому відрізку свого найбільшого і найменшого значень.

Теорема 4 (Коші). Нехай функція у = f(х) неперервна на відрізку [а;b] і на його кінцях набуває різних значень. Позначимо f(а) ≠ f (b). Тоді при будь-якому С: А<С<В знайдеться точка с є [а;b], така що f(c) = С.

21.Означення похідної

Нехай функція у = f(x) визначена на деякому проміжку X. Візьмемо довільну точку х₀ є X і надамо аргументу довільний приріст ∆х ≠ 0 такий, щоб точка х = х₀ + ∆х є X.

Функція набуде при цьому приросту ∆у = ∆f(х₀) = f(x) - f(x₀).

∆х = х - х₀ - приріст аргументу,

∆у = ∆f (х₀) = f(x₀ +∆х)- f(x₀) - приріст функції.

Похідною функції у = f(x) в точці х₀ називається границя відношення приросту функції до приросту аргументу, коли при­ріст аргументу прямує до нуля, тобто

,

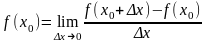де у'; f'(x); у'_х - позначення похідної, запропоноване Нью­тоном;

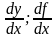- позначення Лейбніца похідної функції у = f(x).

Операція шукання похідної називається диференціюванням. Функція у = f(x) називається диференційованою в точці х₀, якщо існує похідна цієї функції в цій точці.

22.Зміст похідної

Дотичною до кривої в даній точці М називається гра­ничне положення січної MN, коли точка N наближається вздовж кривої до точки М.

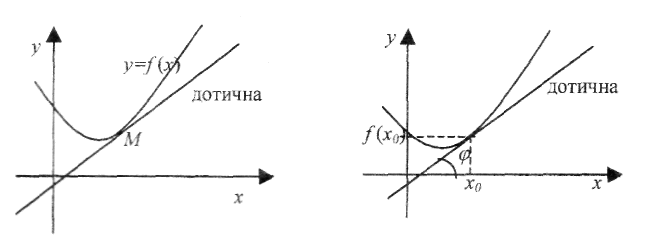
Значення похідної в точці х₀ дорівнює кутовому коефіці­єнту дотичної до графіка функції в точці х₀ і дорівнює тангенсу кута нахилу дотичної до додатного напряму осі ОХ:

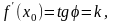
де k - кутовий коефіцієнт дотичної до графіка функції.

y = f(x₀) + f'(x₀)(x-x₀) - рівняння дотичної до графіка функції у = f(x) в точці з абсцисою х₀.

Фізичний зміст похідної

Якщо S = S(t) - залежність пройденого шляху від часу, то:

1. v = s'(t) - швидкість прямолінійного руху;

2. а = V’(t) - прискорення прямолінійного руху.

Похідні основних елементарних функцій

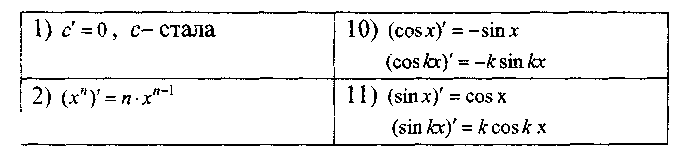
23.Диференціал ф-ії

Диференційованість функції

похідна диференціал функція змінна

Нехай функція   визначена в деякому околі точки . Виберемо прирости   і   так, щоб точка   належала розглядуваному околу і знайдемо повний приріст функції в точці :

.

Функція   називається диференційовною в точці М, якщо її повний приріст в цій точці можна подати у вигляді

,                     (1)

де   та   – дійсні числа, які не залежать від   та  ,   – нескінченно малі при   і   функції.

Відомо, що коли функція однієї змінної диференційовна в деякій точці, то вона в цій точці неперервна і має похідну. Перенесемо ці властивості на функції двох змінних.