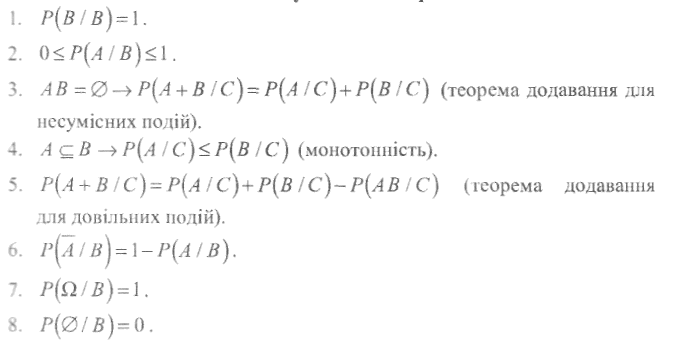- •1.Процент.Знаходження процентів від даного числа. Знаходження числа за його процентом
- •3.Види множин
- •4. Об'єднання множин,переріз множин,віднімання множин
- •[Ред.]Перетин множин
- •Доповнення та різниця множин
- •5. Поняття матриці. Види матриці
- •6.Транспонована матриця
- •7.Обернена матриця
- •8. Операції над матрицями.
- •10. Визначники 2-го та 3-го порядку. Властивості визначників.
- •11.Лінії в просторі. Види рівнянь площини.
- •12.Системи лінійних алгебраїчних рівнянь та методи їх розв′язування
- •2. Метод Крамера розв'язування систем лінійних рівнянь
- •3. Матричний метод розв'язування систем лінійних рівнянь
- •4. Метод Гаусса розв'язування систем лінійних рівнянь
- •Алгоритм методу Гаусса
- •13. Метод Гаусса розв'язування систем лінійних рівнянь
- •Алгоритм методу Гаусса
- •15. Дії з векторами, заданими в координатній формі
- •17.Елементарні функції.Окремі класи ф-їй
- •1 8.Способи задання ф-їй
- •19.Зростання та спадання ф-ії.Достатня умова
- •20. Границя функції.Неперервність ф-ії
- •21.Означення похідної
- •24. Основні теореми диференціального числення
- •27.Загальна схема дослідження функцій
- •Теорема про множину первісних
- •35.Диф.Рівняння 1-го порядку з відокремленими змінними.
- •Диференціальні рівняння і порядку
- •Диференціальні рівняння з відокремленими змінними.
- •Графічний метод розв’язування злп. Симплекс-метод.
- •40.Основні теореми теорії ймовірності.
- •Теореми множення та додавання випадкових подій.
- •41.Основні поняття математичної статистики
Графічний метод розв’язування злп. Симплекс-метод.
Симплекс-метод розв'язування задач лінійного програмування
Одним з ефективних методів розв'язування задач лінійного програмування є симплекс-метод, який добре піддається програмуванню на ЕОМ, уможливлює довільну розмірність задач, тобто не залежить ні від кількості невідомих, ні від числа і вигляду обмежень.
Перш ніж розглянути положення методу, введемо необхідні визначення.
Оскільки задачі ЛП дають розв'язок економічній задачі, то замість слова "розв'язок" будемо говорити "план".
Розв'язок системи обмежень, у якому вільні невідомі дорівнюють нулю, називають базисним планом.
Будь-який невід'ємний розв'язок системи обмежень задачі ЛП називатимемо допустимим планом.
Допустимий базисний план називається опорним. Для того, щоб базисний план системи обмежень був опорним, необхідно і достатньо, щоб усі вільні члени були невід'ємні.
Допустимий план системи обмежень, що надає функції найбільшого (найменшого) значення, називатимемо оптимальним.
Таким чином, суть задачі ЛП полягає у тому, що серед усіх допустимих планів потрібно вибрати оптимальний. Оптимальний план шукають за допомогою симплекс-таблщь, які заповнюють за певними правилами, в основу яких покладено метод Йордана Гаусса.
Нехай потрібно розв'язати задачу L = c0+c1x1+c2x2+…+cnxn → extr
за
обмежень: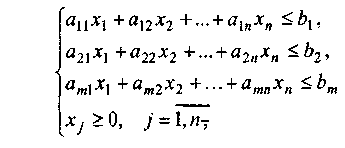
Алгоритм симплекс-методу
I. Записати задачу лінійного програмування в стандартній формі так, щоб:
1. Цільова функція Z максимізувалась.
Усі знаки були " ≤ ".
Праві частини bi були невід'ємними числами.
Привести систему до канонічного вигляду, для чого слід увести додаткові змінні t1≥ 0, t2 ≥ 0, …, tm ≥ 0.
Записати цільову функцію Z у такому вигляді: Z - c1x1 - c2x2 -…- cnxn = 0 (c0)
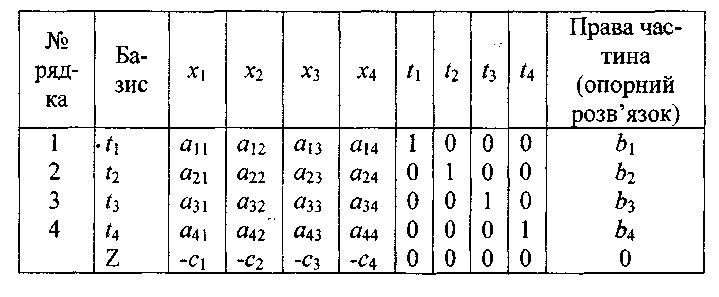
Записати задачу у вигляді розширеної симплекс-таблиці, яка містить також нову базисну зміну Z (приклад записаний для системи 4 рівнянь з 4 основними невідомими):
або у вигляді спрощеної симплекс-таблиці:
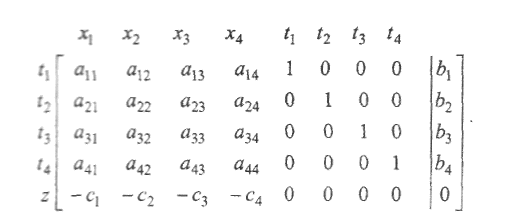
V. Визначити базисні змінні.
Як видно з таблиці, базисними змінними є t1, t2, t3, t4. Їм відповідає допустимий базисний розв'язок
t1 = b1, t2 = b2, t3 = b3, t4 = b4, х1 = 0, х2 = 0, х3 = 0, х4 = 0.
Алгоритм симплекс-методу полягає в переході від базису (t1, t2, t3, t4) до послідовності нових базисів шляхом заміни базисних змінних.
VI. Виконуємо послідовність симплекс-перетворень симплекс-таблиці, які приводять до максимізації цільової функції.
Симплекс-перетворення визначаються такими правилами:
Правило 1. Базисна змінна Z не підлягає заміні.
Означення. Коефіцієнти останнього рядка симплекс-таблиці, що відповідають небазисним змінним, називають індексами.
Критерій оптимальності розв'язку. Якщо всі індекси додатні, то цільова функція досягає максимального значення на даному базисі.
Правило 2. Симплекс-перетворення.
Якщо всі індекси додатні, то цільова функція має максимальне значення.
Нехай є від'ємні індекси.
Вибираємо найменший від'ємний індекс (тобто індекс, що має найбільше за абсолютною величиною значення). Цей індекс визначає вхідну змінну (ведучий стовпчик). Біля нього ставимо ↓.
Нехай у стовпчику вхідної змінної є додатні коефіцієнти (тільки додатні). Коефіцієнт, що стоїть у стовпчику вільних змінних (опорний розв'язок) навпроти додатного коефіцієнта, ділимо на цей коефіцієнт. Найменше із цих часток визначає вхідну змінну і ведучий елемент (він виділяється квадратиком).
Проводимо стандартну процедуру заміни базису на новий з урахуванням знайденого ведучого елемента (виводимо з базису стару базисну змінну та вводимо нову).
Ведучий елемент заміняємо одиничним. Для цього всі елементи, що стоять у ведучому рядку, ділимо на ведучий елемент.
5. Всі елементи, що стоять у ведучому стовпчику, крім ведучого, заміняємо на 0.
6. Дивимось на нові індекси.
Правило 3. Застосовуємо правило 2 скінчене число раз до того часу, поки всі індекси не стануть додатними.
Зауваження 1. Якщо у симплекс-таблиці є від'ємний індекс, а у відповідному йому стовпчику всі коефіцієнти недодатні, то задача не має оптимального розв'язку.
Зауваження 2. Якщо всі індекси в симплекс-таблиці невід'ємні, але в останньому рядку є нульові індекси, то досягнуте оптимальне значення не єдине.
Приклад. Розв'язати ЗЛП симплекс-методом:
z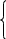 = 3x1
+ 2x2
→ max
при обмеженнях
= 3x1
+ 2x2
→ max
при обмеженнях 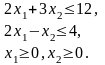
Розв'язання
З
ведемо
ЗЛП до канонічного вигляду 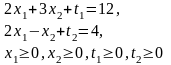
Запишемо цільову функцію у вигляді z - 3x1 - 2x2 = 0.
Складемо симплекс-таблицю

План оптимальний х1= 3, х2= 2, z = l3.
Перевірка: z = 3*3 + 2*2 = 13.
Відповідь. хопт= (3;2), zmax=13.
Графічний метод розв'язування задач лінійного програмування
Використовують графічний метод розв'язування задач лінійного програмування для задач з двома змінними.
Загальна математична постановка задачі лінійного програмування для двох змінних: знайти значення змінних х, у, які доставляють екстремум заданої лінійної цільової функції z = c1x1 + c2x2
за
лінійних умов-обмежень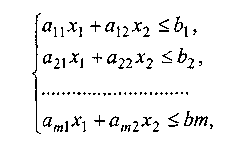
Алгоритм графічного методу розв'язання задач лінійного програмування
1. Будуємо багатокутник розв'язків:
а)
будуємо
граничні прямі: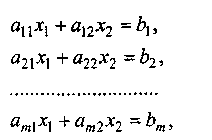
б) для кожної граничної прямої визначаємо півплощину розв'язків. Для цього підставляємо у відповідну нерівність координати будь-якої точки (зручно брати точку (0, 0)). Якщо координати цієї точки задовольняють задану нерівність, то півплощина, яка містить цю точку, є розв'язком даної нерівності.
в) шуканий багатокутник розв'язків складатиметься з перетину цих півплощин розв'язків. Багатокутник розв'язків завжди міститься у першому квадранті.
2. Знаходимо оптимальну точку.
Теорема. Оптимальне значення задачі лінійного програмування досягається у вершині багатокутника розв'язків.
а) Будуємо вектор нормалі N (с1, с2) (вектор напрямків) прямої, який вказує напрямок зростання функції. Початок цього вектора знаходиться в точці (0,0), а кінець в точці (с1, c2), де числа с1, с2 - коефіцієнти цільової функції Z.
б) Надавши цільовій функції довільного дійсного значення, побудуємо лінію рівня, яка є перпендикулярною до вектора нормалі. Всі лінії рівня паралельні між собою.
в) Для знаходження точки максимуму функції пересуваємо лінію рівня в напрямку, який вказує вектор нормалі. Знайдемо вершину, де Z (х) набуває найбільшого значення.
г) Для відшукання точки мінімуму треба лінії рівня з’ясувати у напрямку, протилежному до вектора нормалі N.
3. Обчислюємо оптимальні значення:
а) знаходимо координати вершин max і тіп як спільний розв'язок рівнянь відповідних граничних прямих, що перетинаються в оптимальних вершинах;
б) знайдені координати підставляємо у формулу цільової функції і обчислюємо Zmax чи Zmin.
Часто на практиці зустрічаємо задачі, коли система обмежень зображується необмеженим многокутником розв'язків. У таких випадках одного або двох оптимальних значень може не існувати.
37-38. Транспортні задачі. Методи розв’язування.
Як організувати перевезення вантажів з одних пунктів в інші, щоб загальна вартість перевезень була мінімальною.
Економічна та математична постановка транспортної задачі
Нехай а1, а2, ..., ап - кількість товару, зосередженого в пунктах виробництва;
b1, b2, ..., bт - кількість товару, який необхідно завести в пункти споживання,
Xij - кількість товару, перевезеного з пункту Аi в пункт Bj
Cij - вартість перевезення одиниці продукції з Аi в пункт Bj
Запишемо задачу у вигляді таблиці.
-
Пункт виробництва
Пункт споживання
Запас
B1
B2
…
Bn
A1
X11
C11
X12
C12
…
X1n
C1n
a1
A2
X21
C21
X22
C22
…
X2n
C2n
a2
…
…
…
…
…
…
Am
Xm1
Cm1
Xm2
Cm2
…
Xmn
Cmn
am
Потреби
b1
b2
…
bn
Поставимо задачу так, щоб увесь товар з пунктів виробництва був вивезений; потреби кожного пункту споживання були задоволені; загальна вартість усіх перевезень з пунктів виробництва у пункти споживання була мінімальною.
Математична постановка транспортних задач.
Серед невід'ємних розв'язків системи рівнянь
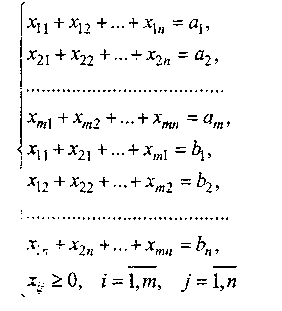
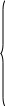
знайти
такий,
при якому цільова функція
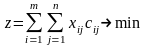 набуде
найменшого значення.
набуде
найменшого значення.
Умови існування розв'язків транспортних задач
Теорема
1. Для
того щоб транспортна задача мала
розв'язок необхідно і достатньо, щоб
запаси вантажу в усіх пунктах відправлення
дорівнювали загальній сумі потреб усіх
пунктів
призначення, тобто
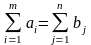
Таку транспортну задачу називають транспортною задачею з правильним балансом (або закритою), а якщо рівність порушується, то таку задачу називають транспортною задачею з неправильним балансом (відкритою).
Зауваження
1.
У разі перевищення запасів над потребами
вводиться
фіктивний (п+1)-й
пункт призначення з потребою
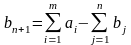 ,
а
відповідні вартості перевезень вважаються
рівними
нулю.
,
а
відповідні вартості перевезень вважаються
рівними
нулю.
Зауваження
2. У
разі перевищення потреб над запасами
вводиться
фіктивний (т+1)-й
пункт відправлення запасом вантажу
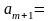
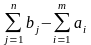 ,
а
відповідні вартості перевезень
вважаються
рівними нулю.
,
а
відповідні вартості перевезень
вважаються
рівними нулю.
Наслідок з теореми 1. Опорний план транспортної задачі може мати не більше т+п-1 відмінних від нуля невідомих, де т - число пунктів відправлення, an- споживання.
Методи розв'язування транспортних задач
1. Діагональний метод
Заповнюють клітинки матриці перевезень AіBj меншим з чисел її рядка і стовпчика, тобто числом тіп (аі, bj).
Згідно з цим методом послідовно заповнюють клітинки, починаючи з лівої кутової послідовно вичерпуючи запаси. Доцільно використовувати при розв'язуванні задач з допомогою електронно-обчислювальних машин.
2. Метод найменшої вартості
Відрізняється від діагонального послідовністю заповнення клітинок. Починають заповнювати ті клітинки таблиці, де вартості перевезень на даному етапі є мінімальними. Це забезпечує перевагу даного методу: отримання початкового опорного плану, який є більш близьким до оптимального.
39.Теорії ймовірностей.Випадкові події та їх ймовірності.
Випадкові події. Класифікація подій. Означення ймовірності.
Теорія
ймовірностей вивчає
математичні моделі масових однорідних
випадкових явищ (експериментів), які
мають властивість стійкості частот.
Експеримент визначається певною
сукупністю умов і його можливими
результатами.
Наслідки експерименту (або випробування)
називаються випадковими
подіями, тобто випадкова
подія -
це подія , яка може відбутись або ні,
внаслідок
проведення деякого експерименту,
результат якого наперед точно передбачити
не можна. Подія називається елементарною,
якщо
її не можна розкласти
на більш прості події. В протилежному
випадку подія називається складеною.
Наприклад,
якщо експеримент - підкидання грального
кубика, то події
 і
-
"випало і
очок"
і
-
"випало і
очок"
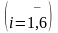 є елементарними. Вони вичерпують всі
можливі результати цього
експерименту. Очевидно, що подія А
- «випало
парне число очок» є складеною,
вона відбувається, коли відбувається
одна з елементарних подій
2
,
4,
6.
є елементарними. Вони вичерпують всі
можливі результати цього
експерименту. Очевидно, що подія А
- «випало
парне число очок» є складеною,
вона відбувається, коли відбувається
одна з елементарних подій
2
,
4,
6.
Означення 1. Простором елементарних подій, який описує дане випробування, називають довільну множину, між елементами якої і всіма можливими результатами цього випробування можна встановити взаємно однозначну відповідність.
Простір
елементарних подій будемо позначати
буквою
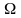 ,
елементарні події малими
буквами
(можливо
з індексами) і називати точками простору.
Ми будемо
розглядати тільки скінченні простори:
=
{
1,
2
,
...,
п},
N(
)
= п.
,
елементарні події малими
буквами
(можливо
з індексами) і називати точками простору.
Ми будемо
розглядати тільки скінченні простори:
=
{
1,
2
,
...,
п},
N(
)
= п.
Означення 2. Випадковими подіями називатимемо будь-які підмножини простору елементарних подій і позначатимемо їх буквами А, В, С...
При цьому простір називають достовірною або вірогідною подією, а порожню множину - неможливою подією.
Між випадковими подіями встановлюються певні відношення.
Означення 3. Кажуть, що подія А викликає подію В, або А є окремим випадком В, або В є наслідком А, якщо з відбуванням події А обов'язково відбувається подія В.
Позначають це відношення символом " " (включення) і пишуть А В . Дане відношення має очевидні властивості:
а) А А (рефлексивність),
б) А
В
В
С А
С
(транзитивність).
А
С
(транзитивність).
Означення 4. Події А і В називаються рівними, якщо А викликає В і В викликає А.
Позначають відношення рівності символом "=" і пишуть А = В . Відповідно до означення
А
= В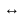 А
В
В
А
А
В
В
А
Відношення рівності є відношенням еквівалентності, тобто має властивості:
а) А = А (рефлексивність),
б) А = В В = А (симетричність),
в) А = В В = С А = С (транзитивність).
Операції над подіями та їх властивості (алгебра випадкових подій)
Над випадковими подіями (як над множинами) можна виконувати певні операції.
Означення 5. Сумою (або об'єднанням) двох подій А і В називається подія С, яка відбувається, коли відбувається принаймні одна з цих подій.
Позначають: С = А + В = A B .
Означення 6. Добутком (або перерізом) двох подій А і В називають подію Д яка відбувається, коли одночасно відбуваються обидві події.
Позначають: Д = АВ =А В.
Події А і В називаються несумісними, якщо їх добуток - неможлива подія, тобто АВ = Ø.
Означення 7. Різницею двох подій А і В називають подію Е, яка відбувається, коли відбувається А і не відбувається В.
Позначають: Е =А — В =А\В .
Означення
8. Протилежною
до події А
називають подію
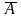 =
Ω - А
.
=
Ω - А
.
Означення 9. Симетричною різницею двох подій А і В називають подію F, яка відбувається, коли відбувається А і не відбувається В або відбувається В і не відбувається А.
Позначають симетричну різницю символом ∆. Відповідно до означення :
А∆В= (А-В)+(В-А).
Множина випадкових подій відносно означених операцій утворює булеву алгебру, тобто виконуються такі рівності:
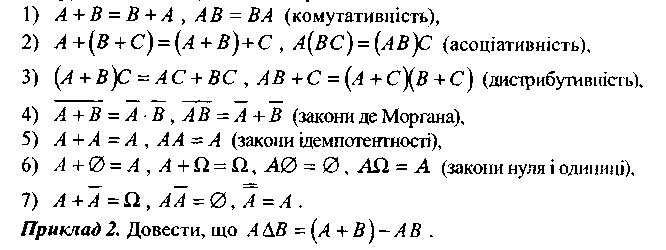
Класичне означення ймовірності
Нехай
простір елементарних подій
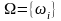 скінченна множина (N(Ω)
= п)
і
всі елементарні події
скінченна множина (N(Ω)
= п)
і
всі елементарні події
 рівноможливі.
рівноможливі.
Рівноможливість означає, що ні одна з них не має переваг перед іншою, тобто всі мають однакові шанси на реалізацію при даному експерименті. Нехай А = {ωіk} - деяка випадкова подія і N(A)=m. Число n називають числом всіх можливих наслідків випробування, а число т - числом наслідків випробування, які сприяють події А. Можливість появи події А при заданому випробуванні може бути охарактеризована за допомогою числа, що називається ймовірністю події.
Означення 10. Ймовірністю події А називають відношення числа наслідків випробування, що сприяють появі події А, до числа всіх можливих наслідків цього ж випробування.
Позначають ймовірність події А символом Р(А). Відповідно до означення
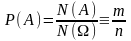
Властивості ймовірності:
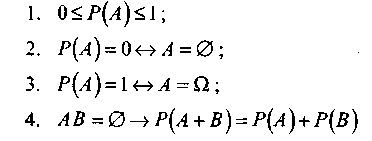 (теорема
додавання для несумісних подій);
(теорема
додавання для несумісних подій);
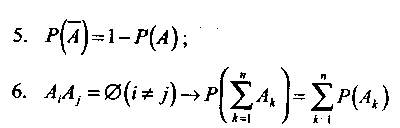 (теорема
додавання для попарно несумісних
подій);
(теорема
додавання для попарно несумісних
подій);
A
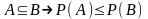 (монотонність
ймовірності);
(монотонність
ймовірності);
Р(А + В) = Р(А) + Р(В) — Р(АВ) (теорема додавання для довільних подій);
![]()
Для знаходження ймовірності події можна запропонувати такий алгоритм:
Будуємо простір елементарних подій Ω та обчислюємо N(Ω).
Описуємо подію А і обчислюємо N(A).
Знаходимо шукану ймовірність за формулою .
Зауваження. Класичним означенням ймовірності можна користуватись, якщо множина можливих наслідків стохастичного експерименту скінченна і ці наслідки рівноможливі. У випадку порушення хоч однієї з цих вимог, означення незастосовне. В зв'язку з цим, поряд з класичним використовується статистичне (частотне) означення ймовірності, згідно з яким за ймовірність події А наближено приймають її відносну частоту.
Умовна ймовірність та її властивості
Якщо
ймовірність події А
обчислюється
при умові, що відбувалась подія
В,
то
така ймовірність називається умовною
ймовірністю і
позначається символом
Р(А/В).
Ймовірність
Р(А)
називається
безумовною.
Розглянемо
випадок класичного означення ймовірності.
Нехай Ω
- простір
елементарних подій, А,
В -
деякі випадкові події. При знаходженні
Р(А/
В)
можливими
наслідками випробування потрібно
вважати ті, при яких настає подія В,
а
сприятливими
- ті, при яких відбуваються обидві події
А
і
В,
тобто
подія АВ.
От
же,
згідно з класичним означенням ймовірності
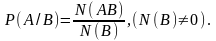
Поділивши
чисельник і знаменник у правій частині
формули на N(Ω),
будемо
мати,
що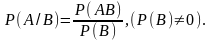
Примітка. Якщо Р(В) = 0, то умовна ймовірність Р(А/В) не визначена. Як правило, в цьому випадку її вважають рівною нулю.
Властивості умовної ймовірності: