- •Электричество и магнетизм практикум по физике
- •Устройство и принцип действия электроизмерительных приборов
- •1. Основные электроизмерительные приборы
- •2. Классификация приборов по принципу действия
- •3. Чувствительность и цена деления электроизмерительного прибора
- •4. Расширение пределов измерений приборов
- •Элементы теории погрешностей при электрических измерениях
- •1. Погрешности приборов
- •2. Оценка погрешностей электрических измерений
- •3. Определение ошибок косвенного измерения физической величины
- •4. Определение наиболее выгодных условий измерения
- •5. Проведение физических измерений и оформление полученных результатов
- •6. Запись экспериментальных результатов
- •Лабораторная работа № 1 измерение сопротивлений мостиком уитстона
- •1. Метод вольтметра и амперметра.
- •2. Метод омметра.
- •3. Мостовой метод или метод мостика постоянного тока (мостик Уитстона).
- •Устройство и принцип действия мостика Уитстона
- •Проведение измерений
- •Обработка результатов
- •Погрешность измерений
- •Техника безопасности
- •Содержание отчета
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Описание экспериментальной установки и проведение измерений
- •Обработка результатов
- •Техника безопасности
- •Содержание отчёта
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 3 определение эдс методом компенсации
- •Теория метода
- •Метод компенсации и описание установки
- •Проведение измерений и обработка результатов
- •Техника безопасности
- •Содержание отчета
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 4 изучение электростатического поля
- •Теория метода
- •Методика исследования
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Техника безопасности.
- •Содержание отчета
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Лабораторная работа 5 измерение электрической емкости мостиком сотти
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Техника безопасности
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 6 изучение гальванометра
- •Проведение измерений и обработка результатов
- •Техника безопасности
- •Погрешность измерений
- •Содержание отчета
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Техника безопасности
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 8 изучение законов кирхгофа
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений
- •1. Определение эдс источников тока участков цепи
- •2. Проверка первого закона Кирхгофа
- •3. Проверка второго закона Кирхгофа
- •Погрешность измерений
- •Содержание отчета
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 9 исследование зависимости электрического сопротивления металла от температуры
- •Теория метода
- •Описание установки
- •Проведение измерений
- •Обработка результатов
- •Техника безопасности
- •Содержание отчета
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •1. Измерение электрической постоянной.
- •2. Измерение относительной диэлектрической проницаемости диэлектриков.
- •Погрешность измерений
- •Техника безопасности
- •Содержание отчета
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 11 определение напряженности земного магнитного поля с помощью тангенсгальванометра
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений
- •Обработка результатов и погрешность измерений
- •Содержание отчета
- •Техника безопасности
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 12 исследование индуктивности соленоида
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений
- •Обработка результатов
- •Содержание отчета
- •Техника безопасности
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 13 изучение эффекта холла
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Содержание отчета
- •Техника безопасности
- •Вопросы допускного контроля
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Содержание отчета
- •Техника безопасности
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 15 изучение электромагнитной индукции
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений
- •Обработка результатов
- •Техника безопасности
- •Содержание отчета
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 16 исследование резонанса в колебательном контуре
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений
- •Обработка результатов измерений
- •Техника безопасности
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 17 определение длины электромагнитной волны с помощью измерительной линии лехера
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений
- •Техника безопасности
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Содержание отчета
- •Техника безопасности
- •Вопросы для допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 19 исследование энергетического режима цепи синусоидального тока
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Техника безопасности
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Лабораторная работа № 20 определение точки кюри ферромагнетика
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов
- •Содержание отчета
- •Техника безопасности
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Исследование намагничивания ферромагнетика
- •Теория метода
- •Описание экспериментальной установки
- •Проведение измерений и обработка результатов Первый вариант
- •Второй вариант
- •Содержание отчета
- •Техника безопасности
- •Вопросы допускного контроля
- •Контрольные вопросы
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
Лабораторная работа № 16 исследование резонанса в колебательном контуре
Цель работы: получение резонансных кривых для контура, определение параметров контура — емкости конденсатора и индуктивности катушки.
Теория метода
Р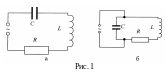 ассмотрим
теорию вынужденных электромагнитных
колебаний в колебательном контуре,
включающем последовательно соединенные
конденсатор, катушку индуктивности
и резистор. В контур, содержащий емкость
C,
индуктивность L
и
активное сопротивление R,
включена
внешняя переменная ЭДС
ассмотрим
теорию вынужденных электромагнитных
колебаний в колебательном контуре,
включающем последовательно соединенные
конденсатор, катушку индуктивности
и резистор. В контур, содержащий емкость
C,
индуктивность L
и
активное сопротивление R,
включена
внешняя переменная ЭДС
![]() имеющая циклическую частоту ω
(рис. 1а). В любой момент времени в
колебательном контуре выполняется
второй закон Кирхгофа: сумма падений
напряжений на участках контура равняется
сумме действующих в нем ЭДС.
имеющая циклическую частоту ω
(рис. 1а). В любой момент времени в
колебательном контуре выполняется
второй закон Кирхгофа: сумма падений
напряжений на участках контура равняется
сумме действующих в нем ЭДС.
В
рассматриваемом случае падение напряжения
происходит на активном сопротивлении
![]() и на конденсаторе
и на конденсаторе
![]() .
В
контуре имеются две ЭДС: самоиндукции
.
В
контуре имеются две ЭДС: самоиндукции
![]() и внешняя
.
На
основании второго закона Кирхгофа
запишем:
и внешняя
.
На
основании второго закона Кирхгофа
запишем:
![]() .
.
Дифференцируя
это выражение по времени и учитывая,
что
![]() ,
получаем
дифференциальное уравнение вынужденных
колебаний тока в контуре с последовательно
соединенными С,
L,
R:
,
получаем
дифференциальное уравнение вынужденных
колебаний тока в контуре с последовательно
соединенными С,
L,
R:
![]() .
.
Из
эксперимента известно, что колебания
тока имеют ту же частоту, что и внешняя
ЭДС, но сдвинуты относительно ее по
фазе на φ:
![]() .
Подставляя
это возможное решение в дифференциальное
уравнение, после математических
преобразований можно найти амплитуду
установившихся вынужденных колебаний
силы тока в контуре:
.
Подставляя
это возможное решение в дифференциальное
уравнение, после математических
преобразований можно найти амплитуду
установившихся вынужденных колебаний
силы тока в контуре:
![]() .
.
По
приближенной теории резонанса амплитуда
силы тока максимальна
![]() ,
если
,
если
![]() ,
в этом случае
,
в этом случае
![]() .
А
поскольку по формуле Томпсона
.
А
поскольку по формуле Томпсона
![]() - квадрату собственной частоты незатухающих
колебаний в идеальном контуре (R
= 0), можно говорить о явлении резонанса
— резком возрастании амплитуды
вынужденных колебаний, в случае если
частота периодических внешних воздействий
приближается к собственной частоте
колебательной системы. Чем меньше
активное сопротивление R,
в
котором происходит превращение части
электромагнитной энергии в тепловую
энергию, тем больше максимальная
амплитуда силы тока, тем выше резонансный
пик. Величина
- квадрату собственной частоты незатухающих
колебаний в идеальном контуре (R
= 0), можно говорить о явлении резонанса
— резком возрастании амплитуды
вынужденных колебаний, в случае если
частота периодических внешних воздействий
приближается к собственной частоте
колебательной системы. Чем меньше
активное сопротивление R,
в
котором происходит превращение части
электромагнитной энергии в тепловую
энергию, тем больше максимальная
амплитуда силы тока, тем выше резонансный
пик. Величина
![]() представляет сопротивление
последовательной цепочки C,
L,
R
переменному
току частоты ω.
Полное
сопротивление Z
называют
импедансом
нагрузки. При
резонансе импеданс минимален и поэтому
сила тока максимальна.
представляет сопротивление
последовательной цепочки C,
L,
R
переменному
току частоты ω.
Полное
сопротивление Z
называют
импедансом
нагрузки. При
резонансе импеданс минимален и поэтому
сила тока максимальна.
Более сложна теория вынужденных электромагнитных колебаний, когда переменный ток, имеющий частоту ω, разветвляется по двум ветвям: по конденсатору, катушке индуктивности и резистору (рис. 1б). В этом случае при сближении частот ω и ω0 импеданс достигает максимального значения и поэтому наблюдается резонансный пик для напряжения на контуре.
Описание экспериментальной установки
Колебательный контур, состоящий из катушки индуктивности L (1) и конденсатора C (2), через ограничивающее ток сопротивление R (3), подключен к звуковому генератору (4). Звуковой генератор вырабатывает синусоидальное напряжение, частоту и амплитуду которого можно регулировать. Напряжение на контуре показывает вольтметр (5) магнитоэлектрической системы, включенный в цепь переменного тока через диоды. От контурного конденсатора (2) сделаны отводы к разъемам (6) для подключения дополнительного конденсатора (7) известной емкости.