§24. Термодинамический потенциал Гиббса

В термодинамике есть следующее понятие:

-свободная энергия Гельмгольца

- свободная энергия Гиббса.

-термодинамический потенциал Гиббса, он играет важную роль в связи с большим каноническим распределением.

здесь - статистическая сумма канонического распределения, а - статистическая сумма большого канонического распределения.

Запишем первое начало термодинамики:

Используя большое каноническое распределение, рассчитаем энтропию:

Теперь переходим в термодинамику, т.е. опускаем знак для средних:

Отсюда имеем:

Запишем выражение:

Подставим сюда выражения для первого начала термодинамики, тогда получим:

(17)

Аналогично получим .

Подставим сюда выражение для :

(18)

Нетрудно показать, что

Из соотношений (17) и (18) видно, функциями каких переменных являются функции и :

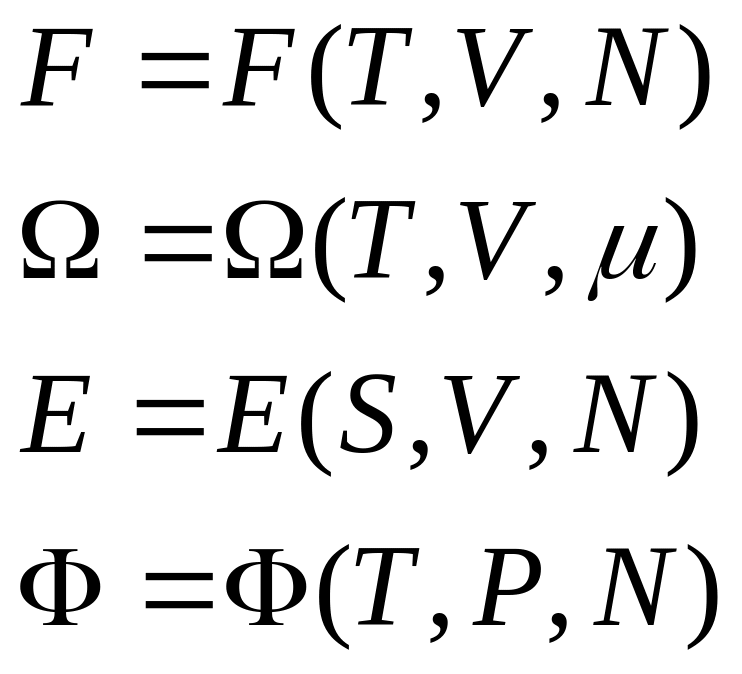
Переход от одной функции к другой идёт с помощью преобразования Лежандра, т.е. переходя от одних переменных к другим.

Из полученных нами выражений вытекают определения:

Из (17) имеем

, здесь

Из (18) имеем:

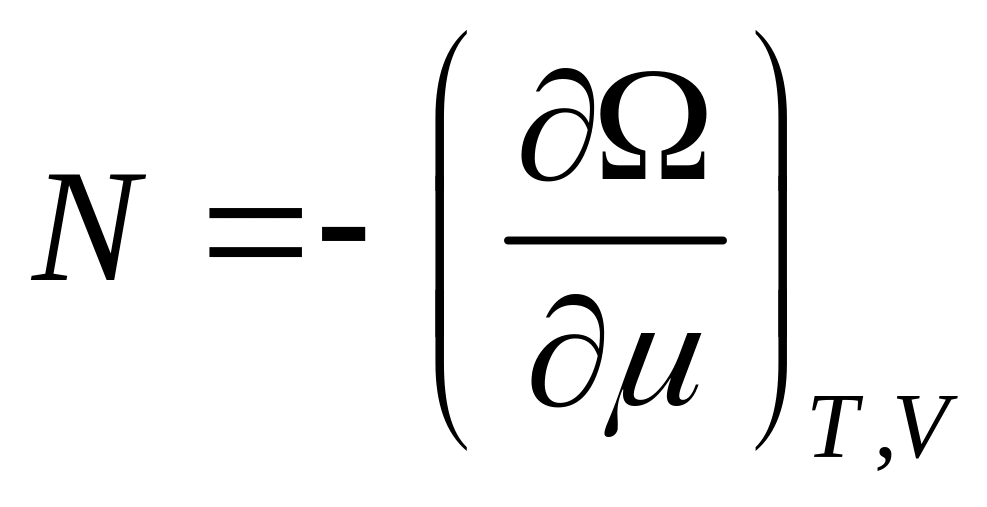, здесь

- это интенсивный параметр, т.е. при равновесии системы он выравнивается.

- это экстенсивный параметр, он аддитивен, поэтому в статистической физике соотношение для пишется так:

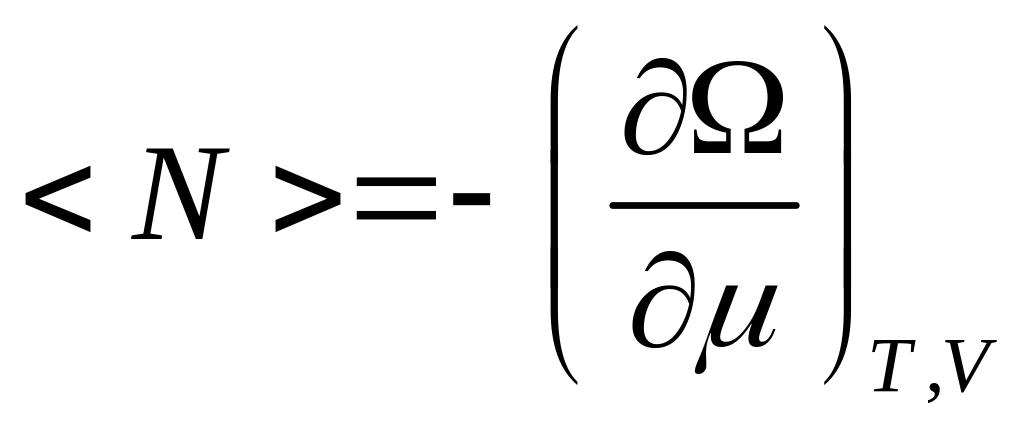
§25. Распределение Ферми-Дирака

Чтобы получить распределение Ферми-Дирака надо посчитать термодинамический потенциал :

- одночастичная большая статистическая сумма.

И с помощью посчитаем число состояний с учетом свойств Ферми-частиц.

Напомним, что:

здесь отсутствует взаимодействие между частицами, но имеет место обменное взаимодействие, т.е. за счёт спина (влияние сорта частиц на результат)

Для Ферми-частиц либо 1.

Рассчитаем для Ферми-газа:

где .

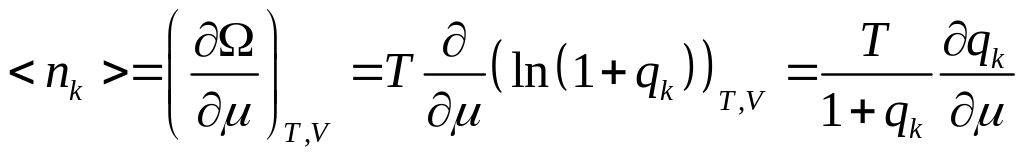
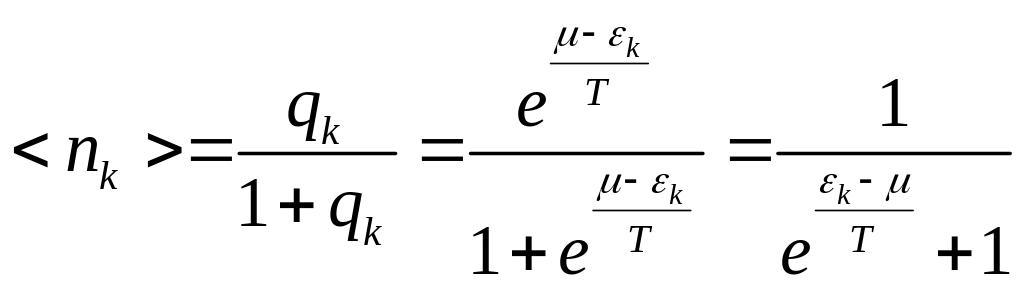
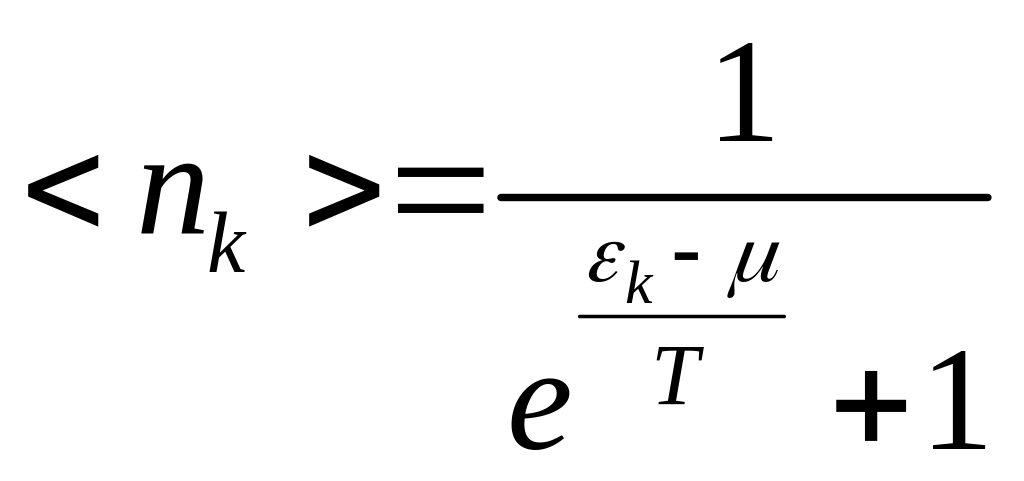
Мы получили распределение Ферми-Дирака. Это среднее число Ферми частиц в -том состоянии.

Придадим другой смысл. По определению:

Таким образом, это вероятность обнаружить одну Ферми частицу в -том состоянии:

§26. Распределение Бозе-Эйнштейна

Используем формулы:

, но здесь

Записав через получим:

Условие сходимости ряда:

равенство нулю реализуется для систем с не сохраняющимся числом частиц, например, для фотонного газа или аннигилирующих частиц.

Получим:

С помощью найдём среднее число частиц в -том состоянии:

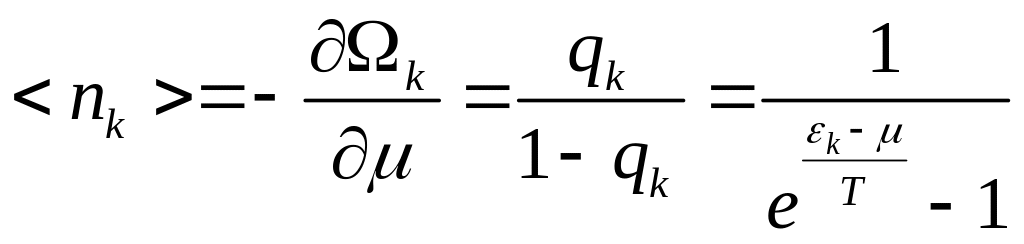
И мы получили распределение Бозе-Эйнштейна.

Теперь можно объединить все три распределения в одну формулу и записать:

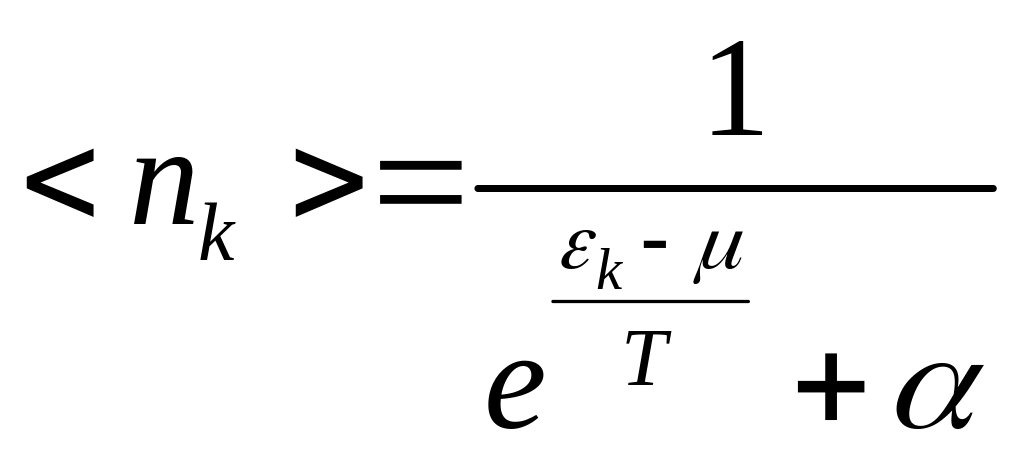
Мы получили выражение для числа частиц в зависимости от сорта частиц, т.е. от спина частиц.

Очевидно, что если выполняется критерий больцмановского распределения:

то все распределения переходят в больцмановское распределение:

Ограничения на химический потенциал:

- для Бозе-Эйнштейна

и - для Больцмана

- произвольный для Ферми-Дирака

§27. Ферми и Бозе газы элементарных частиц

Элементарная частица – значит что квантовые частицы рассматриваются как точки, не учитывая их структуры. Исследуем только поступательное движение этих частиц. В этом и есть смысл слов «элементарная частица».

В этом случае можем воспользоваться квазиклассическим приближением.

Здесь переходим от - номера квантового состояния в фазовое пространство .

это в квазиклассике, когда .

Состояние описывается фазовой точкой в фазовом пространстве. В фазовом пространстве имеем одну точку, т.к. состояние одночастичное.

В фазовом пространстве число частиц:

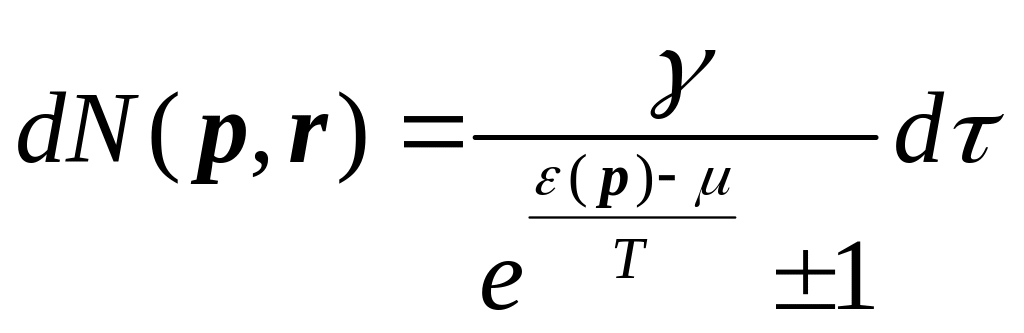
Пишем , т.к. рассматриваем поступательное движение, т.е. следует зависимость только от , а от нет зависимости, наша частица – как точка.

- кратность вырождения по спину

- число одночастичных состояний в элементарном объёме фазового пространства.

Поскольку энергия зависит только от , то можем проинтегрировать по и поставить объём :

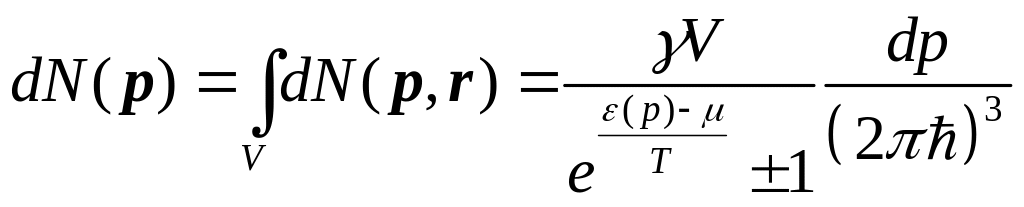
Отсюда можно посчитать полное число частиц в системе и полную энергию системы.

(28)

с помощью этого соотношения преобразуем элементарный объём в импульсном пространстве, используя сферические координаты

Так как функция, стоящая перед не зависит от углов, а зависит только от модуля :

то можем проинтегрировать по углам. Учтем ещё, что:

Используем (28):

Значит:

Тогда число частиц, приходящихся на единичный интервал энергии:

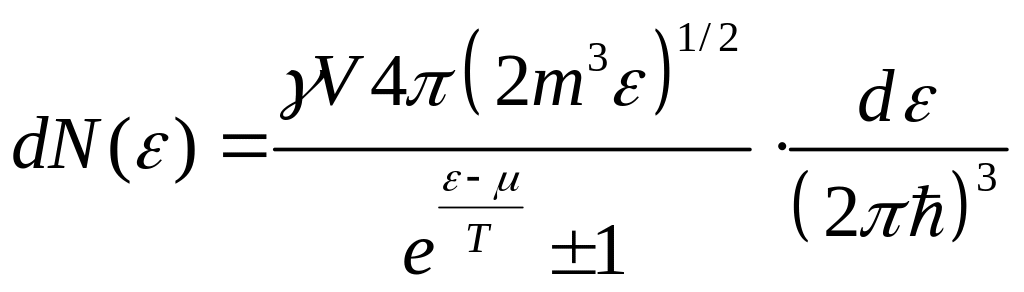
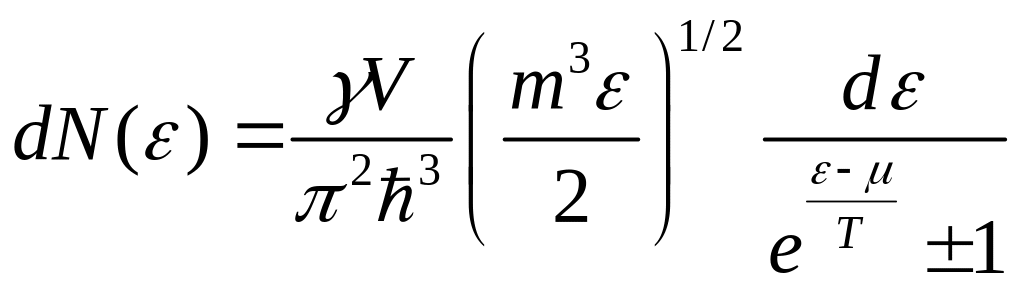
здесь «+» -для Ферми-Дирака, а «-» - для Бозе-Эйнштейна.

Посчитаем среднюю энергию системы и среднее число частиц.

При переходе в термодинамику для наблюдаемых величин пишем:

и

Среднюю энергию и среднее число частиц можно посчитать ещё и таким способом:

- сумма по одночастичным состояниям

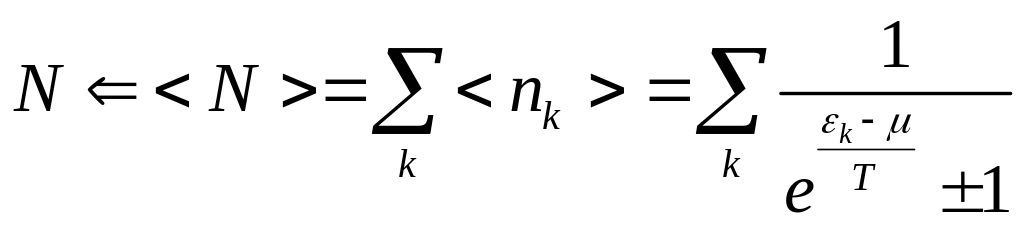
При переходе к квазиклассическому приближению имеем:

Точно так же рассчитывается термодинамический потенциал:

, где

Поэтому при подстановке в имеем:

«+» -для Ферми-Дирака, а «-» - для Бозе-Эйнштейна.

В квазиклассическом приближении получим:

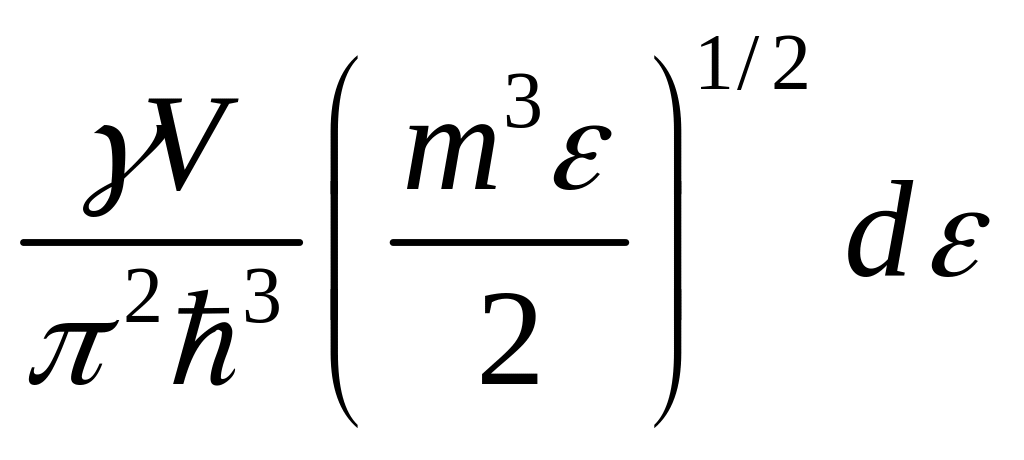- возникло при переходе к квазиклассике в переменные по энергии.

Здесь .