§7. Эргодическая гипотеза

Согласно эргодической гипотезе, для наблюдаемых величин в статистической физике водится:

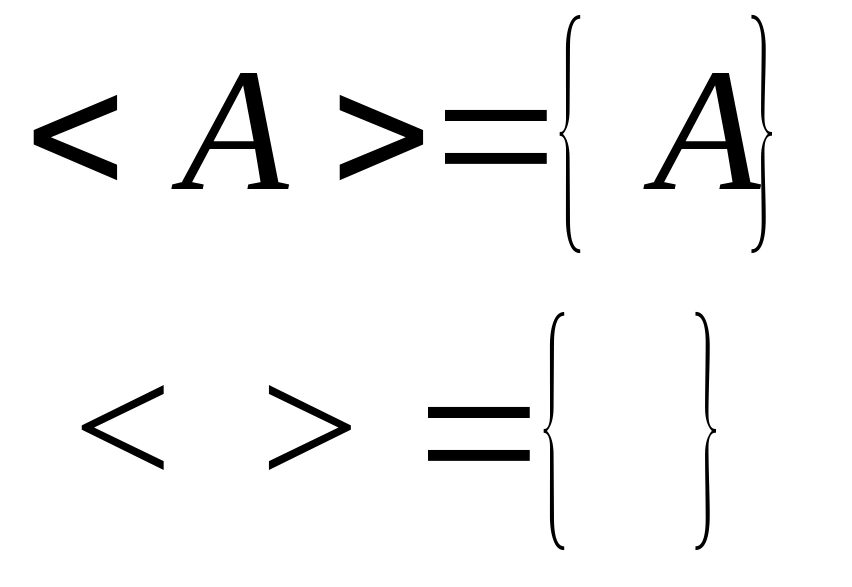
Процессы или поля для которых удовлетворяется это равенство называют эргодическими.

- это усреднение по пространству реализаций, где -случайное поле, т.к. здесь больше одной переменной у

- усреднение по аргументам, которые «сидят» в . - это случайный процесс, т.к. одна переменная в .

§8. Равновесное состояние системы

Для стационарных процессов в случае систем с большим числом степеней свободы обнаруживается (где процесс ), что в процессе измерения величины , она основное время пребывает в состоянии, имеющим значение близкое к числу (которое практически не отлично от ).

Система длительное время пребывает в состоянии со значением . Это значение представляется, таким образом, наиболее вероятным значением случайной величины .

Состояние системы, описываемое наиболее вероятными значениями макропараметра, называется равновесным. Стационарная макросистема основное время пребывает в равновесном состоянии, хотя бывают кратковременные флуктуации.

В термодинамике, во всех термодинамических соотношениях, используются равновесные состояния. Например, под понимают (пишут , а подразумевают ).

§9. Время релаксации

Если система выведена из состояния равновесия, то время, в течение которого она, оставленная без воздействия извне, переходит в равновесное состояние, называется временем релаксации .

Если говорят о достаточно больших временах (малых), то обязательно в сравнении с временем .

Достаточно большая макросистема может быть разбита на подсистемы. Так как подсистемы меньше системы, то время релаксации подсистемы меньше времени релаксации всей системы. Так же можно ввести частичные времена релаксации, т.е. времена релаксации по какому-то параметру системы (например, по температуре, по плотности и т.п.).

Можем иметь неполное или частичное равновесие, если рассматриваемы интервал времени :

Здесь - наименьшее из частичных времен релаксации системы, а - наибольшее из частичных времен релаксации системы.

Неполное равновесие – система по каким-то параметрам пришла в равновесие, а по другим параметрам ещё не пришла в равновесие.

§10. Квазизамкнутость и статистическая независимость подсистем

Р ассмотрим систему состоящую из некоторого числа подсистем.

Даны две подсистемы и их область контакта. Взаимодействие между подсистемами идёт через границу, через приграничный слой в который проникает взаимодействие.

Чем больше время наблюдения, тем глубже проникает взаимодействие в подсистемы. Чем меньше время, тем уже этот слой.

Если слой очень узок, то взаимодействием можно пренебречь, в течение достаточно малого промежутка времени. Такие системы называются квазизамкнутыми.

С точки зрения теории вероятностей вводят понятие статистической независимости.

- обладает свойством мультипликативности, т.е. её можно разбить на произведение элементарных объёмов подсистем:

Здесь - это подсистемы.

В общем случае - немультипликативна. Но для статистически независимых подсистем тоже мультипликативна:

На языке средних:

Здесь - это функция координат -той подсистемы, тогда:

Тогда можно усреднять параметры, относящиеся к переменным данной подсистемы.

Вероятность , тогда тоже разбивается на .

Статистическую независимость обычно рассматривают при .

§11. Принцип равновероятности микросостояний

Бывает необходимо подсчитать число микросостояний, которые отвечают данному макросостоянию. Принцип равновероятности говорит, что все микросостояния, реализующие данное макросостояние, равновероятны (иногда в этом определении добавляют – для замкнутой системы).

§12. Статистический вес макросостояния

Статистический вес макросостояния – это число микросостояний, реализующих данное макросостояние.

§13. Статистическая энтропия

Вводится понятие энтропии:

- на языке плотности вероятности.

- на языке функции распределения.

Оказывается, что

где - статистический вес макросостояния.

§14. Теорема Лиувилля

Утверждается, что функция есть интеграл движения:

С помощью этой теоремы далее делаются выводы, которые приводят к получению функции или .

Если рассматривается случай квантовой статистики, то:

, где ( - это номер состояния)

А среднее:

, где

Из теоремы Лиувилля извлечём свойство:

Так как - интеграл движения, то она может быть представлена через комбинацию имеющихся у системы интегралов движения , т.е. число интегралов движения – конечное число.

Для простоты часто рассматривают так называемое микроканоническое распределение.

В случае квазизамкнутых статистически независимых систем для плотности вероятностей мы писали:

, - число подсистем

И для :

-это следствие статистической независимости подсистем.

Для квантового случая пишут , -индекс подсистемы, - номер квантового состояния.

Тогда , т.е. логарифм от есть величина аддитивная.

Из теоремы Лиувилля имеем:

, - интеграл движения

т.е. можно получить как суперпозицию интегралов движения. Для квазизамкнутых систем (в частном случае) имеем: - интеграл движения, - аддитивная величина.

Тогда можно представить как суперпозицию аддитивных интегралов движения.

В большинстве случаев ограничиваются одним из семи интегралов движения, а именно энергией. Для -ой системы можем записать:

В этом выражении 7 интегралов движения: один в энергии, три в импульсе и три в моменте импульса.

Когда систему помещают в жёсткий ящик, где она не может ни вращаться, ни перемещать, то зависимость от и пропадает, и остаётся:

здесь и - произвольные константы.

В силу макроскопичности системы, влияния граничных условий ящика на общее термодинамическое состояние нет, есть лишь влияние в тонком приграничном слое.

В квантовом случае, можно взять равной , где - это коэффициенты разложения волновой функции по собственным функциям оператора Гамильтониана (оператора энергии).