Непрерывное прямое и обратное вейвлет-преобразования

Основной задачей теории вейвлет преобразований является доказательство того, что прямое и обратное вейвлет преобразования способны обеспечить реконструкцию сигнала, причём точную или хотя бы приближённую, локальную или для сигнала в целом на заданном промежутке времени.

В основе непрерывного вейвлет-преобразования (НВП) лежит использование двух непрерывных и интегрируемых по всей оси t (или x) функций:

• вейвлет-функция psi ψ(t) с нулевым значением интеграла ( ), определяющая детали сигнала и порождающая детализирующие коэффициенты;

• масштабирующая или скейлинг-функция phi φ(t) с единичным значением интеграла ( ), определяющая грубое приближение (аппроксимацию) сигнала и порождающая коэффициенты аппроксимации.

Phi-функции φ(t) присущи далеко не всем вейвлетам, а только тем которые относятся к ортогональным.

Psi-функция ψ(t) создается на основе базисной функции ψ₀(t), которая определяет тип вейвлета. Базисная функция должна удовлетворять всем требованиям, которые отмечены для psi-функции ψ(t). Она должна обеспечить выполнение двух основных операций:

• смещение по оси времени t – ψ₀(t - b) при b R;

• масштабирование - при a>0 и a R⁺ - {0}.

Параметр a – масштабирующий параметр, задаёт ширину этого пакета, а b – параметр сдвига, задаёт его положение. Если a по модулю 0< |a|<<1 то соответствует очень узким окнам, служит для локализованной регистрации высокой частоты соответствующих переходных процессов. Если a по модулю |a|>>1 то это соответствует очень широким окнам и служит для регистрации медленных процессов или длинноволновых колебаний. Шаг растяжения σ>0 (обычно используют σ = 2) задаёт a_j = σ^j (jZ), а параметр сдвига задаётся базовым шагом β>0 (обычно β = 1): b_j,k = k σ^j β (kZ).

Для заданных функций a и b вейвлетом является функция ψ(t):

ψ(t) = . (2)

Видно что любой вейвлет можно сдвинуть и растянуть, а может наоборот сузить во времени. Например для вейвлета функции Гаусса зададим b = 5, а для расширения a = 3. Полученный вейвлет представлен на рис. 5.

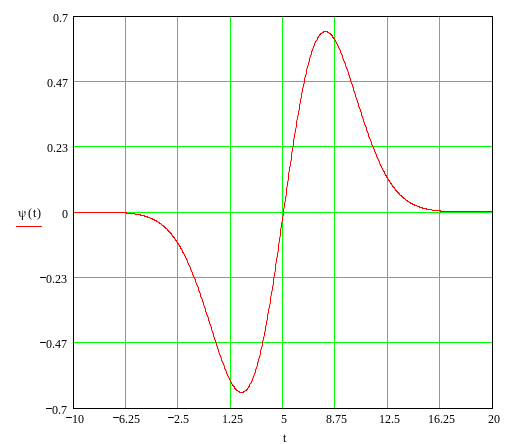
Рисунок 5

Отсюда видно, что вейвлеты это вещественные функции времени t и колеблются вокруг оси t. Базисная функция может быть разнообразной.

Использую вейвлеты можно по аналогии с преобразованием Фурье произвести прямое непрерывное вейвлет-преобразование (ПНВП). Для этого задается сигнал s(t), его энергия конечна в пространстве V с областью ограничения R. Вейвлет-коэффициенты вычисляются по формуле:

C(a,b) = (3,a)

с учётом области ограничения сигналов:

C(a,b) = (3,б)

Вейвлет-коэффициенты определяются интегральным значением скалярного произведения сигнала на вейвлет-функцию заданного вида.

Обратное непрерывное вейвлет-преобразование (ОНВП) осуществляется по формуле реконструкции во временной области:

(4)

где K_ψ – константа, определяемая функцией ψ.

Вейвлет-преобразование способно на основе детализирующей ортогональной вейвлет функции ψ(t) восстановить лишь тонкие детали временной зависимости сигнала s(t). Для восстановления полной формы сигнала приходиться применять аппроксимирующую функцию φ(t).

Анализ с использование функции φ(t) называется кратномасштабным.