2.8 Интегрирование иррациональных функций
2.8.1 Интеграл вида
,
где
–
рациональная функция
Подынтегральная
функция с помощью подстановки
,
,
где
– наименьший общий знаменатель дробей
,
преобразуется в рациональную функцию
от
.
Пример 33.
Найти интеграл
.
Решение.
Сделаем подстановку
,
где 6 – наименьший общий знаменатель
дробей
,
;
найдем
.
Тогда
.
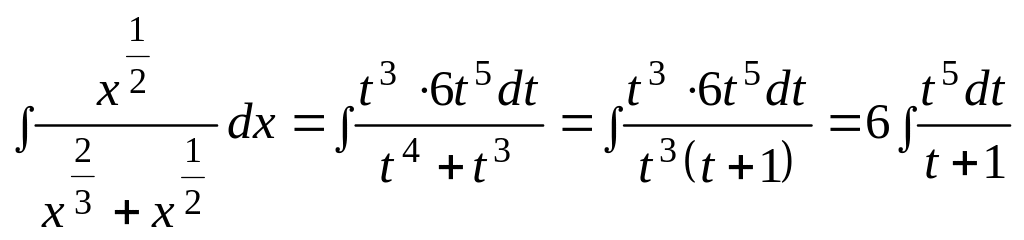Под знаком интеграла – неправильная рациональная дробь. Путем деления числителя на знаменатель выделим целую часть и представим дробь в виде суммы целой части и правильной рациональной дроби:
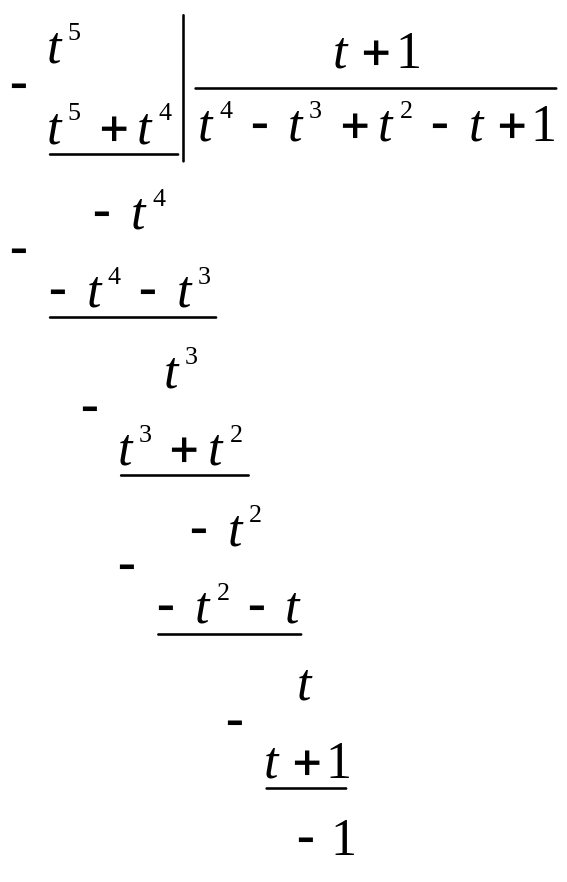
Итак,
.
Тогда
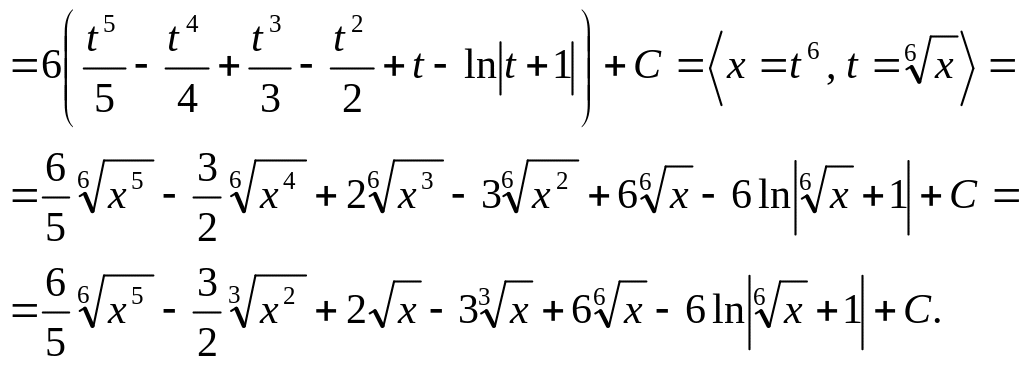
2.8.2 Интеграл вида
Данный интеграл
сводится к интегралу от рациональной
функции с помощью подстановки
,
где
– наименьший общий знаменатель дробей
.
Из данного равенства следует выразить
и найти
.
Пример 34.
Найти интеграл
.
Решение.
Сделаем подстановку
.
Выразим из данного равенства
:
,
,
,
.
Найдем :
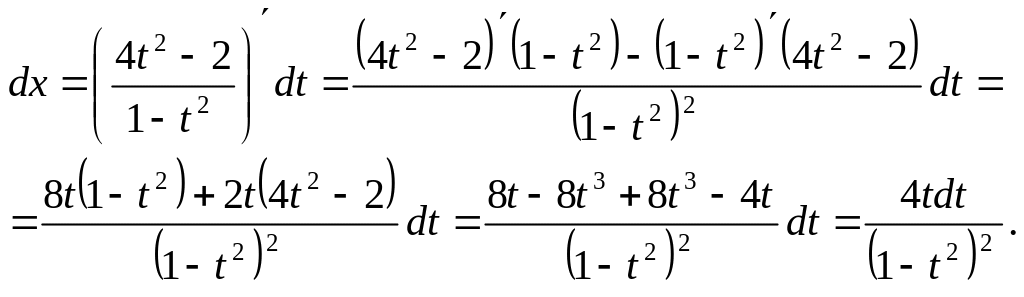
Подставим в интеграл и получим
к
данному интегралу применяем
метод интегрирования по частям:
,
тогда
вернемся
к старой переменной
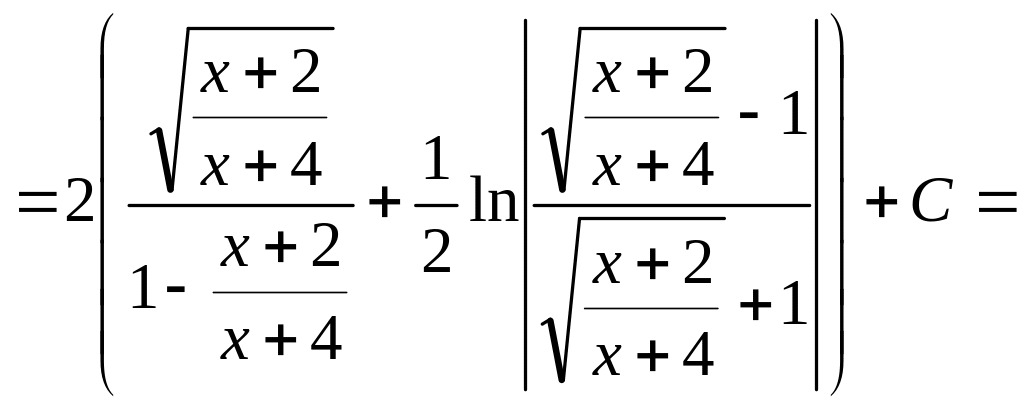
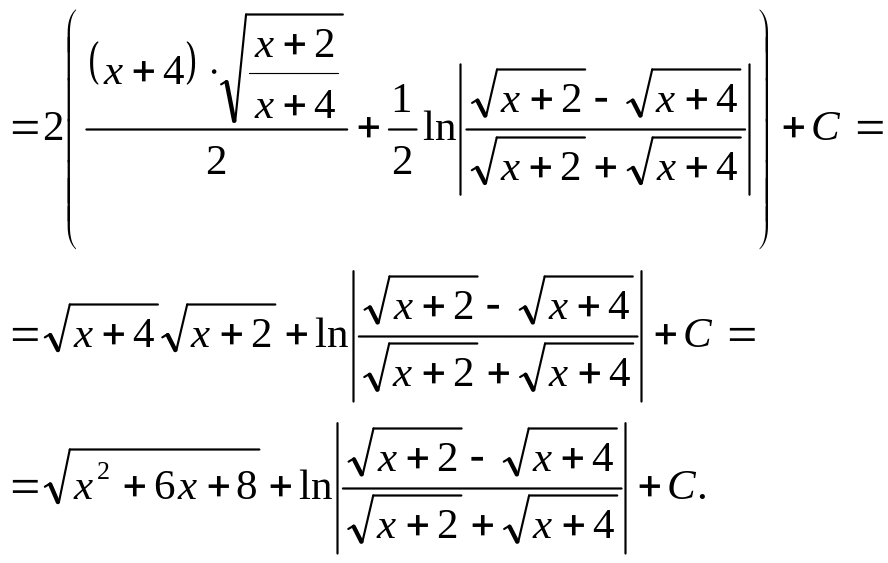
2.8.3 Интегралы
вида
,
,
,
В данных интегралах используют тригонометрические подстановки.
2.8.3.1 ,
,
,
.
Пример 35.
Найти интеграл
.
Решение.
Сделаем подстановку
,
,
,
получим
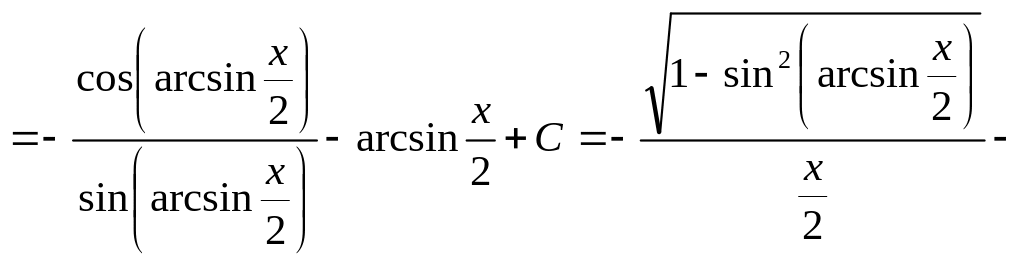
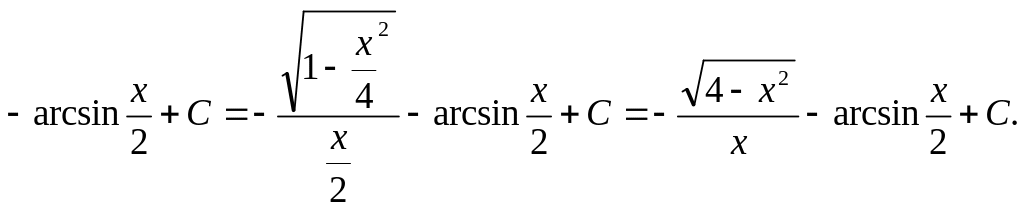
2.8.3.2
,
,
,
,
.
Пример 36. Найти
интеграл
.
Решение.
Сделаем подстановку
,
,
,
.
Тогда
.
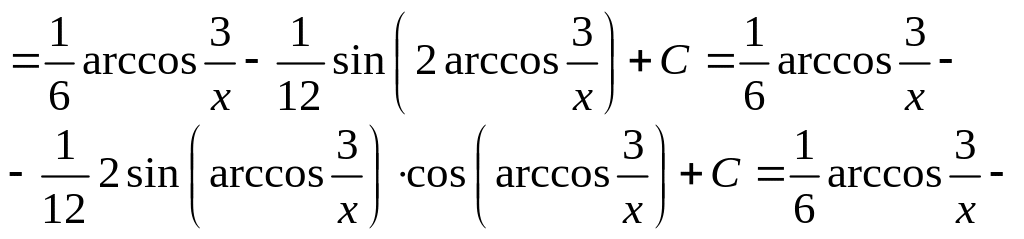
2.8.3.3 ,
,
,
,
.
Пример 37.
Найти интеграл
.
Решение.
Сделаем подстановку
,
,
,
,
получим
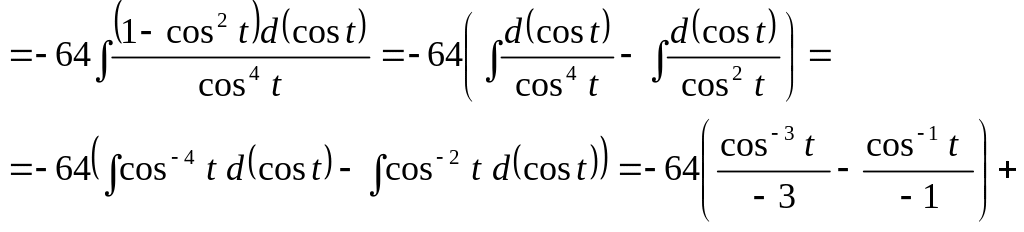
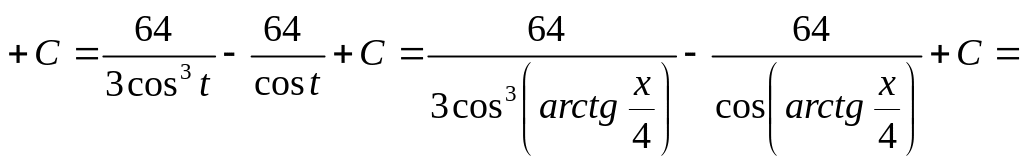
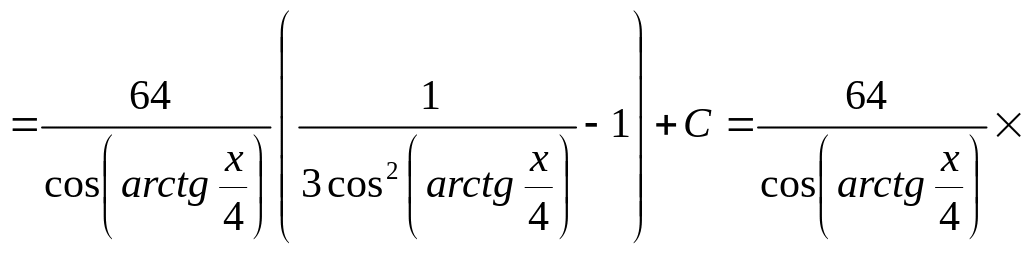
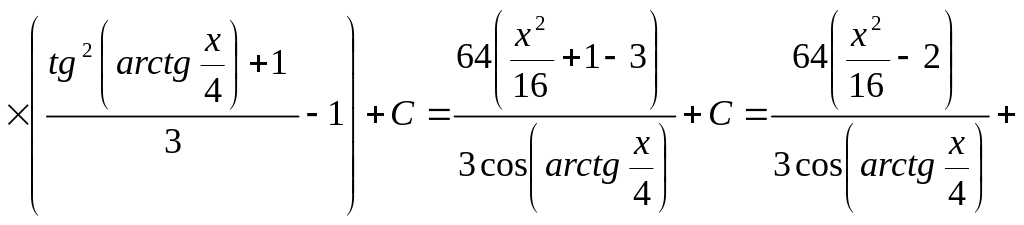
3 Определенный интеграл
3.1 Понятие определенного интеграла
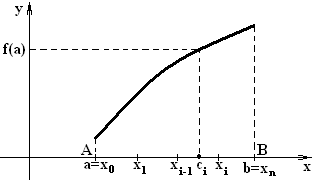
Пусть на отрезке
задана непрерывная функция
(рисунок 1).
|
Рисунок 1 –
График функции
|
Разобьем отрезок
произвольным образом на
частей точками
,
,
,
…,
,
причем
.
Длину частичного отрезка разбиения
обозначим через
,
то есть
.
В каждом частичном отрезке
произвольным образом выберем точку
и найдем значение функции
в каждой точке:
,
,
…,
,
…,
.
Составим сумму
(15)
Данная сумма называется интегральной суммой для функции на отрезке .
Пусть
– длина наибольшего частичного отрезка
разбиения:
.
Найдем предел интегральной суммы при
:
.
Определение 7.
Если
интегральная сумма
имеет предел
,
который не зависит ни от способа разбиения
отрезка
на частичные отрезки, ни от выбора точек
в них, то этот предел называют определенным
интегралом
от функции
на отрезке
и обозначают
.
Таким образом,
,
(16)
где
– нижний предел интегрирования;
– верхний предел
интегрирования;
– подынтегральная функция;
– подынтегральное выражение;
– переменная интегрирования;
– отрезок интегрирования.
Теорема Коши. Если функция непрерывна на отрезке , то определенный интеграл существует.
3.2 Геометрический смысл определенного интеграла
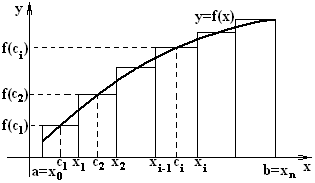
Определение 8.
Фигура, ограниченная сверху графиком
неотри-цательной функции
,
снизу – осью
,
справа и слева – прямыми
и
,
называется криволинейной
трапецией
(рисунок 2).
|
Рисунок 2 – Геометрическая иллюстрация определенного интеграла |
Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
.
(17)
В этом и состоит геометрический смысл определенного интеграла.