2.6.6 Корни знаменателя действительные, среди них есть

кратные

Пример 21. Найти интеграл .

Решение.

а) Разложим знаменатель на простые множители. Методом подбора можно установить, что один корень равен 1, тогда многочлен делится без остатка на :

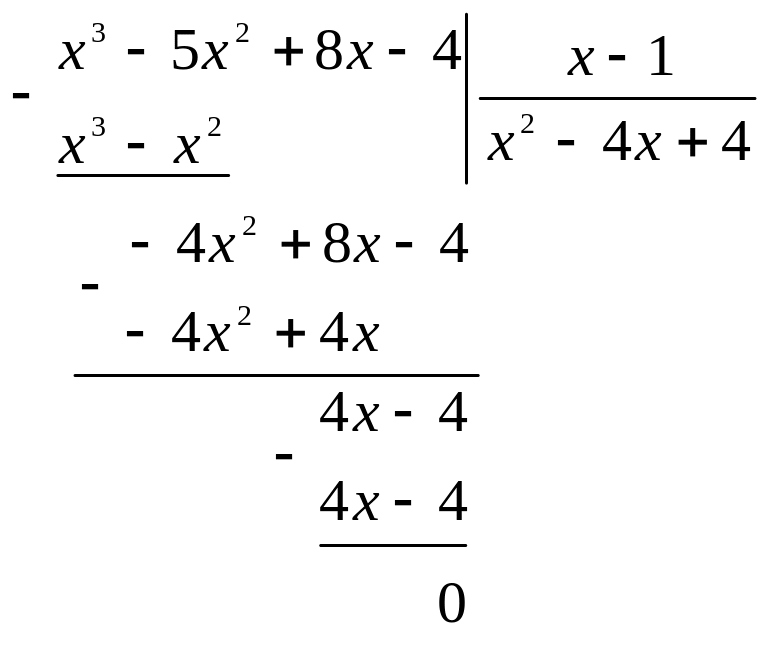
Имеем

.

б) Подынтегральная функция может быть представлена в виде суммы простейших дробей с неопределенными коэффициентами

.

Правую часть приведем к общему знаменателю, получим

.

Приравняем числители, получим тождество

.

Пусть , тогда

, .

Пусть , тогда

, .

Так как действительных корней больше нет, то пусть, например, , тогда

.

В данное равенство подставим известные значения и , найдем : , , .

в) Таким образом,

2.6.7 Корни знаменателя комплексные и различные

Пример 22. Найти интеграл .

Решение. Под знаком интеграла правильная рациональная дробь, так как степень многочлена числителя меньше степени многочлена знаменателя.

Квадратный трехчлен не имеет действительных корней, так как дискриминант . Оба множителя знаменателя не имеют действительных корней, то есть корни знаменателя комплексные, поэтому подынтегральная функция может быть представлена в виде суммы двух простейших дробей

.

Приведем правую часть к общему знаменателю:

.

Данные дроби с одинаковыми знаменателями равны, следова-тельно, тождественно равны их числители

.

Раскроем в правой части скобки и сгруппируем слагаемые с одинаковыми степенями:

.

Два многочлена тождественно равны, когда равны коэффициенты при одинаковых степенях :

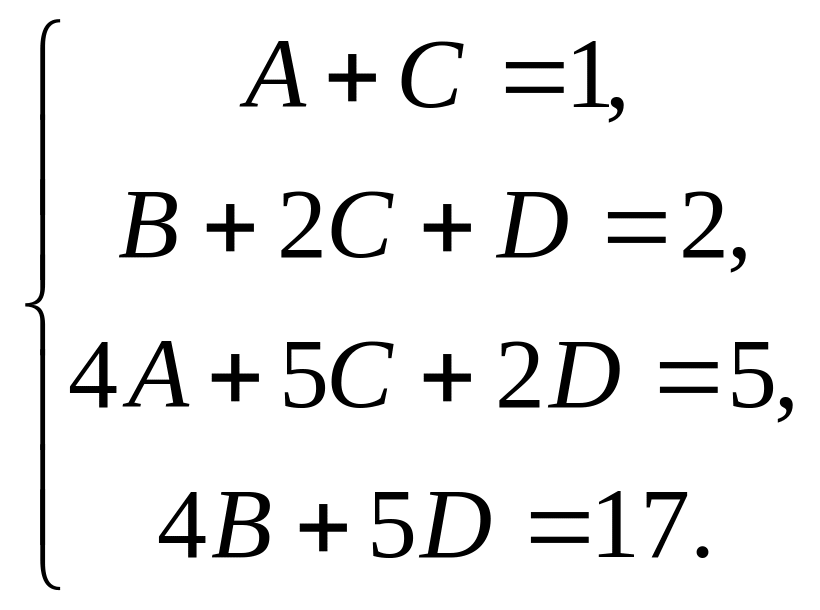
Решим систему методом Гаусса, для этого выпишем расширен-ную матрицу из коэффициентов при неизвестных и свободных членах и сведем ее к ступенчатому виду:

.

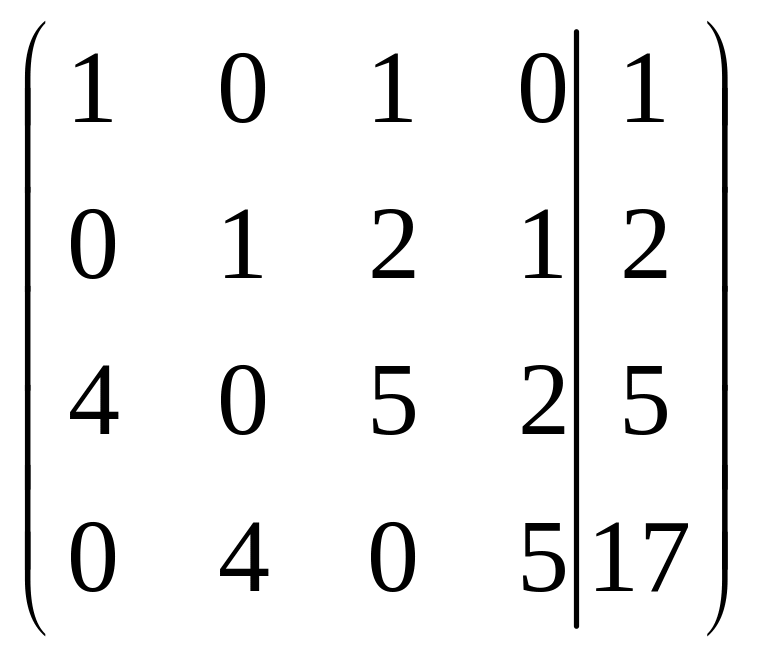Первую строку умножим на и сложим с третьей строкой, вторую строку умножим на и сложим с четвертой строкой, получим матрицу

.

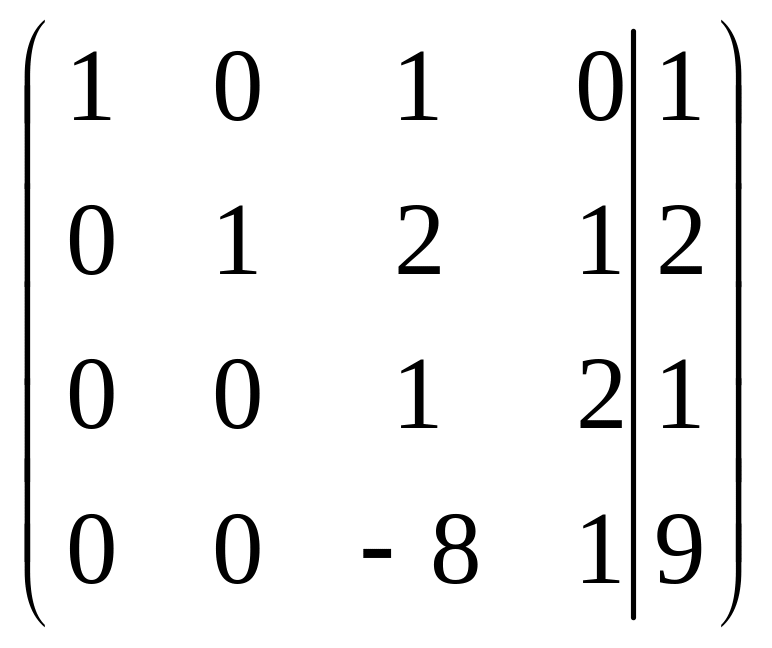Третью строку умножим на 8 и сложим с четвертой строкой, получим матрицу

.

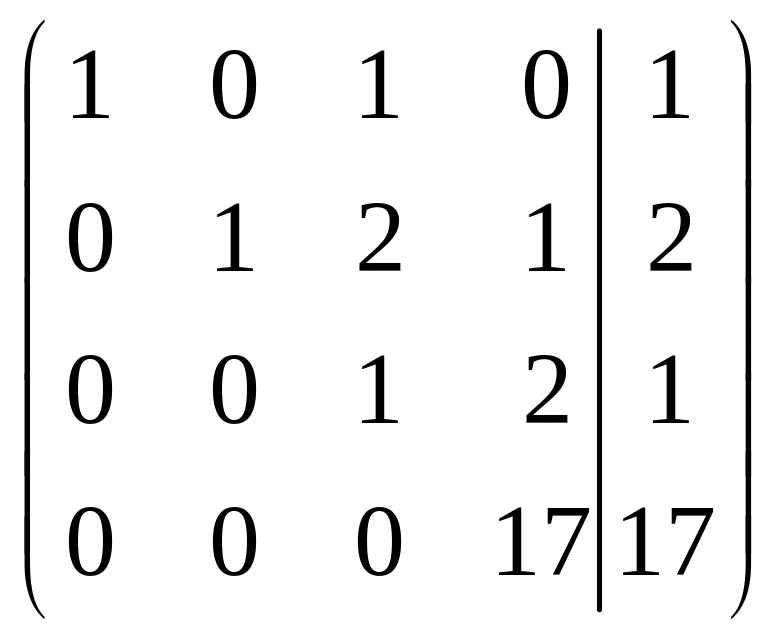Четвертую строку разделим на 17, получим матрицу

.

Запишем систему уравнений для полученной матрицы:

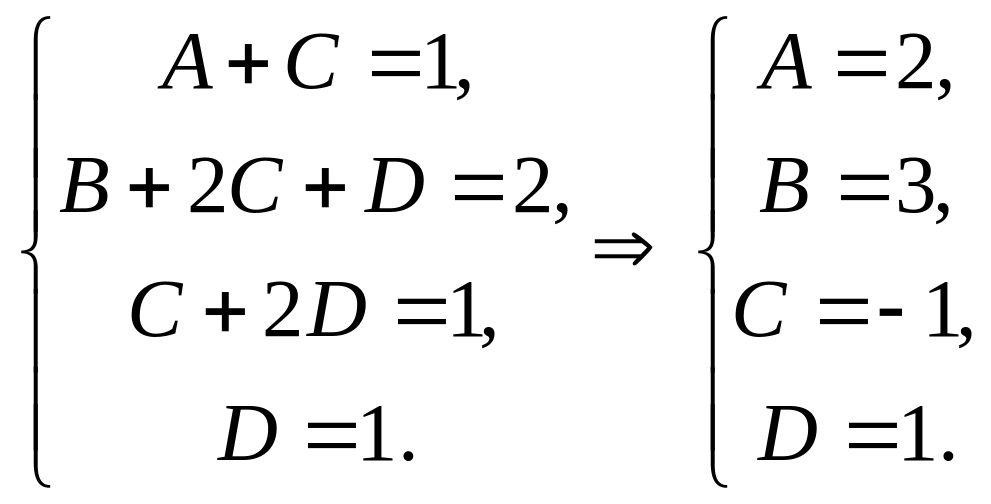
Таким образом, интеграл может быть представлен в виде суммы двух интегралов:

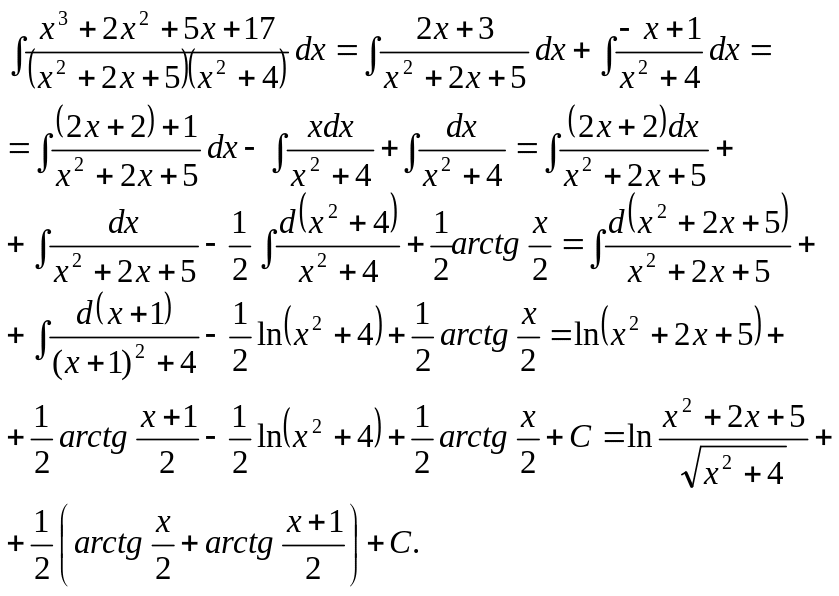
2.6.8 Общий случай

Пример 23. Найти интеграл .

Решение.

а) Рациональная дробь, стоящая под знаком интеграла, неправильная, так как степень многочлена в числителе больше степени многочлена в знаменателе.

Выделим ее целую часть путем деления числителя на знаменатель:

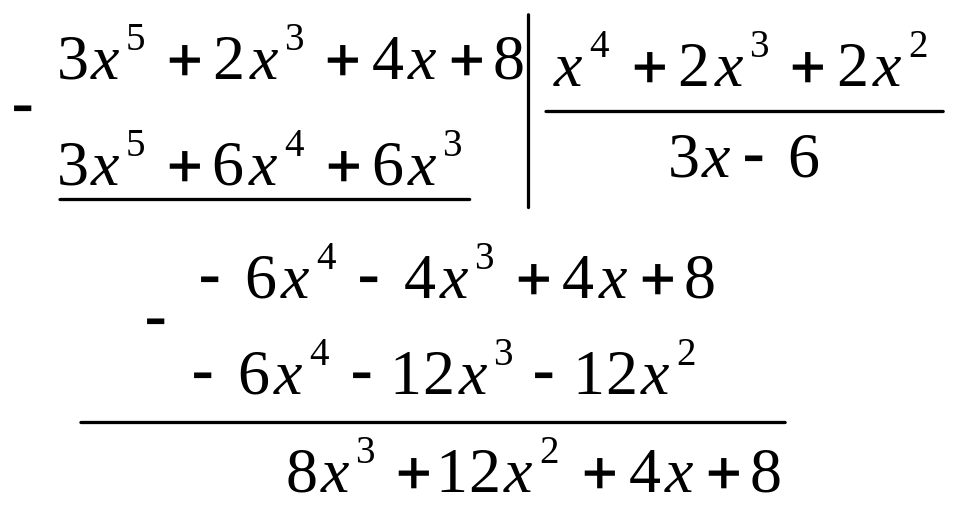
Дробь можно представить в виде суммы целой части и правильной рациональной дроби:

.

б) Разложим правильную рациональную дробь на сумму простейших дробей:

.

Квадратный трехчлен не имеет действительных корней.

в) Правую часть приведем к общему знаменателю, тогда получим

.

Данные дроби равны, если тождественно равны их числители:

.

Преобразуем:

.

Приравниваем коэффициенты при одинаковых степенях :

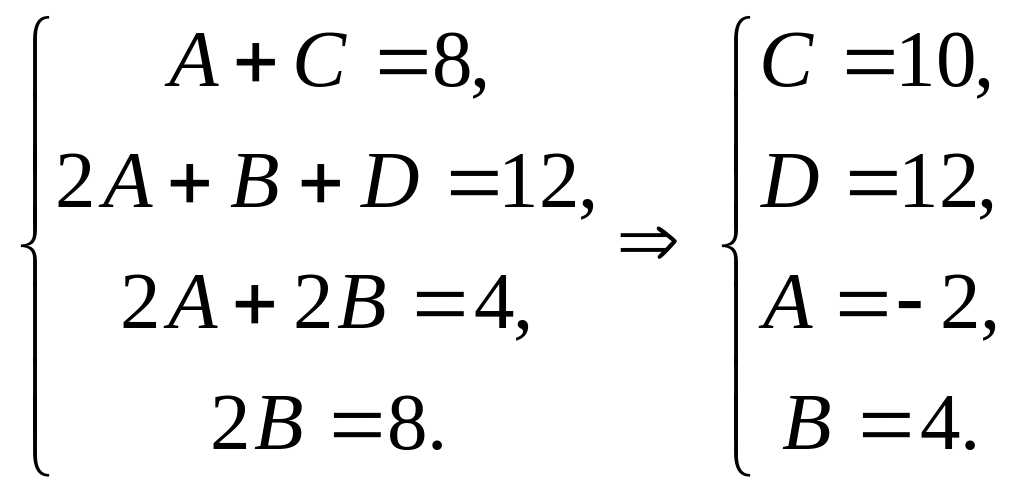
Итак, имеем

.

г) Интегрируем полученное равенство:

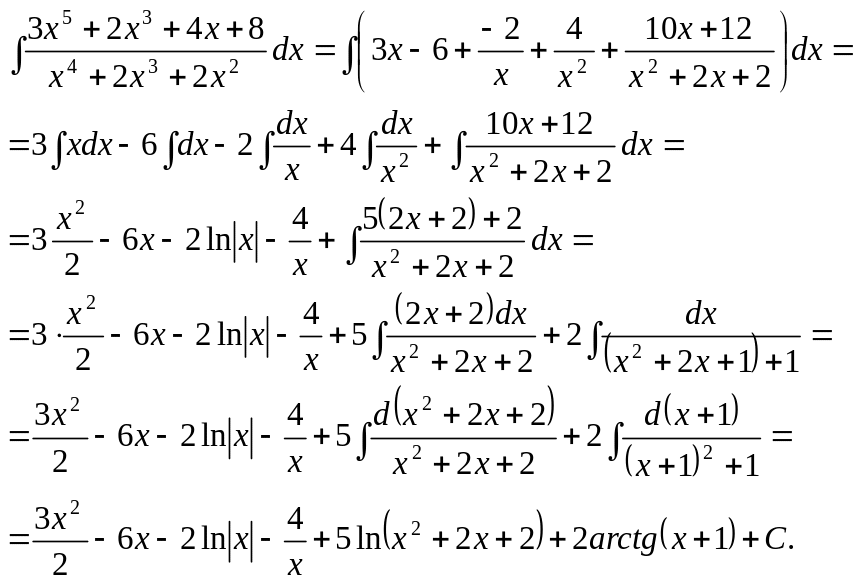
Любая рациональная функция интегрируется в элементарных функциях.

2.7 Интегрирование тригонометрических функций

Рассмотрим некоторые случаи нахождения интеграла от тригоно-метрических функций.