- •Бийский технологический институт (филиал)
- •Неопределенный и определенный интегралы
- •Требования к представлению и оформлению результатов типового расчета
- •1 Неопределенный интеграл
- •Понятие неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •2.2 Метод подведения под знак дифференциала
- •2.3 Метод интегрирования подстановкой
- •2.4 Интегрирование по частям
- •2.5 Интегралы от некоторых функций, содержащих квадратный трехчлен в знаменателе
- •2.5.1 Рассмотрим интеграл
- •2.5.2 Рассмотрим интеграл вида
- •2.5.3 Рассмотрим интеграл вида
- •2.6 Интегрирование рациональных функций
- •2.6.1 Дробно-рациональная функция
- •2.6.2 Правильные рациональные дроби
- •2.6.3 Разложение правильной рациональной дроби на сумму
- •2.6.4 Интегрирование неправильных рациональных дробей
- •2.6.5 Корни знаменателя действительные и различные
- •2.6.6 Корни знаменателя действительные, среди них есть
- •2.6.7 Корни знаменателя комплексные и различные
- •2.6.8 Общий случай
- •2.7 Интегрирование тригонометрических функций
- •Интегралы вида
- •2.7.3 Интегралы вида
- •2.7.4 Интегралы вида
- •2.7.5 Интегралы вида , ,
- •2.8 Интегрирование иррациональных функций
- •2.8.2 Интеграл вида
- •3 Определенный интеграл
- •3.1 Понятие определенного интеграла
- •3.2 Геометрический смысл определенного интеграла
- •3.3 Формула Ньютона–Лейбница
- •Основные свойства определенного интеграла
- •Замена переменной в определенном интеграле
- •3.8.1 Несобственные интегралы с бесконечными пределами
- •3.8.2 Несобственные интегралы от неограниченной функции
- •Приложения определенного интеграла
- •3.9.1 Вычисление площади плоской фигуры
- •3.9.2 Площадь криволинейного сектора
- •3.9.3 Вычисление длины дуги кривой
- •4 Вопросы для самопроверки
- •5 Типовые задания
- •Литература
- •Содержание Требования к представлению и оформлению результатов типового расчета………………………………...3
- •Неопределенный и определенный интегралы
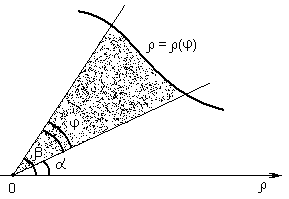
3.9.2 Площадь криволинейного сектора
Область, ограниченная
непрерывной линией
![]() и двумя лучами
и двумя лучами
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() – полярные координаты, называется
криволинейным сектором (рисунок
13).
– полярные координаты, называется
криволинейным сектором (рисунок
13).
|
Рисунок 13 – Криволинейный сектор
|
Площадь криволинейного сектора находится по формуле
![]() .
(35)
.
(35)
Пример 52.
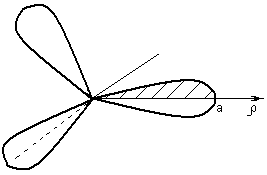
Найти площадь фигуры, ограниченной
«трехлепест-ковой розой»
![]() (рисунок 14).
(рисунок 14).
|
Рисунок 14 – «Трехлепестковая роза»
|
Решение.
Найдем границы изменения величины
:
если
![]() ,
то
,
то
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
а
,
а
![]() ;
если
;
если
![]() ,
то
,
то
![]() или
или
![]() ,
тогда
,
тогда
![]() ,
,
а
,
,
а
![]() .
.
Пусть
![]() ,
тогда значение
изменяется от 0 до
,
тогда значение
изменяется от 0 до
![]() .
Вычислим площадь половины одного
лепестка «розы» и умножим ее на 6.
.
Вычислим площадь половины одного
лепестка «розы» и умножим ее на 6.


![]() (кв.ед.).
(кв.ед.).
3.9.3 Вычисление длины дуги кривой
3.9.3.1 Пусть кривая
![]() на отрезке
задана уравнением
,
тогда дифференциал дуги кривой
на отрезке
задана уравнением
,
тогда дифференциал дуги кривой
![]() .
Интегрируя обе части равенства, получим
формулу для нахождения длины
дуги кривой:
.
Интегрируя обе части равенства, получим
формулу для нахождения длины
дуги кривой:
![]() .
(36)
.
(36)
3.9.3.2 Если кривая
задана параметрическими уравнениями
![]()
![]() ,
то дифференциал дуги кривой
,
то дифференциал дуги кривой
![]() ,
тогда длина
дуги кривой
находится по формуле
,
тогда длина
дуги кривой
находится по формуле
![]() .
(37)
.
(37)
Аналогично для
пространственной кривой, заданной
параметрически
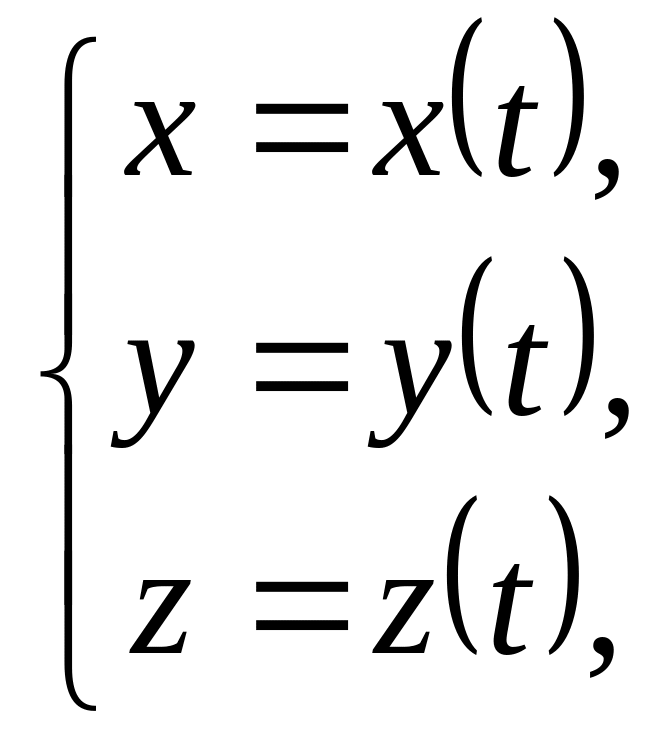 длина дуги
кривой равна
длина дуги
кривой равна
![]() .
(38)
.
(38)
3.9.3.3 Если кривая
задана в
полярной системе координат
,
![]() ,
то дифференциал дуги кривой
,
то дифференциал дуги кривой
![]() ,
а длина дуги
находится по формуле
,
а длина дуги
находится по формуле
![]() .
(39)
.
(39)
Пример 53.
Найти длину дуги кривой
![]() ,
заключенной между точками
,
заключенной между точками
![]() и
и
![]() .
.
Решение.
Кривая
задана в прямоугольной декартовой
системе координат в явном виде. Для
вычисления ее длины воспользуемся
формулой
![]() ,
предварительно вычислив производную
,
предварительно вычислив производную
![]() :
:
![]() .
.
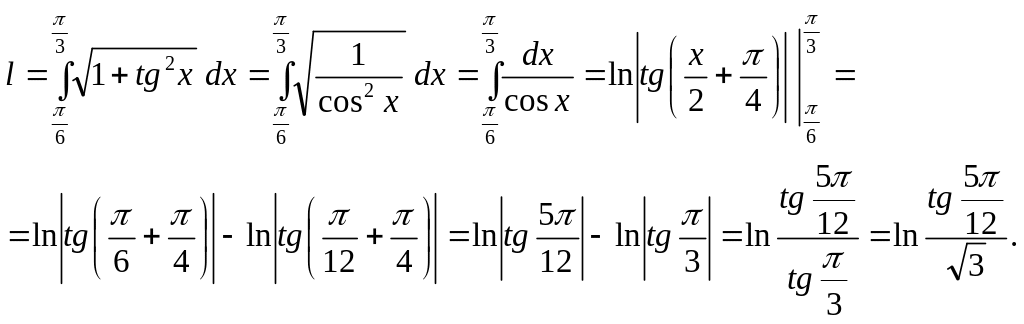
Пример 54.
Найти длину дуги окружности
![]() ,
заключенной между точками
,
заключенной между точками
![]() и
и
![]() .
.
Решение.
Кривая задана параметрически. Для
вычисления ее длины воспользуемся
формулой
![]() ,
предварительно вычислив производные
,
предварительно вычислив производные
![]() и
:
и
:
![]() ,
,
![]() .
.
![]() .
.
Пример 55.
Найти длину дуги кривой
![]() ,
заключенной между лучами
,
заключенной между лучами
![]() и
и
![]() .
.
Решение. Кривая задана в полярной системе координат, поэтому длина дуги вычисляется по формуле
.
Найдем
![]() .
Подставляя в формулу, получим
.
Подставляя в формулу, получим
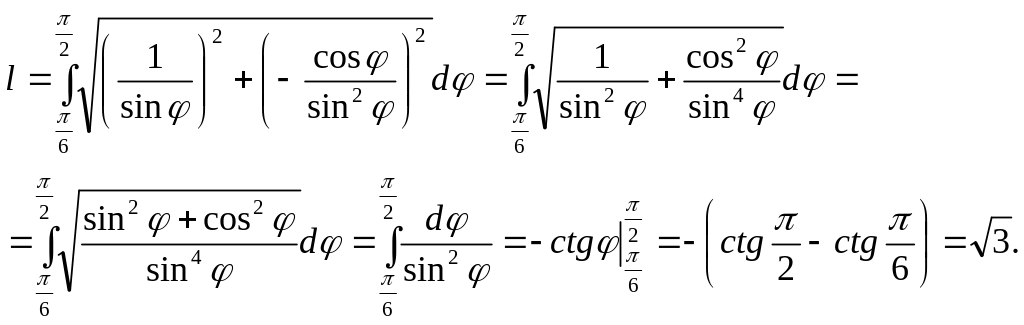
4 Вопросы для самопроверки
Определение первообразной функции. Геометрический смысл совокупности первообразных функций.
Определение неопределенного интеграла.
Основные интегралы.
Свойства неопределенного интеграла.
Основные методы интегрирования:
– метод непосредственного интегрирования;
– метод подведения под знак дифференциала;
– метод интегрирования подстановкой;
– метод интегрирования по частям;
– метод интегрирования дробей, содержащих квадратный трех-член в знаменателе;
– интегрирование простейших рациональных дробей I–IV типов;
– разложение правильной рациональной дроби на простейшие дроби; интегрирование рациональной дроби;
– интегрирование иррациональных функций;
– интегрирование тригонометрических функций.
Определение определенного интеграла, его геометрический и физический смысл.
Свойства определенного интеграла.
Вычисление определенного интеграла. Формула Ньютона–Лей-бница.
Формула замены переменной в определенном интеграле.
Формула интегрирования по частям в определенном интеграле.
Определение несобственного интеграла первого рода.
Определение несобственного интеграла второго рода.
Вычисление площади плоской фигуры.
Вычисление длины дуги кривой.
Вычисление объема тела вращения.
Вычисление площади поверхности вращения.