2.5 Интегралы от некоторых функций, содержащих квадратный трехчлен в знаменателе
К данному методу интегрирования относятся интегралы вида:
1)
; 2)
;
3)
; 4)
.
2.5.1 Рассмотрим интеграл
Преобразуем квадратный трехчлен, выделив полный квадрат:
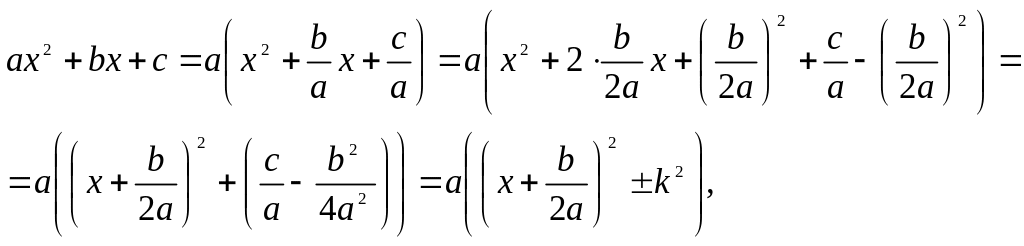
где
.
Таким образом,
интеграл
принимает вид
.
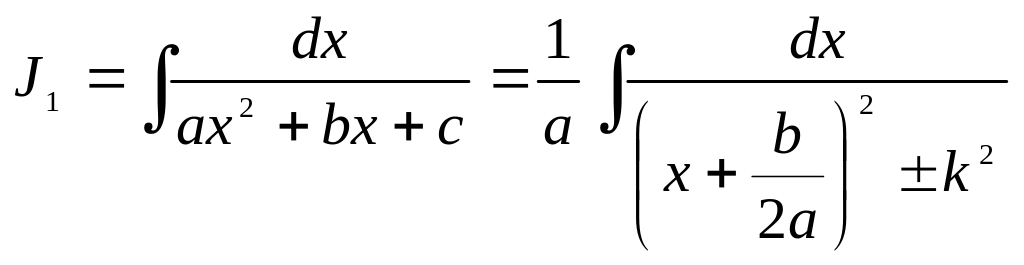Сделаем подстановку
,
.
Тогда получим
.
Это уже табличные интегралы (19 и 20 в п.
1.4).
Пример 15.
Найти интеграл
.
Решение.
,
,
.
2.5.2 Рассмотрим интеграл вида
Преобразуем
подынтегральную функцию: выделим в
числителе производную квадратного
трехчлена
,
получим
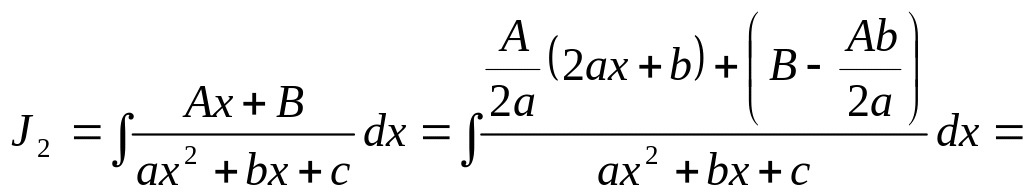
разобьем
на сумму двух интегралов
Пример 16.
Найти интеграл
.
Решение.
Применим указанный прием: выделим в
числителе производную квадратного
трехчлена
и преобразуем числитель:
2.5.3 Рассмотрим интеграл вида
К данному интегралу применим преобразования, рассмотренные в пункте 2.5.1, тем самым сведем интеграл к табличному.
Сделаем подстановку: , и получим интегралы вида:
если
,
то
;
если
,
то
,
где
.
2.5.4
Интеграл вида
находится аналогично
интегралу вида
.
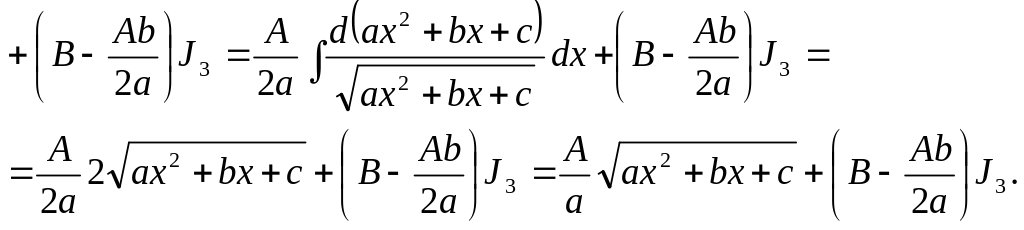
Пример 17.
Найти интеграл
.
Решение.
Выделим в числителе производную
квадратного трех-члена
,
тогда
.
Преобразуем подынтегральную функцию
2.6 Интегрирование рациональных функций
Определение 3. Функция вида
,
где
–
натуральное число,
– постоянные коэффициенты, назы-вается
многочленом
или целой
рациональной функцией.
Число
– степень
многочлена.
Определение 4.
Корнем
многочлена
называется такое значение
,
при котором многочлен обращается в
нуль, то есть
.
Теорема 2.
Если
– корень многочлена
,
то многочлен делится без остатка на
,
то есть
,
где
– многочлен степени
.
Теорема 3 (основная теорема алгебры). Всякий многочлен -й степени имеет, по крайней мере, один корень, действительный или комплексный.
Теорема 4. Всякий многочлен можно представить в виде
,
где
,
,
…,
– корни многочлена;
– коэффициент
многочлена при
.
Теорема 5. Два многочлена тождественно равны друг другу тогда и только тогда, когда коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Теорема 6.
Если многочлен
с действительными коэффици-ентами имеет
комплексный корень
,
то он имеет и сопряженный корень
.
Теорема 7. Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители, дискриминант которых меньше нуля, с действительными коэффициентами, то есть
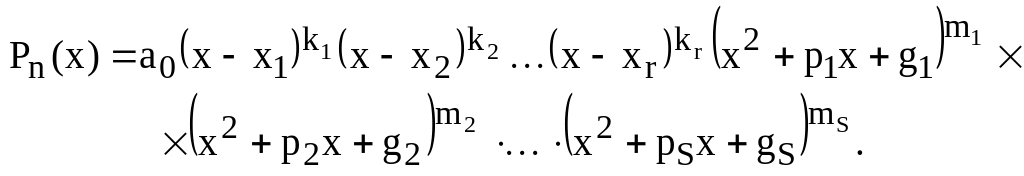
При этом
.
Все квадрат-ные трехчлены не имеют
действительных корней. Например, разложим
на множители многочлены:
;
;
.
2.6.1 Дробно-рациональная функция
Дробно-рациональной функцией называется функция, равная отношению двух многочленов, то есть
,
где
– многочлен степени
;
– многочлен степени
.
Определение 5. Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, в противном случае рациональная дробь называется неправильной.
2.6.2 Правильные рациональные дроби
I)
;
II)
;
III)
;
IV)
.
Определение 6.
Дроби вида
I–IV
называются простейшими
рациональными дробями. Квадратный
трехчлен
не имеет действительных
корней.
Интегрирование простейших дробей вида I–IV не составляет большой трудности.
I) 
.
II)
III)
.
В числителе выделим производную
квадрат-ного трехчлена и преобразуем
числитель:
,
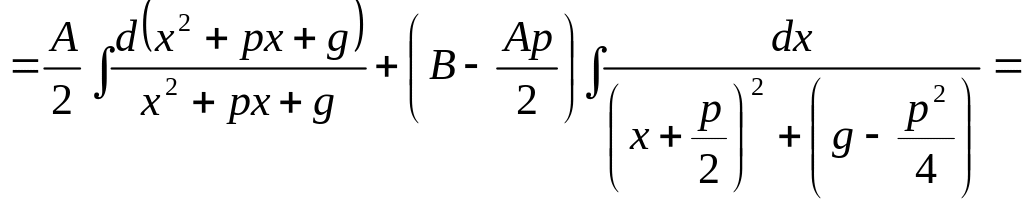
так как квадратный трехчлен не имеет
действительных корней
.
IV)
в
числителе выделим производную квад-ратного
трехчлена
,
тогда
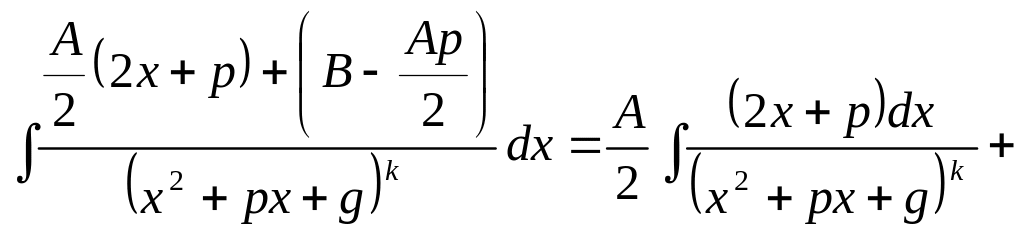
во
втором интеграле выделим полный квадрат
в знаменателе
.
Введем новую переменную
,
обозначим
.
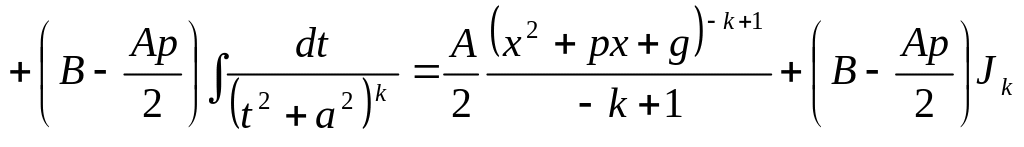Интеграл
берем по рекуррентной формуле
.
Пример 18.
Найти интеграл
.
Решение.
.
Пример 19.
Найти интеграл
.
Решение.
Теорема 8.
Всякую правильную рациональную дробь
,
знаменатель которой разложен на множители
,
можно представить и притом единственным образом в виде суммы простейших дробей:
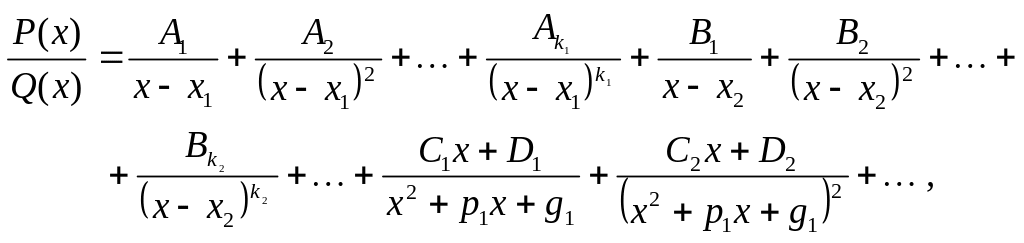
где
,
,
…,
,
,
…,
,
,
…,
,
,
… – некоторые действительные коэффициенты.
1. Линейным множителям
будут соответствовать простей-шие дроби
I-II
типа.
2. Квадратным множителям будут соответствовать простей-шие дроби III-IV типа.
3. Число простейших дробей, соответствующих линейному или квадратному множителю , равно степени, в которой этот множи-тель входит в разложение .