2.3 Метод интегрирования подстановкой

Данный метод заключается во введении новой переменной интегрирования, при этом заданный интеграл приводится к новому интегралу, который является табличным или сводящимся к нему.

Пусть требуется найти интеграл , сделаем подстановку , где – монотонная, имеющая непрерывную производную функция. Тогда и формула интегрирования подстановкой будет иметь вид

. (3)

После нахождения интеграла следует перейти от новой перемен-ной интегрирования к старой переменной .

Пример 8. Найти интеграл .

Решение. Для нахождения данного интеграла сделаем подстановку , тогда

,

.

Интеграл примет вид

= вернемся к старой переменной . Так как , то = .

Используя тригонометрическую формулу

,

преобразуем выражение

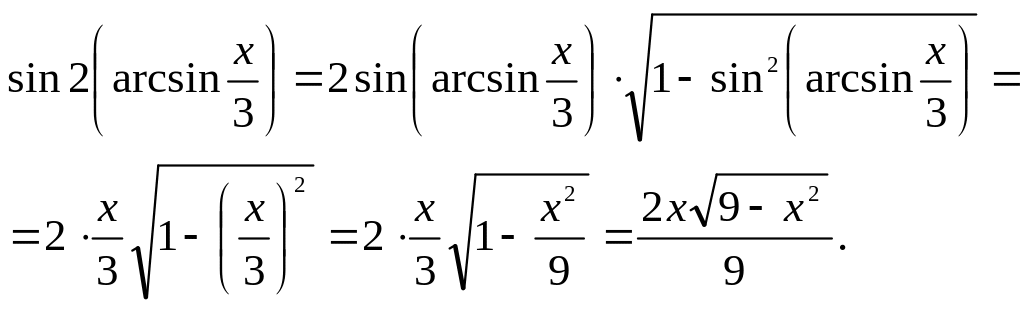
Итак,

Иногда удобно сделать подстановку в виде , тогда получим формулу

.

Пример 9. Найти интеграл .

Решение. Сделаем подстановку , отсюда найдем , .

Итак,

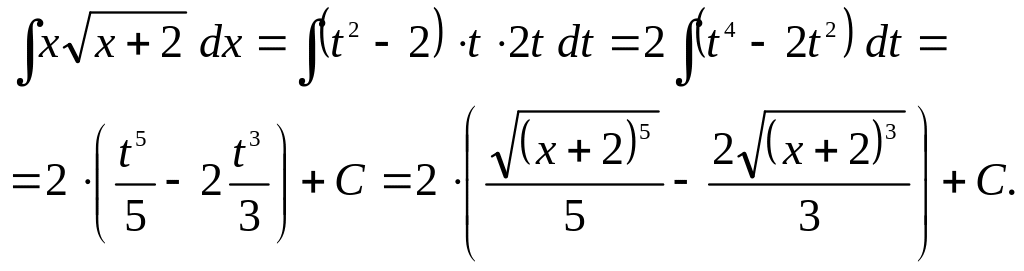
2.4 Интегрирование по частям

Пусть и – дифференцируемые функции. Известно, что дифференциал произведения вычисляется по формуле . Проинтегрируем данное равенство . Используя свойства интеграла, будем иметь , отсюда

. (4)

Данная формула называется формулой интегрирования по частям. Эта формула применяется чаще всего к интегрированию выражений, которые можно представить в виде произведения двух сомножителей и , причем за принимают такой множитель, от которого можно найти интеграл.

Основные виды интегралов, которые берутся по частям, представлены в таблице ( – многочлен степени ).

Таблица 1 ­– Основные виды интегралов, которые берутся по частям

	Интеграл	= (x)	dv
1	2	3	4
I
II
III		В данных интегралах за можно принять любую функцию. Интегрируют два раза и приводят подобные интегралы

Продолжение таблицы 1

1	2	3	4
IV
V

Некоторые другие виды интегралов также можно находить методом интегрирования по частям.

Пример 10. Найти интеграл .

Решение.

тогда

,

Пример 11. Найти интеграл .

Решение.

, , тогда ,

=

Пример 12. Найти интеграл .

Решение.

тогда ,

получим интеграл такого же вида, еще раз необходимо применить интегрирование по частям: , , тогда

,

Получили интеграл первоначального вида. Преобразуем

.

Из данного равенства выразим искомый интеграл

,

отсюда

.

Интегралы такого вида называются круговыми.

Пример 13. Найти интеграл .

Решение.

тогда ,

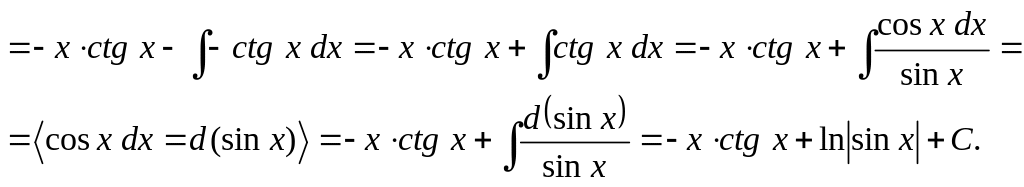
Пример 14. Найти интеграл .

Решение.

тогда ,

.