2. Неравенство треугольника.
Для любых векторов a и b выполнено неравенство:
|a+b|≤|a|+|b|
причем равенство имеет место тогда и только тогда когда a и b коллинеарны.
|a+b|≤|a|+|b| ⇔ |a+b|2≤|a|2+|b|2
(a+b,a+b)≤|a|2+2|a||b|+|b|2
(a,a)+2(a,b)+(b,b) )≤|a|2+2|a||b|+|b|2
(a,b)2≤|a|2*|b|2
Осталось заметить, что последнее неравенство есть уже доказанное неравенство Коши-Буняковского.
3. Линейная независимость лестничной системы векторов.
Рассмотрим в Rn систему векторов специального вида, у которых координаты, стоящие на диагонали не равны нулю, координаты под диагональю – нулевые:
ā1=(a11, a12, a13,…., a1n)
ā2=(0, a22, a23,…., a2n)
ā3=(0,0, a33,….., a3n)
…………………………….
āk=(0, 0, 0, ….., akn)
Доказательство:
Эта система линейно независима (лемма). Для ее доказательства допустим, что система линейно зависима. Тогда первый вектор, у которого нет нулевых координат, может быть выражен через все другие. Но при этом окажется, что его (первого вектора) первая координата равна 0, поскольку первые координаты всех других векторов равны 0. Но первая координата первого вектора не равна 0 по определению, следовательно, наше утверждение о линейной зависимости лестничной системы векторов ложно, а верно обратное, то есть эта система линейно независима, что и требовалось доказать.
4. Однозначность разложения вектора по базису.
Система векторов а1, а2,.. аs называется базисом линейного пространства V, если выполнены следующие условия:
1) эти векторы линейно независимы
2) любой вектор а из Vявляется линейно комбинацией векторов данной системы, т.е. вектор а = к1а1 + к2а2 +…+ кsаs
Размерность подпространства называется рангом системы векторов а1, а2,.. аs и обозначается rk (а1, а2,.. аs). Таким образом, ранг системы равен r, если среди векторов системы существуют r линейно независимых, а любые q > r векторов данной системы линейно зависимы. Ранг же линейно независимой системы равен числу ее членов.
5. Формула умножения комплексных чисел в тригонометрической форме.
При умножении комплексных чисел их модули умножают, а аргументы складывают. Другими словами, если:
z=|z|(cos(φ)+isin(φ), w=|w|(cos(ψ)+isin(ψ), то
zw=|z||w|(cos(φ+ ψ)+isin(φ+ ψ))
Доказательство:
zw=|z|(cos(φ)+isin(φ))*|w|(cos(ψ)+isin(ψ)= |z||w|(cos(φ)cos(ψ)- sin(φ)sin(ψ))(sin(φ)cos(ψ)+ sin(ψ)cos(φ))= |z||w|(cos(φ+ ψ)+isin(φ+ ψ)).
6. Формула деления комплексных чисел в тригонометрической форме.
При делении комплексных чисел их модули делят, а аргументы вычитают. Другими словами, если
z=|z|(cos(φ)+isin(φ), w=|w|(cos(ψ)+isin(ψ), то
z/w=|z|/|w|(cos(φ- ψ)+isin(φ- ψ))
Доказательство:
z/w=z*w-1=|z|(cos(φ)+isin(φ))*|w|-1(cos(-ψ)+isin(-ψ)= |z|/|w|(cos(φ- ψ)+isin(φ- ψ))
7. Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений.
x,z⋲R
При наличии хотя бы одного свободного неизвестного, система имеет бесконечное множество решений. Если свободных решений нет (все неизвестные базисные), то решение единственно.
8. Теорема о пространстве решений однородной системы линейных алгебраических уравнений.
Множество
решений системы однородных уравнений
образует линейное
подпространство
пространства
An.
Размерность
этого подпространства равна
,
а фундаментальная система решений
образует его базис.
1).
2).
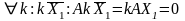
9. Теорема о связи общих решений неоднородной и однородной систем линейных алгебраических уравнений.
Общее решение неоднородной системы линейных алгебраических уравнений равно сумме какого-то частного ее решения и общего решения соответствующей однородной системы.
10. Формулы Крамера для системы двух линейных уравнений с двумя переменными.
Пусть
дана система:
Или в матричной записи: AX=B, где
A=
,
X=
,
B=
Предположим, что матрица A является невырожденной: |A|≠0.
Тогда существует обратная матрица A-1, равная
(1/|A|)*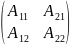
.
Умножив обе части уравнения слева на A-1, получим:
X=A-1B=(1/|A|)*
*
Т.е. x1=(1/|A|)*(A11b1+A21b2)
X2=(1/|A|)*(A12b1+A22b2)
Полученные выражения для неизвестных допускают интересную интерпретацию. Рассмотрим наряду с матрицей A еще две матрицы:
A1=
;
A2=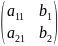
- каждая из них получается из A заменой соответствующего столбца столбцом B. Тогда будем иметь:
|A1|=b1A11+b2A21
(разложение определителя |A1| по первому столбцу) и
|A2|=b1A12+b2A22
Таким образом, x1=|A1|/|A|, x2=|A2|/|A|.