4.1.1 Матричные игры с нулевой суммой

Основная задача теории игр состоит в нахождении таких способов ведения игры для каждого игрока, которые в максимальной степени и с гарантией обеспечивают их интересы при любых ответных действиях противника. Возможные варианты (исходы) игры можно свести в прямоугольную таблицу, называемую платежной матрицей. Рассмотрим игру, которая задана платежной матрицей произвольного порядка m n.

Стратегии игрока В

Стратегии

игрока А

(1)

Строки этой таблицы соответствуют стратегиям выигрывающего игрока А, столбцы соответствуют стратегиям проигрывающего игрока В. Деление участников игры на выигрывающих и проигрывающих является условным, поскольку выигрыши могут быть выражены положительными и отрицательными числами. Положительный выигрыш для игрока А означает его действительный выигрыш, а отрицательный — его проигрыш. В результате выбора пары стратегий ( А_i, В_k ) игрок А получает от В выигрыш а_ik, который указан в платежной матрице на пересечении i-й строки и k-го столбца.

Два игрока независимо друг от друга называют номер строки и номер столбца. На пересечении определяется выигрыш. На этом заканчивается одна партия игры. В следующей партии игры снова происходит выбор строки и столбца. В теории игр предполагается, что разыгрывается не одна, а целый ряд партий. При большом количестве сыгранных партий игрок А стремится получить от игрока В как можно больший средний выигрыш при любых ответных действиях В, а игрок В стремится воспрепятствовать этому и проиграть как можно меньше, так чтобы средний проигрыш был минимальным при любых ответных действиях игрока А.

Матричные игры с седловой точкой

Пример 1. Игра задана платежной функцией следующего вида:

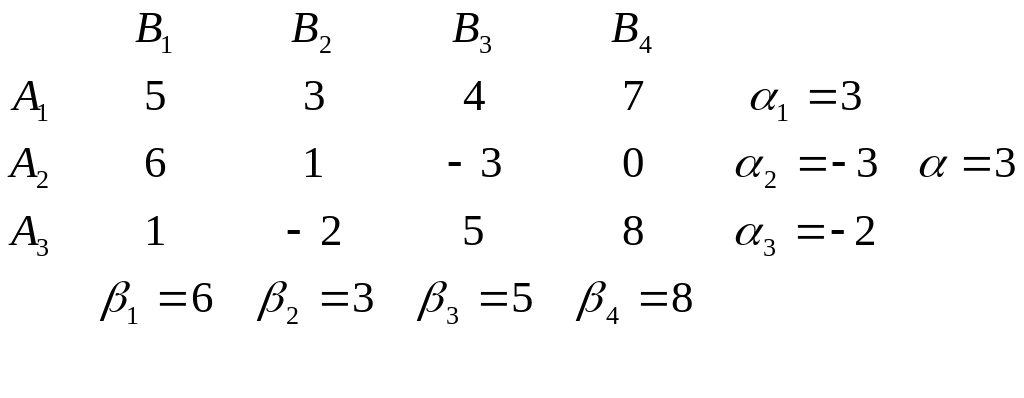
 = 3

По каждой строке определяем минимальное число i и из них выбираем максимальное. По каждому столбцу определяем максимальное число j и из них выбираем минимальное.

Максимальный гарантированный выигрыш игрока А совпадает с минимальным гарантированным проигрышем игрока В и равен  =  = 3 единицам. Это число является наименьшим в своей строке и наибольшим в столбце. Такой элемент матрицы называется седловой точкой.

 = max _i = max min _ij  = min _j = min max _ij

i j j i

Стратегия, которая доставляет игроку А максимальный гарантированный выигрыш равный , называется максиминной стратегией игрока А. Величина  называется нижней ценой игры. Стратегия, которая доставляет игроку В минимальный проигрыш равный , называется минимаксной стратегией игрока В. Величина  называется верхней ценой игры. Важное свойство экстремальных стратегий в играх с седловой точкой состоит в том, что отклонение от экстремальной стратегии только одного игрока А может ухудшить положение отклонившегося.

Для произвольной платежной матрицы нижняя цена игры не превосходит верхней цены игры:  . Решение игры, то есть нахождение наилучших способов ведения игры производится по-разному, в зависимости от того, будет ли  =  или  < . Если  = , то их общее значение  =  = V называется ценой игры.

Матричные игры без седловой точки

Пример 2. Игра задана платежной матрицей следующего вида:

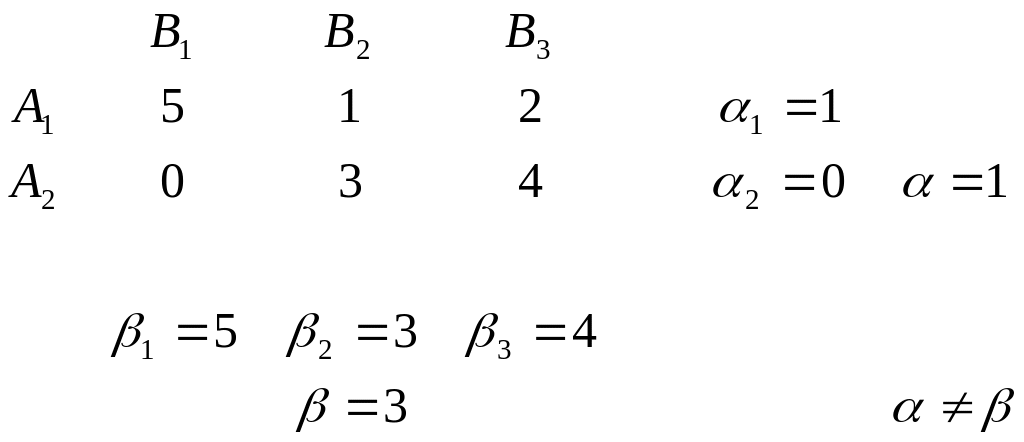
Поскольку  < , седловой точки у матрицы нет.

Решение матричной игры можно упростить, выявив доминирование одних стратегий над другими. Поскольку игрок В заинтересован в минимизации проигрыша, доминирующим будет столбец с наименьшими элементами. Игрок А заинтересован в максимизации выигрыша, доминирующей будет строка с наибольшими элементами.

Пример 3.

1 0 3 5

Н = 3 2 4 3

0 1 -1 4

В матрице Н для игрока В заведомо невыгодной является четвертая стратегия, так как все значения а_i4 превышают соответствующие значения элементов первого и второго столбца. Четвертый столбец матрицы можно исключить (игрок В никогда не воспользуется этой стратегией).

Смешанной стратегией игрока называется случайное чередование отдельных (чистых) его стратегий и применение каждой из них с определенной вероятностью. Смешанную стратегию игрока А, состоящую в применении его чистых стратегий , ,..., с вероятностями p₁, p₂, ..., p_m будем обозначать вектором P = ( p₁, p₂, ..., p_m ). Аналогично для игрока В будем обозначать вектором Q = ( q₁, q₂ ,..., q_n ).

Очевидно, что p_i  0 и q_k  0 при (i = 1, 2, ..., m; k = 1, 2, ..., n)

р₁ + р₂ + ... + р_m = 1

q₁ + q₂ + ... + q_n = 1

Применение игроком только одной чистой стратегии можно рассматривать как частный случай смешанной стратегии, в которой вероятность применения стратегии равна единице, а вероятность применения остальных чистых стратегий равна нулю.

Математическое ожидание выигрыша игрока зависит от матрицы игры и от избранных игроками стратегий. Функция f(P,Q) называется платежной функцией игры. Если известны смешанные стратегии P и Q, то можно найти среднее значение выигрыша, который получает игрок А от В при многократном повторении игры.

Стратегии P* и Q* называются оптимальными, если выполняется следующее соотношение:

f (P,Q*)  f (P*,Q*)  f (P*,Q)

Значение платежной функции f(P*,Q*) при применении игроками своих оптимальных стратегий представляет собой наибольший гарантированный выигрыш игрока А и одновременно наименьший гарантированный проигрыш игрока В. Эта величина называется ценой игры.

V = f (P*,Q*)

Пара оптимальных стратегий P*,Q* каждого игрока и цена игры V называется решением игры.

Основная теорема теории игр утверждает, что всякая матричная игра имеет решение в смешанных стратегиях. Игра может иметь бесконечно много решений, но цена игры всегда определяется однозначно.

Свойства цены игры и оптимальных стратегий

1.   V  

2. Если ко всем элементам платежной матрицы прибавить любое число, то оптимальные стратегии игроков останутся прежними, а цена игры изменится на величину С и будет равна: V + C.

3. Для того чтобы смешанные стратегии P и Q были оптимальными для игроков А и В, необходимо и достаточно выполнение неравенств:

Если игрок А применяет оптимальную смешанную стратегию P_i*, а игрок В любую чистую стратегию , то выигрыш игрока А будет не меньше цены игры. Если игрок В использует оптимальную смешанную стратегию Q*, а игрок А любую чистую стратегию , то проигрыш игрока В не превысит цены игры.

Для примера 2 запишем:

Последовательность действий при решении матричных игр с нулевой суммой:

1. Нахождение нижней цены игры.

2. Нахождение верхней цены игры.

3. Если  = , то решение игры найдено и равно V.

4. Если седловой точки нет, то есть   , тогда цена игры находится в пределах:   V  . Необходимо найти оптимальные смешанные стратегии каждого игрока и цену игры.

5. Сокращение, если возможно, размерности матрицы, то есть удаление дублирующих и доминируемых строк и столбцов. В играх с природой стратегии природы сокращать нельзя. Можно сокращать лишь стратегии лица принимающего решения (ЛПР).

6. Решение на компьютере (в MS Excel).

7. Формулировка выводов на основании полученных результатов.