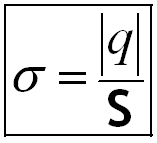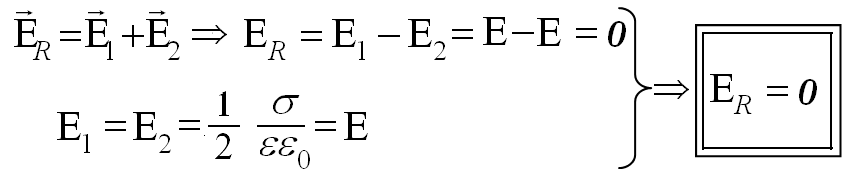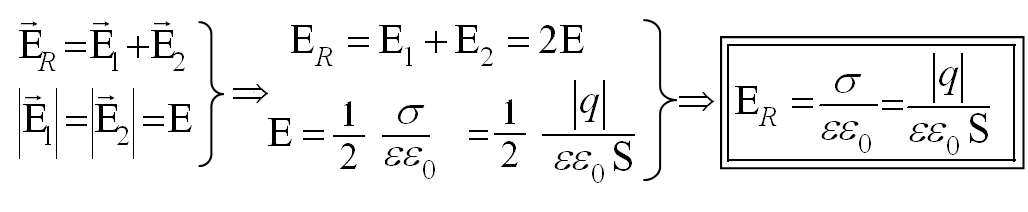Модуль вектора напряжённости поля равномерно заряженной сферы (проводящего шара)
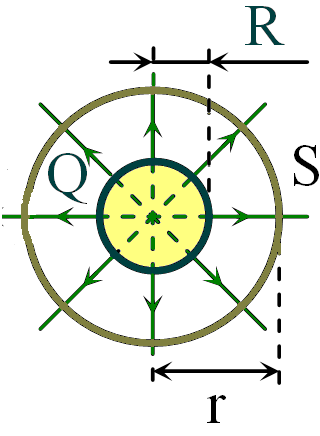
Пусть имеется равномерно заряженная сфера радиуса R и с общим зарядом Q. Благодаря равномерному распределению заряда по поверхности сферы поле, созданное ей, обладает сферической симметрией. Поэтому линии напряженности этого поля направлены радиально. Мысленно окружим данную сферу замкнутой поверхностью в виде сферы радиуса r, имеющую общий центр с заряженной сферой. |
|
|
|
Рассчитаем модуль вектора напряжённости поля заряженной сферы, используя теорему Остроградского ─ Гаусса.
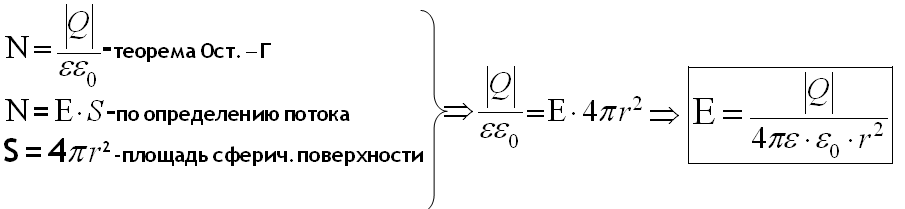
где
r – расстояние от центра заряженной сферы (шара) до точки, в которой определяется модуль напряжённости поля;
Q – заряд сферы (шара).
При r
>R
поле убывает с расстоянием по такому
же закону, как у точечного заряда. Если
r
< R,
то внутри
замкнутой поверхности заряда не будет
и тогда, согласно теореме Остроградского
─ Гаусса, внутри равномерно заряженной
сферы (проводящего шара) напряженность
поля равна
нулю
,
то есть электростатическое поле
отсутствует.
Модуль напряжённости поля равномерно заряженной бесконечной плоскости
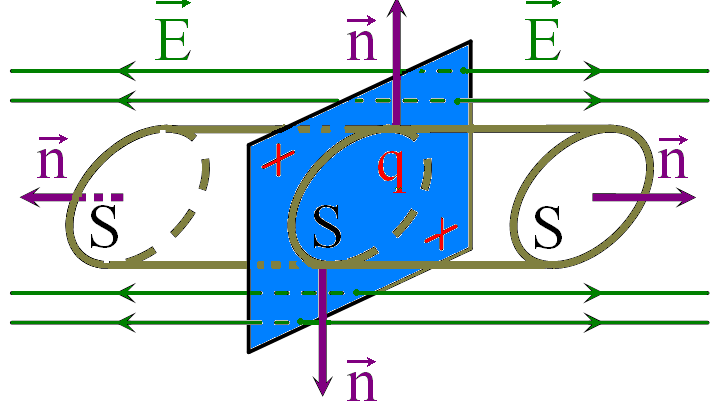
Пусть имеется бесконечная заряженная плоскость, с постоянной поверхностной плотностью заряда σ. |
|
Поверхностная плотность заряда ─ скалярная величина равная отношению модуля заряда, распределённого по какой-либо поверхности к площади этой поверхности, поверхностная плотность численно равна величине заряда, приходящегося на единицу площади поверхности.
|
|
Обозначим на
поверхности плоскости круг площадью S
с зарядом q.
В качестве замкнутой поверхности
мысленно выделим в поле цилиндр с
основанием S,
при этом линии напряжённости поля
плоскости будут перпендикулярны
основаниям цилиндра. Поток вектора
напряжённости через боковую поверхность
цилиндра будет равен нулю, так как угол
,
между
и
,
равен 900 ,
а
.
Тогда полный поток через поверхность
цилиндра равен сумме потоков через его
основания
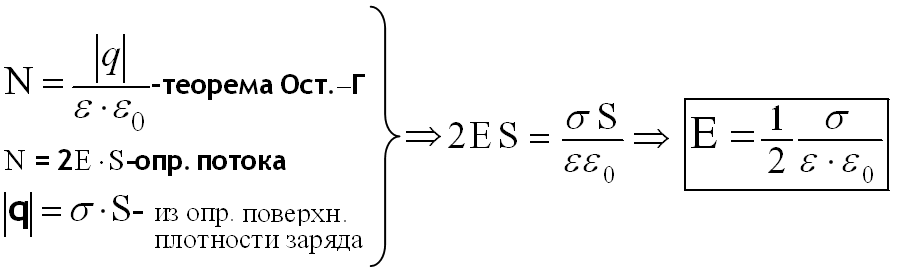
Модуль напряжённости поля двух параллельных разноимённо заряженных плоскостей
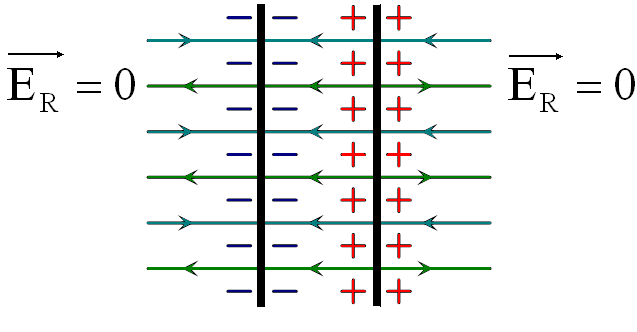
Пусть заряды плоскостей равны по модулю. Тогда, согласно принципу суперпозиции полей, слева и справа от плоскостей их поля вычитаются (линии напряжённости направлены навстречу друг другу), поэтому напряжённость результирующего электрического поля вокруг них будет равна нулю. |
|
|
|
В области между плоскостями поля складываются (линии напряжённости полей обоих плоскостей сонаправлены), поэтому напряжённость результирующего поля между плоскостями будет равна:
|
|
|
|
где q – заряд каждой из плоскостей; S – эффективная площадь поверхности (площадь перекрытия плоскостей); σ ─ поверхностная плотность заряда одной из пластин.
|
|
Линейная плотность заряда ─ скалярная величина, равная отношению модуля заряда, распределённого вдоль какой-либо линии к длине этой линии, линейная плотность заряда численно равна величине заряда, приходящегося на единицу длины линии. |
|
Задание: Используя
теорему Остроградского- Гаусса,
определение потока вектора напряженности
электрического поля и определение
линейной плотности заряда определите
напряженность электрического поля
вокруг бесконечно длинной заряженной
спицы с линейной плотностью заряда
.
Ответ:
