5. Методы решения дискретных задач

Мы убедились, что с помощью булевых переменных можно решать часто встречающиеся задачи оптимизации. Но как решать?

Есть три метода решения задач с булевыми переменными:

• метод ветвей и границ;

• метод сплошного перебора;

• метод фильтрующего ограничения.

Методом ветвей и границ задачи дискретного програм­мирования решаются, как обычные задачи целочисленного программирования. При этом на каждую переменную накладывается два требования:

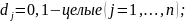
Совершенно очевидно, что выполнение этих двух требо­ваний обеспечивает получение в решении значений [0; 1] т. е. равных 0 или 1.

Пример 4. Требуется решить систему методом сплошного перебора:

max L = 3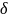 ₁ - 2 ₂ + 5 ₃

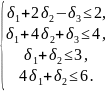
Решение. Так как ₁, ₂, ₃ могут принимать значе­ния 0 или 1 в любом сочетании, рассмотрим все возможные сочетания (табл. 5) в следующей последовательности.

Таблица 5.

№ варианта	1	2	3	(1)	(2)	(3)	(4)	L
1	0	0	0	0	0	0	0	0
2	1	0	0	1	1	1	4	3
3	0	1	0	2	4	1	0	-2
4	0	0	1	-2	1	0	1	5
5	1	0	1	0	2	1	5	8
6	1	1	0	3	5	2	4	1
Требование				<2	<4	<3	<6	max

1. Заполнить все возможные сочетания допустимых зна­чений ₁, ₂, ₃.

2. Определить и записать значения левых частей огра­ничений (1)-(4) и целевой функции.

3. Вычеркнуть те варианты, в которых не удовлетворя­ется хотя бы одно ограничение, как приводящие к недопу­стимым решениям.

4. Из оставшихся вариантов принимается тот, в кото­ром целевая функция максимальна. В примере max L = 8 — в шестом варианте (оптимальном), в котором 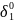= = 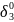1; .

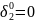Из этого примера видно, что в данном случае всего вариантов будет 2³ = 8 и для каждого варианта надо вычислить четыре ограничения и целевую функцию, т. е. выполнить N = 8(4 + 1) = 40 вычислительных операции. Значит, в общем случае N = 2ⁿ(m + 1), где n — число переменных, m – число ограничений. Следовательно, при увеличении размерности задачи число вычислений резко возрастает (табл. 6).

Таблица 6.

n	ТО
	4	10	15
3	40	88	120
5	160	352	512
10	5120	11264	16384

Для сокращения трудоемкости полного перебора при­меняют различные методы.

Метод фильтрующего ограничения предполагает следую­щую последовательность действий.

1. Принимают некоторые значения ₁, ₂, ₃, например: 1, 0, 0.

2. Определяют значение целевой функции при таком на боре переменных L = 3 ₁ - 2 ₂ + 5 ₃ = 3*1 – 2*0 + 5*0 = 3.

3. Далее устанавливают новые значения переменных и целевой функции; причем если полученная целевая функ­ция меньше 3, то этот вариант не рассматривают. Дли исключения возможного рассмотрения такого варианта, вво­дят дополнительное ограничение 3 ₁ - 2 ₂ + 5 ₃ ≥ 3, кото­рое называют фильтром (Ф).

4. Составляют таблицу (табл. 7), в которой для каж­дого варианта проверяют выполнение всех ограничений, включая Ф.

Если вычисление прекращается и величины не опреде­лены, то в клетках таблицы ставится прочерк.

Введение фильтрующего ограничения Ф привело к сокра­щению числа вычисляемых величин (24 вместо 40, т. е. 60%).

№ варианта	1	2	3	F = Ф	(1)	(2)	(3)	(4)
1	0	0	0	-	-	-	-	-
2	1	0	0	3	1	1	1	4
3	0	1	0	-2	-	-	-	-
4	1	1	0	1	-	-	-	-
5	0	0	1	5	-1	1	0	1
6	1	0	1	8	0	2	1	5
7	0	1	1	3	1	5	-	-
8	1	1	1	6	2	6	-	-
Требование				> 3	< 2	< 4	< 3	< 6

Число вычислений можно уменьшить, если фильтр бу­дет не постоянным для всего цикла вычислений, а изменяю­щимся, т. е. если в ходе вычислений при каком-либо набо­ре переменных значение целевой функции окажется луч­ше, чем у фильтра, то это новое допустимое решение принимают для следующих вычислений в качестве нового фильтра. Такой фильтр называют адаптивным.

Например, из таблицы видно, что в пятом варианте Ф = 5. Поэтому для дальнейших вычислений в качестве фильтрую­щего ограничения принимаем 3 ₁ - 2 ₂ + 5 ₃ ≥ 5 (Ф₁). Од­нако для следующего варианта значение целевой функции будет еще больше (Ф = 8) и в качестве фильтрующего огра­ничения принимается 3 ₁ - 2 ₂ + 5 ₃ ≥ 8 (Ф₂). Для седьмо­го и восьмого вариантов значение целевой функции не удов­летворяет требованиям фильтра Ф₂ и значения ограничений не вычисляем. Значит, трехкратный фильтр (Ф, Ф₁, Ф₂) позволил сократить вычисления еще на 4, т. е. надо выпол­нить 20 вычислений вместо 40 (50%). Более значительное сокращение трудоемкости достигается методом Беллмана с фильтром, где наибольший Ф получают сразу.