Содержание

Обзор литературы 8

Введение

Переход к рыночной экономике и функционированию рыночного механизма регулирования включает в себя совершенствование этапа планирования, который становится тесно связанным с прогнозированием эффективных направлений экономического развития. Актуальными являются разработка математического описания экономических процессов и развитие методов оптимизации для решения возникающих сложных математических задач. Это особенно существенно для определения вариантов экономического развития на перспективу, когда необходимо учитывать крупные и продолжительные народнохозяйственные мероприятия: создание и развитие территориально-производственных комплексов, обеспечение скоординированных программ исследований и разработок, распределение ресурсов для выполнения отдельных комплексов работ при программно-целевом планировании, осуществление выпуска крупных изделий, производство которых требует значительного времени. Традиционный путь решения линейных динамических целочисленных задач состоит во введении дискретного времени, получении в результате этого линейных алгебраических соотношений и применении описанных в литературе общих или специализированных методов целочисленного линейного программирования (ЦЛП).

Оптимальное решение является наилучшим только в рамках использования данной модели. Не следует считать, что это действительно самое лучшее решение анализируемой задачи.

Целью данной работы является обзор и анализ методов решения специальных задач линейного программирования.

Обзор литературы

При написании курсовой работы мною была использована книга «Математические методы и модели для менеджмента» (Глухов В. В., Медников М. Д., Коробко С. Б.), имеющаяся в библиотеке колледжа. Именно в ней наиболее полно изложен материал о специальных задачах линейного программирования. Так же в издании имеется достаточное количество схем и примеров для структурирования прочитанной информации.

Вторым, но не менее важным источником, служит книга «Методы оптимизации» (Харчистов Б.Ф.). В ней изложены основные понятия и теоретические положения курса "Методы оптимизации". Приведены алгоритмы, реализующие различные методы решения оптимизационных задач.

1. Целочисленное программирование

Первые упоминания о линейных уравнениях возникли еще за несколько веков до нашей эры.

В Древней Греции Диофант (II-III вв.) формулирует уравнения, в которых искомые переменные — целые. На­пример, для уравнения первой степени, а₀ + a₁x₁ = 0, где a₀, a₁ — целые, решение x₁ = -a₀/a₁ — целое, если a₀ де­лится на a₁ без остатка, т. е. такое уравнение не всегда разрешимо в целых числах. Из двух уравнений 3x₁ - 27 = 0 и 5x₂ + 21 = 0 только первое имеет целое решение: x₁ = 27/3 = 9, а второе — нет, так как x₂ = -21/5.

Для уравнения с двумя неизвестными: a₁x₁ + a₂x₂ = 0, где a₂, a₁ — целые, решение будет x₁ = -(a₂/a₁)x₂. Например,

10x₂ - 5x₂ = 0 или x₁ = 0,5x₂ . (1)

Из этого примера можно сделать следующие выводы: уравнение имеет бесчисленное множество решений, так как n > m; решение — целое, если x₂ — четное.

Для того чтобы из множества допустимых решений вы­брать одно — оптимальное, необходимо, как нам уже извест­но, добавить к условию (1) целевую функцию. Задачи опти­мизации, в которых решение должно быть в целых числах, называют задачами целочисленного программирования. Если в этой задаче целевая функция и ограничения — линейные зависимости, то ее называют целочисленной задачей линейного программирования; если же хотя бы одна зависимость будет нелинейной, то такая задача формулируется как целочисленная нелинейного программирования.

Большинство практических задач принятия решения сводится к целочисленным задачам линейного программи­рования.

Если к условию (1) добавить такие, например, гранич­ные условия:

2 ≤ x₁ ≤ 8; 1 ≤ x₂ ≤ 3

то можно видеть, что такая система решения не имеет. Отсюда следует, что задача целочисленного программиро­вания не всегда имеет решение, т. е. она не совместна.

Под целочисленным или дискретным программирова­нием понимают такие задачи (обычно линейные), в которых искомые переменные по смыслу могут принимать только целые значения: число рабочих, разделяемых по рабочим местам; количество единиц оборудования, устанавливаемых на заданной площади, и т. п.

Аналитическая задача целочисленного программирова­ния формулируется:

max(min) L =

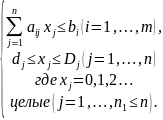
Если n₁ = n, то задачу называют полностью целочис­ленной; если n₁ < n, то — частично целочисленной.

Предположим, что задача имеет многогранник реше­ний (рис. 1). Если наложить требование целочисленности, то допустимое множество решений выразится в си­стему точек и уже не будет выпуклым.

Е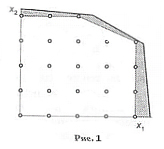 сли добавить новые ограничения, связывающие внеш­ние целочисленные точки, а затем в качестве многогранника использовать все выпуклое множество, ограниченное осями координат и новым контуром, то получим новую задачу линейного программирования со следующими свойствами:

• новый многогранник решений содержит все целые точки, за­ключавшиеся в первоначаль­ном многограннике решений; любая его угловая точка целая;

• так как целевая функция достигает оптимума в угло­вой точке, то построением многогранника обеспечива­ется целочисленность оптимального решения.

Таким образом, решение задач целочисленного программирования трудоемко. Поэтому по возможности лучше не накладывать ограничений целочисленности переменных.

В ряде случаев задачу целочисленного программирования решают следующим образом:

1. как непрерывную задачу линейного программирования;

2. округляют переменные;

3. проверяют допустимость округленного решения;

4. если решение допустимое, то оно принимается как целочисленное.

При необходимости точного решения применяют специ­альные методы, где учитывается, что множество решений лю­бой целочисленной задачи — конечно. Например, в задаче с переменными x₁, x₂: 0 < x₁ ≤ 4; 0 < x_j ≤ 5. Число возможных решений 4*5 = 20. Следовательно, возможен полный пере­бор всех возможных сочетаний целочисленных x₁, x₂ и выбор из них наилучших в смысле целевой функции. Трудоемкость этого метода возрастает с ростом числа переменных и области граничных условий, и для реальных задач он неприменим.

Поэтому в реальных задачах применяют методы, в ко­торых не рассматривают все возможные альтернативы. Рас­пространены методы отсечений и методы возврата, среди которых наиболее известен метод ветвей и границ. Метод отсечений для программной реализации сложен.