
- •Содержание
- •Foreword
- •Вступительное слово
- •Введение
- •1. Основные свойства жидкости
- •2. Одномерное движение несжимаемой жидкости
- •2.1. Основные понятия и уравнения
- •2.2. Истечение жидкости из отверстия
- •2.3. Внезапное расширение и сжатие потока
- •В цилиндрических каналах
- •Значения коэффициентов потерь при различной
- •3. Ламинарное и турбулентное движение потока жидкости
- •3.1. Ламинарное движение жидкости
- •3.2. Турбулентное движение жидкости
- •3.3. Уравнения энергии
- •4. Течение жидкости в трубопроводах
- •4.1. Гидродинамическое подобие
- •Соотношение масштабов подобия при различных законах моделирования
- •4. 2. Расчет трубопроводов
- •4.2.1. Расчет простых трубопроводов
- •4.2.2. Примеры расчетов простых трубопроводов
- •4.2.3. Расчет сложных трубопроводов
- •4.2.3.1.Трубопроводы с параллельными ветвями
- •4.2.3.3. Трубопроводы с непрерывной раздачей
- •Трубопроводы с кольцевыми участками
- •Примеры расчета сложных трубопроводов
- •5. Неустановившееся движение жидкости
- •5.1. Неустановившееся напорное движение жидкости
- •5.2. Гидравлический удар
- •6. Гидравлическое оборудование
- •6.1. Лопастные насосы
- •6.2. Насосная установка и ее характеристика
- •6.3. Вихревые и струйные насосы
- •6.4. Объемные гидромашины
- •6.5. Поршневые насосы
- •6.5.1. Неравномерность подачи поршневых
- •И роторных насосов
- •При кавитации в цилиндре
- •7. Методика эквивалентных структурных преобразований гидродинамических звеньев
- •Определение првпэ простейших соединений
- •И точкой слияния потоков
- •С точками разветвления потоков
- •8. Определение гидродинамической структуры объектов в нестационарных условиях
- •9. Измерительное оборудование
- •9.1. Измерение расхода жидкости в трубопроводе
- •9.1.1. Расходомеры на основе измерения
- •9.1.2. Поплавковый расходомер
- •9.1.3. Магнитно-индуктивные расходомеры
- •Магнито-индуктивного расходомера
- •9.2. Измерение давления жидкостей
- •9.2.1. Манометры с запирающей жидкостью
- •9.2.2. Манометры с подпружиненным датчиком
- •С трубчатой пружиной
- •9.2.3. Манометрические преобразователи
- •И вид манометрического преобразователя
- •9.2.4. Цифровые манометры
- •9.3. Измерение разности давлений
- •9.3.1. Дифференциальные манометры
- •9.3.2. Дифференциальные манометры
- •9.3.3. Дифференциальные манометры
- •С индуктивным съемом сигналов
- •9.4. Измерение уровня наполнения жидкостями
- •Заключение
- •Список литературы
- •Водная инженерия: гидравлические процессы, оборудование и приборы контроля
4. 2. Расчет трубопроводов
На практике используют простые и сложные трубопроводы. Простым считают трубопровод, в котором жидкость транспортируется от питателя к приемнику без промежуточных ответвлений потока.
4.2.1. Расчет простых трубопроводов
Трубопроводы широко используют в гидравлических установках для транспортировки жидкостей, газов, различных смесей и т.п. Различного типа трубопроводы являются неотъемлемыми элементами любой системы подготовки воды и очистки сточных вод.
Исходным уравнением для расчета простого трубопровода является уравнение баланса напоров (уравнение Бернулли) от входного до выходного сечений (рис. 4.1). При установившемся движении жидкости
![]() ,
,
где Σhп - сумма потерь напора жидкости на пути между выбранными сечениями, которая состоит из потерь на трение по длине и потерь в местных сопротивлениях, расположенных на трубопроводе (к ним же относятся потери при входе потока жидкости из питателя в трубопровод и при выходе потока в приемник).
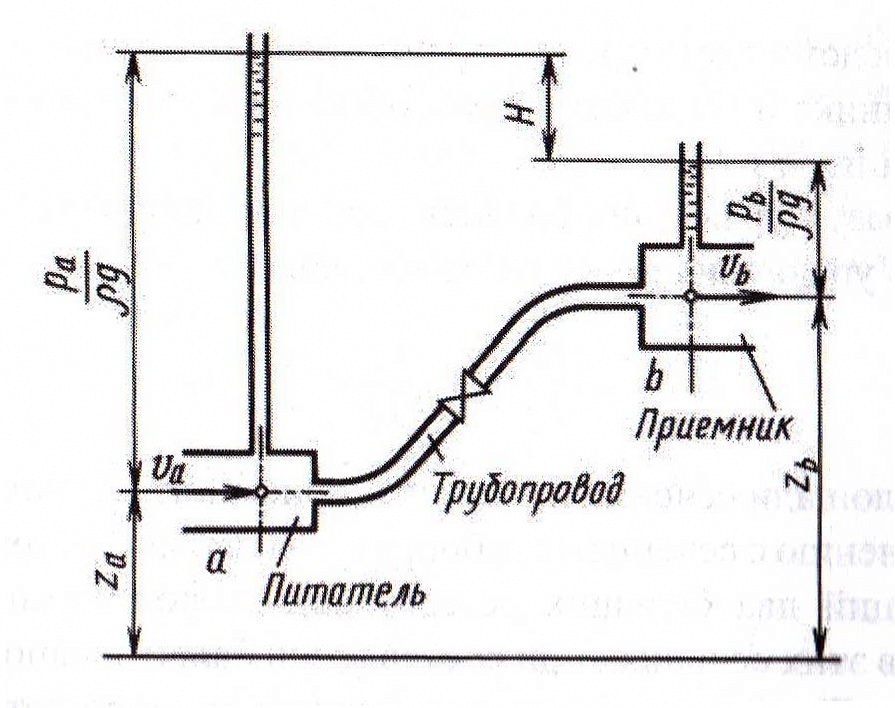

Рис. 4.1. Схема простого трубопровода |
Рис. 4.2. Расчетная схема простого трубопровода |
Для удобства расчетов воспользуемся понятием располагаемого напора трубопровода
![]() ,
,
который представляет собой перепад гидростатических напоров в питателе и приемнике и выражается разностью пьезометрических уровней в сечениях а и b.
Преобразуя уравнение баланса напоров, получим общий вид расчетного уравнения простого трубопровода
![]() (4.10)
(4.10)
Если площади сечений питателя и приемника достаточно велики по сравнению с сечением трубопровода (например, для трубопровода, соединяющего два больших резервуара), то скоростными напорами жидкости в этих сечениях можно пренебречь при составлении баланса напоров. В таком случае расчетное уравнение принимает вид
![]() (4.11)
(4.11)
И оно соответствует процессу, в котором весь располагаемый напор затрачивается на преодоление гидравлических сопротивлений.
Уравнение (4.11) можно также применять независимо от размеров питателя и приемника, когда трубопровод имеет достаточно большую длину, при которой скоростные напоры на входе и выходе из трубопровода оказываются пренебрежимо малыми по сравнению с потерями напора на трение по его длине.
Используем уравнение (4.11) для простого трубопровода, который соединяет два больших резервуара с постоянными уровнями жидкости (рис. 4.2) и трубопровод состоит из k последовательных участков длиной l и диаметром d . При этом показанные на схеме уровни жидкости в резервуарах следует рассматривать в более общем смысле как пьезометрические уровни в питателе и приемнике.
Выразив потери на трение по длине трубопровода и местные потери напора,
![]() ;
;
![]()
получим
![]()
где
λi
и ζi
- коэффициент сопротивления трения и
суммарный коэффициент местных
сопротивлений на каждом участке; Wi
- средняя скорость потока в выходном
сечении трубопровода;
![]() –
потеря напора при выходе из трубопровода
в резервуар, равная скоростному напору
потока в выходном сечении трубопровода
(для турбулентного режима коэффициент
кинетической энергии
–
потеря напора при выходе из трубопровода
в резервуар, равная скоростному напору
потока в выходном сечении трубопровода
(для турбулентного режима коэффициент
кинетической энергии![]() ;
для ламинарного режима в круглой трубе
;
для ламинарного режима в круглой трубе![]() ).
).
Используя уравнение расхода,
![]() ,
(4.12)
,
(4.12)
получим расчетное уравнение простого трубопровода в виде
![]() ,
(4.13)
,
(4.13)
где Sk - площадь выходного сечения трубопровода; Si - площадь сечения участка диаметром d .
Для простого трубопровода длиной l и постоянного диаметра уравнение (4.13) при турбулентном режиме движения жидкости имеет вид
![]() (4.14)
(4.14)
где
![]() – сумма коэффициентов местных
сопротивлений в трубопроводе.
– сумма коэффициентов местных
сопротивлений в трубопроводе.
Выразив скорость движения жидкости через расход и определив числовой множитель при g = 9,81 м/с, получим для круглого трубопровода
![]() (4.15)
(4.15)
В некоторых задачах на определение пропускной способности трубопровода при турбулентном режиме движения целесообразно использовать уравнение (4.14) в виде
![]() ,
,
где
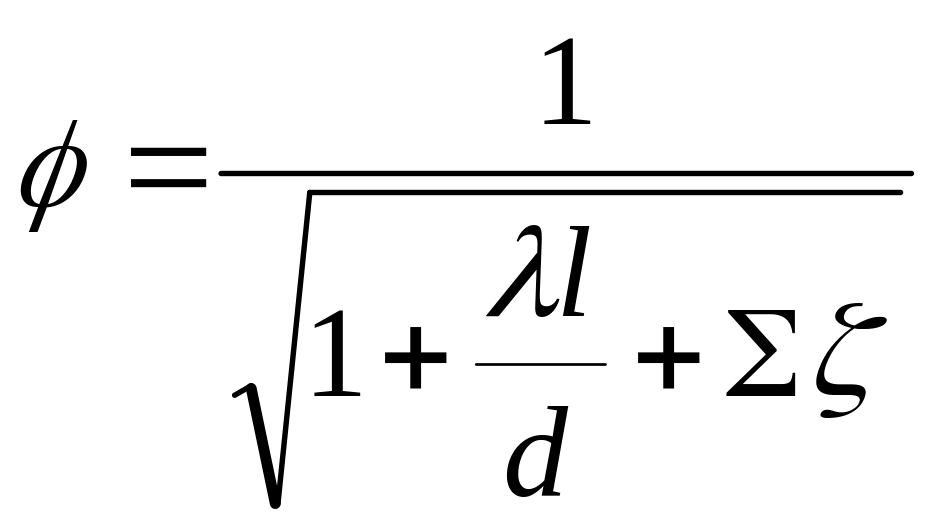 - коэффициент скорости в трубопроводе
- коэффициент скорости в трубопроводе
При этом расход жидкости выразится формулой
![]() ,
(4.16)
,
(4.16)
где![]() –
коэффициент расхода и S
– площадь поперечного сечения
трубопровода.
–
коэффициент расхода и S
– площадь поперечного сечения
трубопровода.
При истечении жидкости из большого резервуара через трубопровод в атмосферу (рис. 4.3) уравнение Бернулли имеет вид
![]() ,
(4.17)
,
(4.17)
где H – располагаемый напор трубопровода, определяемый высотой пьезометрического уровня в резервуаре-питателе над центром выходного сечения трубопровода, – скоростной напор в выходном сечении и Σhп - сумма потерь напора в трубопроводе.

Рис. 4.3. Расчетная схема горизонтального трубопровода
Вследствие того, что потеря напора при выходе потока из трубопровода в данном случае равна нулю, уравнение (4.17) при подстановке в него выражений для определения потерь преобразуется в уравнение (4.13). Следовательно, вышеприведенные расчетные зависимости являются общими для трубопровода при истечении и под уровень и в атмосферу.
Графики напоров, представленные на рис. 4.2 и 4.3, показывают изменение полного напора и его составляющих по длине трубопровода. Линию напора (удельной механической энергии потока) можно построить путем последовательного вычитания потерь, нарастающих по направлению движения потока (заданного пьезометрическим уровнем в питающем резервуаре. Пьезометрическая линия (дающая изменение гидростатического напора потока жидкости) строится путем вычитания скоростного напора из полного напора в каждом сечении.
Пьезометрический
напор![]() в каждом сечении (pи-
избыточное давление) определяется на
графике заглублением центра сечения
под пьезометрической линией, скоростной
напор
в каждом сечении (pи-
избыточное давление) определяется на
графике заглублением центра сечения
под пьезометрической линией, скоростной
напор
![]() –
вертикальным расстоянием между
пьезометрической линией и линией напора.
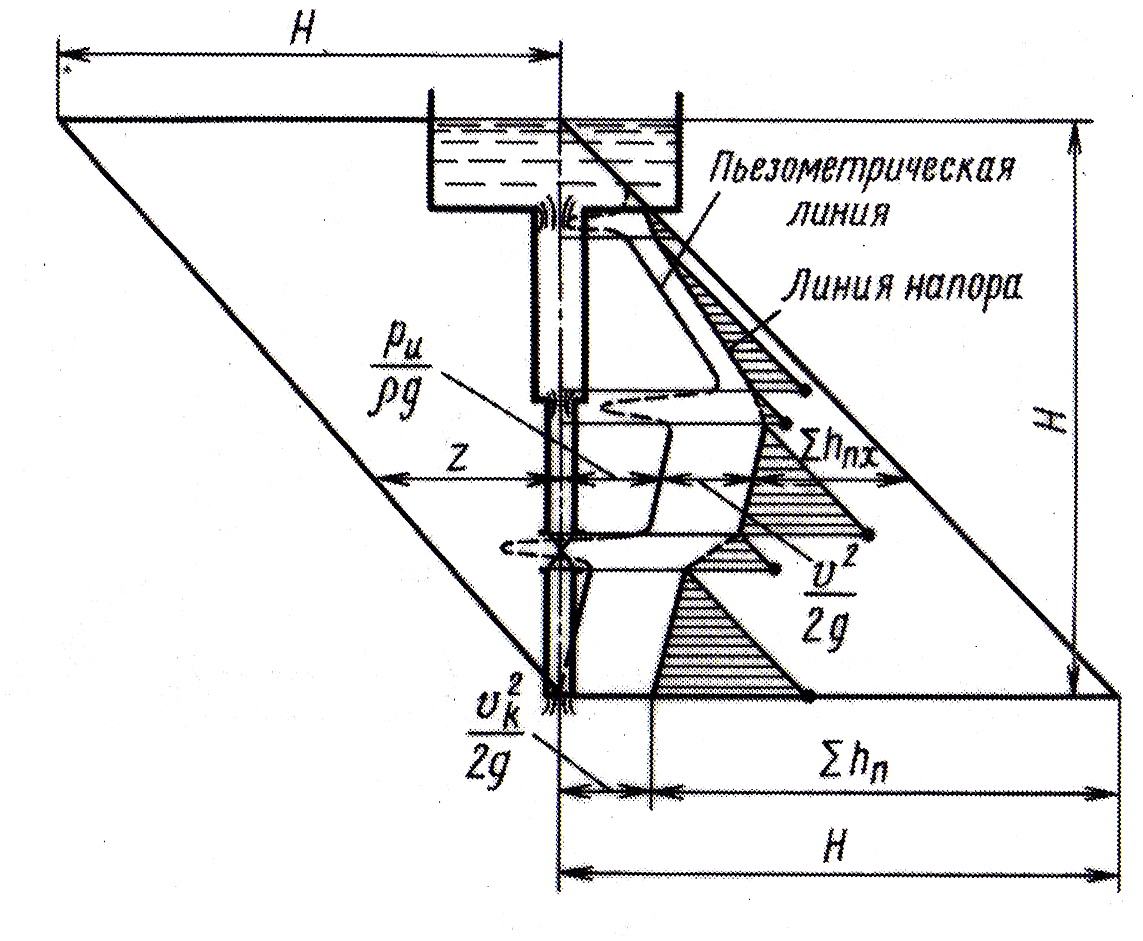
Построение графика напоров для
вертикального трубопровода представлено
на рис. 4.4. Напоры в каждом сечении
откладываются по горизонтали таким
образом, чтобы ось трубы являлась началом
отсчета пьезометрических напоров.
–
вертикальным расстоянием между
пьезометрической линией и линией напора.
Построение графика напоров для
вертикального трубопровода представлено
на рис. 4.4. Напоры в каждом сечении
откладываются по горизонтали таким
образом, чтобы ось трубы являлась началом
отсчета пьезометрических напоров.
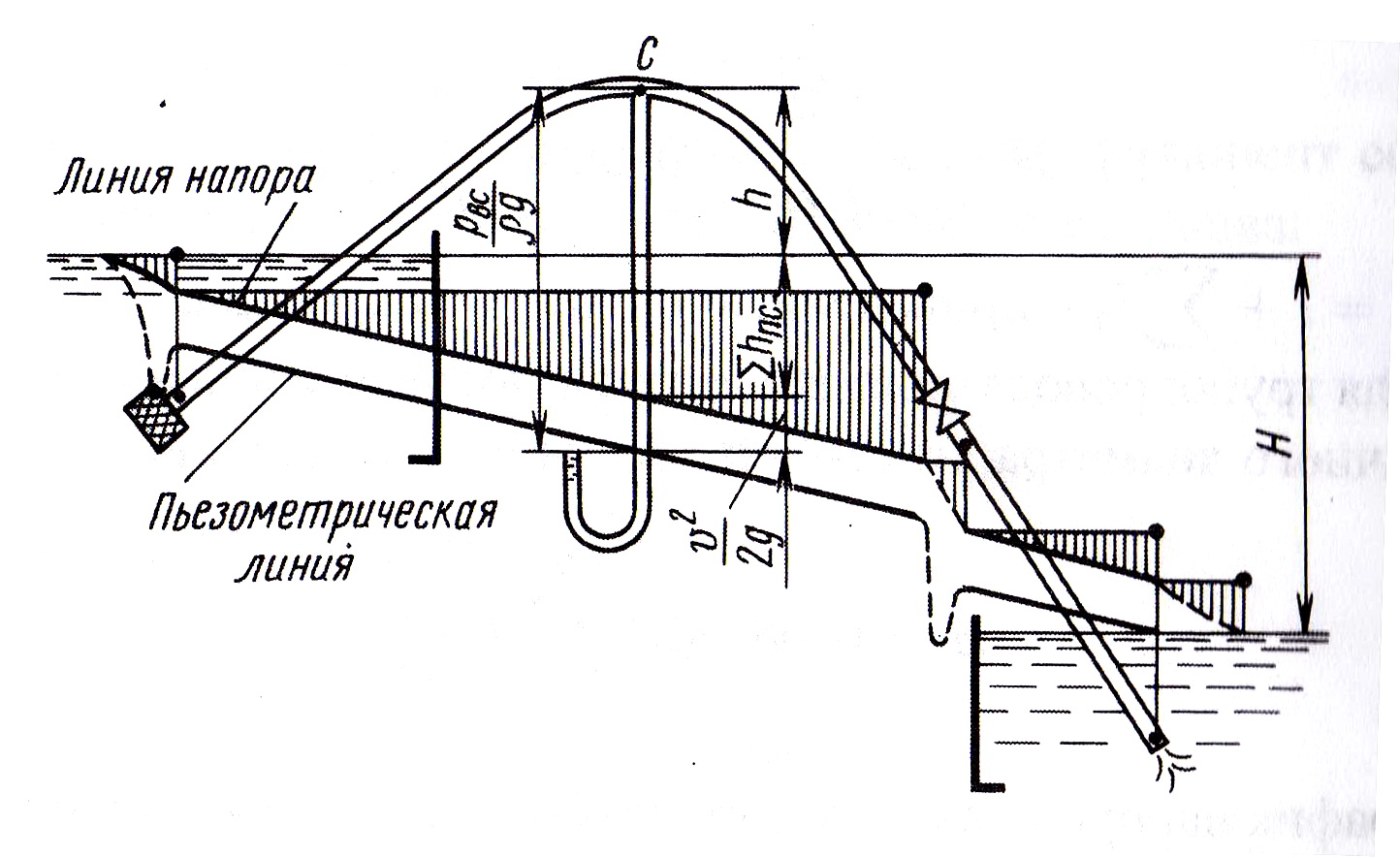
Если часть длины трубопровода находится под вакуумом (например, сифонный трубопровод (рис.4.5), то необходимо оценить значение вакуума в опасном сечении С
![]() ,
(4.18)
,
(4.18)
где h – высота сечения С над начальным пьезометрическим уровнем жидкости в баке-питателе, W – скорость движения жидкости в этом сечении, Σhп.с. - сумма потерь напора на участке трубопровода для этого сечения.
-
Рис. 4.4. Расчетная схема вертикального трубопровода
Рис. 4.5. Схема сифонного трубопровода
Для обеспечения бескавитационной работы трубопровода должно выполняться условие
![]() ,
,
где pат – атмосферное давление, pн.п. - давление насыщенных паров жидкости при данной температуре.
При достаточно большой относительной длине l/d трубопровода скоростной напор W2/2g пренебрежимо мал по сравнению с общей потерей напора в трубопроводе. Поэтому для длинного трубопровода постоянного диаметра расчетное уравнение (4.14) или (4.15) можно заменить приближенным
![]() (4.19)
(4.19)
При расчете длинных трубопроводов, в которых преобладают потери на трение по длине, целесообразно заменить местные сопротивления эквивалентными длинами по формуле (4.20)
![]() (4.20)
(4.20)
При этой замене расчетное уравнение (4.19) можно представить в форме, характерной для трубопровода без местных сопротивлений
![]() ,
(4.21)
,
(4.21)
где
![]() - приведенная длина трубопровода.
- приведенная длина трубопровода.
Для трубопровода, включающего k последовательных участков различного диаметра имеем аналогичное соотношение
![]() (4.22)
(4.22)
График напоров длинного трубопровода строим упрощенно (рис. 4.6), так как относительная малость скоростных напоров позволяет рассматривать линию напора и пьезометрическую линию практически совпадающими.
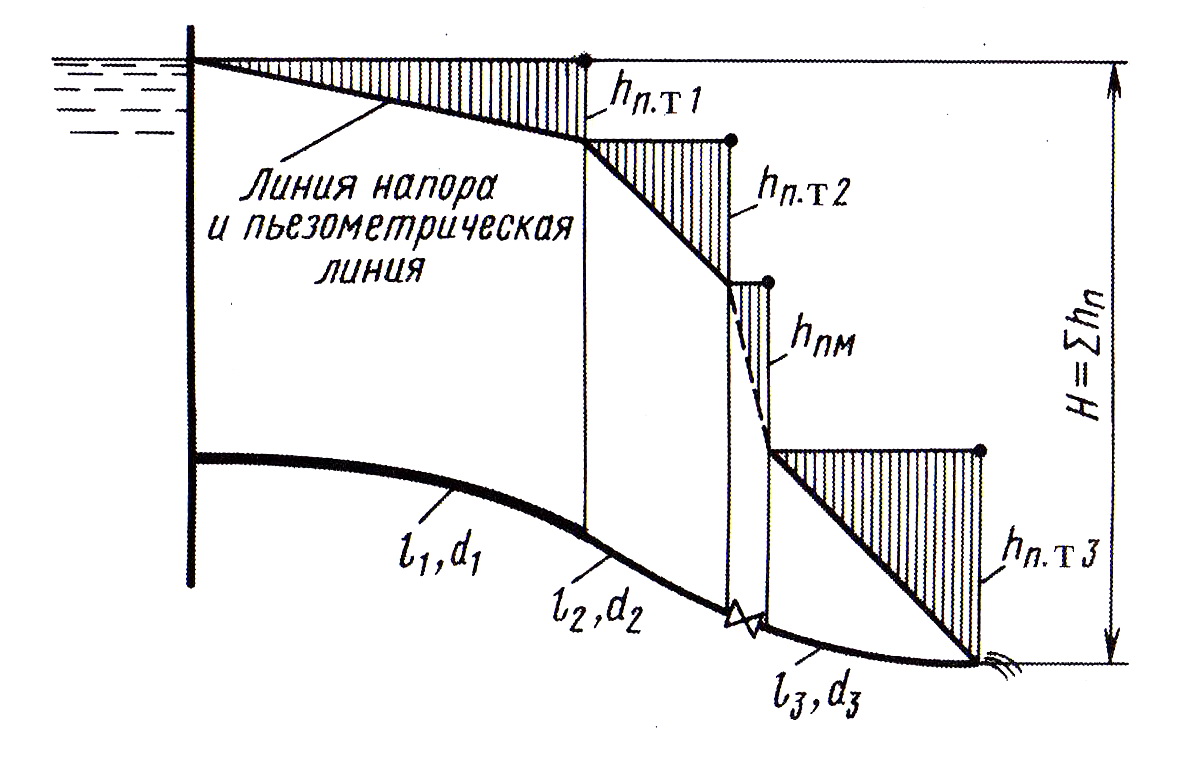
Рис. 4.6. График напоров длинного трубопровода
При расчете трубопровода на основе вышеприведенных соотношений необходимо выбирать коэффициенты местных сопротивлений ζ и коэффициенты сопротивления трения λ. Значения λ при различных режимах движения жидкости определяются следующими зависимостями:
1.Ламинарный режим (Re < 2000) – коэффициент сопротивления трения λ = 64/Re и потеря напора на трения рассчитывается по формуле
![]() (4.23)
(4.23)
2.Турбулентный режим (Re>3000), для которого необходимо рассматривать три варианта:
Область гидравлически гладких труб, для которых коэффициент сопротивления трения определяется по формуле Конакова
![]() (4.24)
(4.24)
или по формуле Блазиуса (Re ≤ 105 )
![]() ,
(4.25)
,
(4.25)
в соответствии с которой потери на трение составляют
![]() .
(4.26)
.
(4.26)
В табл. 4.2. приведены значения коэффициента сопротивления для технически гладких труб (цельнотянутые из меди, латуни, свинца, стекла), а также стальные трубы.
Таблица 4.2.
Значения λ и Re для гидравлически гладких труб
Re |
λ |
Re |
λ |
Re |
λ |
4000 |
0,04 |
40000 |
0,0225 |
400000 |
0,014 |
6000 |
0,036 |
60000 |
0,02 |
600000 |
0,013 |
8000 |
0,0355 |
80000 |
0,019 |
800000 |
0,012 |
10000 |
0,0315 |
100000 |
0,018 |
1000000 |
0,011 |
15000 |
0,0285 |
150000 |
0,0165 |
2000000 |
0,0105 |
20000 |
0,027 |
200000 |
0,0155 |
3000000 |
0,01 |
Переходная область. Можно использовать универсальную формула Альтшулля, которая применима для всех областей турбулентного режима (4.27)
![]() (4.27)
(4.27)
Средние значения эквивалентной шероховатости составляют: для новых стальных цельнотянутых труб 0,1 мм и бывших в употреблении (незначительно корродированных) 0,2 мм. При этом верхняя граница переходной области ориентировочно может быть оценена формулой (4.28)
![]() (4.28)
(4.28)
Область гидравлически шероховатых труб (квадратичная область), в которой значения λ определяются формулой Никурадзе
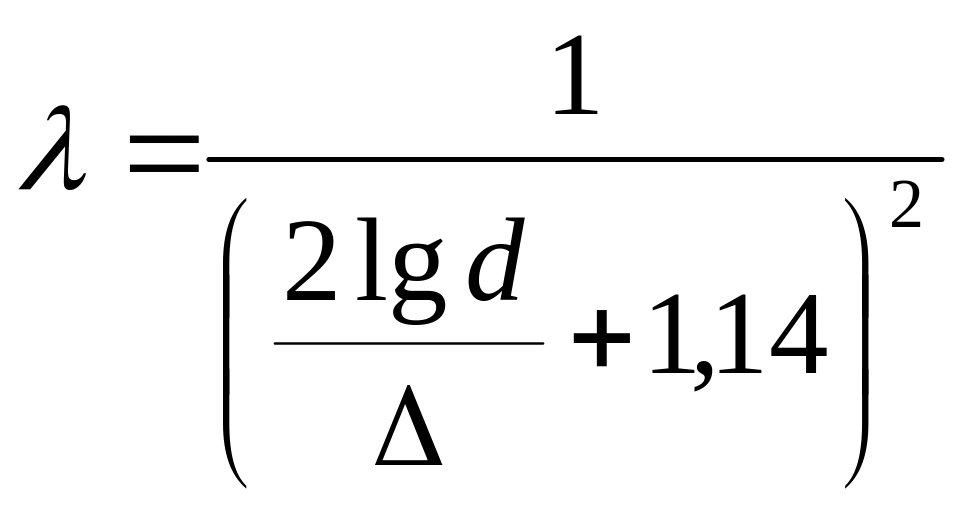 .
(4.29)
.
(4.29)
Или близкой к ней формулой Шифринсона
![]() (4.30)
(4.30)
Для
старых водопроводных (стальных и
чугунных) труб, существенно корродированных
в результате длительной эксплуатации
(![]() мм),
применима также формула
мм),
применима также формула
![]()
Для некруглых труб (прямоугольного, овального и т.п. сечений) потери напора на трение выражаются общей формулой
![]() ,
,
где W – средняя по сечению скорость, Dг - гидравлический диаметр сечения (4F/S), S – периметр трубопровода.
Значения коэффициента сопротивления трению определяются по вышеприведенным формулам, в которых вместо диаметра d используют Dг .
В табл. 4.3. приведены расчетные значения λ в зависимости от отношения d/∆ .
Таблица 4.3
Зависимость λ от d/∆ для квадратичной области
d/∆ |
λ |
d/∆ |
λ |
d/∆ |
λ |
100 |
0,0379 |
1100 |
0,0192 |
2500 |
0,0159 |
200 |
0,0304 |
1200 |
0,0188 |
3000 |
0,0153 |
300 |
0,0269 |
1300 |
0,0184 |
3500 |
0,0148 |
400 |
0,0249 |
1400 |
0,0181 |
4000 |
0,0144 |
500 |
0,0234 |
1500 |
0,0178 |
5000 |
0,0137 |
600 |
0,0223 |
1600 |
0,0176 |
6000 |
0,0132 |
700 |
0,0216 |
1700 |
0,0173 |
7000 |
0,0128 |
800 |
0,0207 |
1800 |
0,0171 |
8000 |
0,0125 |
900 |
0,0202 |
1900 |
0,0169 |
9000 |
0,0122 |
1000 |
0,0197 |
2000 |
0,0167 |
10000 |
0,012 |
На практике используют три основные задачи расчета простого трубопровода. Рассмотрим методику решения каждой из них.
