6 Содержание отчёта

6.1 Сформулировать цель лабораторной работы.

6.2 Привести структурную схему лабораторной установки с подключенными внешними приборами.

6.3 Привести графические зависимости и результаты расчетов, полученные в ходе домашней подготовки.

6.4 Привести таблицы, результаты измерений и графические зависимости, полученные в процессе экспериментальных исследований.

В составе вспомогательных файлов имеется М-функция обработки результатов моделирования LabRabRCS1Obr, к которой можно обратиться либо по нажатию кнопки Graphics, либо переходя в командное окно и выполняя команду

LabRabRCS1Obr(ScopeData2)

которая строит три графика (рисунок 2). По ним легко определить характеристики процесса дискретизации и затем вставить их в черновик отчёта по лабораторной работе.

6.5 Сформулировать выводы по результатам работы.

В выводах необходимо отметить основные экспериментальные результаты, сравнить их с результатами расчетов, сформулировать рекомендации по выбору параметров устройства дискретизации и фильтров, восстанавливающих форму исходного сигнала.

Следует сделать отдельные развёрнутые выводы по каждому пункту эксперимента:

–  по первым двум пунктам – о степени близости каждого из фильтров к идеальному низкочастотному фильтру;

–  по третьему и пятому пунктам – о выборе соотношения между верхней граничной частотой спектра видеоимпульса и частотой дискретизации;

–  по четвёртому пункту – о влиянии начальной фазы несущей частоты при дискретизации и восстановлении радиоимпульса при Различных частотах дискретизации.

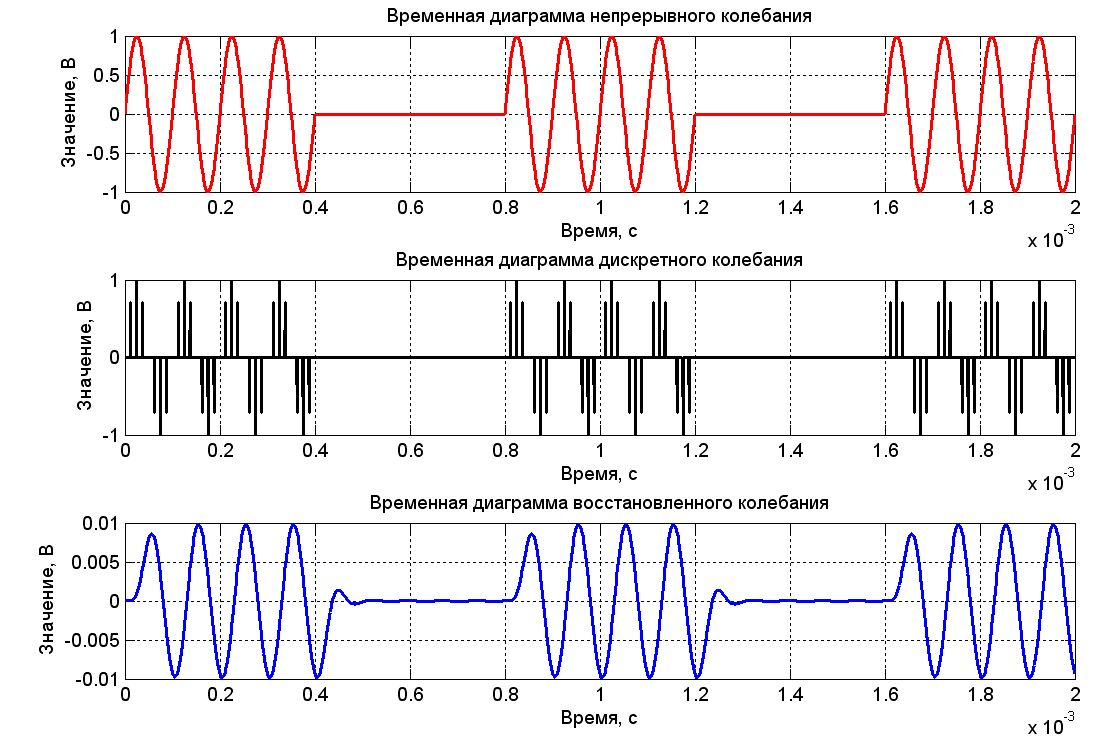
Рисунок 2 – Пример обработки результатов моделирования

7 Контрольные вопросы

7.1. Какова практическая цель дискретизации непрерывных сигналов и сообщений?

7.2. Как оценить верхнюю частоту спектра реального сообщения или сигнала, подлежащую дискретизации?

7.3. Что такое спектр детерминированного сигнала?

7.4. Доказать ортогональность функций отсчетов.

7.5. Указать способы формирования функций отсчетов.

7.6. Сформулировать теорему отсчетов.

7.7. Пояснить с помощью спектральных диаграмм причины возникновения ошибок восстановления непрерывного сигнала при использовании неидеального ФНЧ и дискретизации сигнала с неограниченной полосой частот.

7.8. Определить минимальные значения частоты дискретизации речевого сообщения и телевизионного видеосигнала.

7.9. Определить связь частоты дискретизации экспоненциального сигнала s(t)=1(t)exp(-αt) с погрешностью его представления. Как отражается ограниченность значения F_В на форме экспоненциального сигнала после его восстановления?

Лабораторная работа № 3 модуляцИя гармонического колебания

1 Цель работы

Исследование основных свойств трёх видов модуляции – амплитудной, фазовой и частотной – на примере модуляции гармонического высокочастотного колебания.

2 Теоретические основы анализа модулированных колебаний

Для передачи по радио сигнала с низкочастотными составляющими необходимо переносить спектр сигнала в область высоких частот (частоты более 120 кГц). Для этого в радиопередатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебанием. В общем случае его математическая модель такова, что имеется некоторая совокупность параметра , определяющих форму этого колебания, и некоторые из них зависят от . Физический процесс управления низкочастотным сигналом параметрами несущего колебания называется модуляцией.

В радиотехнике широкое распространение получили системы модуляции, использующие в качестве несущего простое гармоническое колебание

(3.1)

имеющее три свободных параметра U, и . Изменяя во времени один из параметров, можно получать различные виды модуляции.

Если переменной оказывается амплитуда сигнала U(t), причем остальные два параметра и неизменны, то имеется амплитудная модуляция несущего колебания. Форма записи амплитудно-модулированного, или АМ-сигнала, такова:

(3.2)

Здесь U_m – постоянный коэффициент, равный амплитуде не­сущего колебания в отсутствие модуляции; М – коэффициент амплитудной модуляции. Величина М характеризует глубину амплитудной модуляции.

При амплитудной модуляции связь между огибающей U(t) и модулирующим полезным сигналом s(t) принято определять следующим образом:

(3.3)

Однотональная амплитудная модуляция. Простейший АМ-сигнал может быть получен в случае, когда модулирующим низкочастотным сигналом является гармоническое колебание с частотой Ω. Такой сигнал

(3.4)

называется однотональным АМ-сигналом.

Используя известную тригонометрическую формулу произве­дения косинусов, выражение (3.4) можно представить как

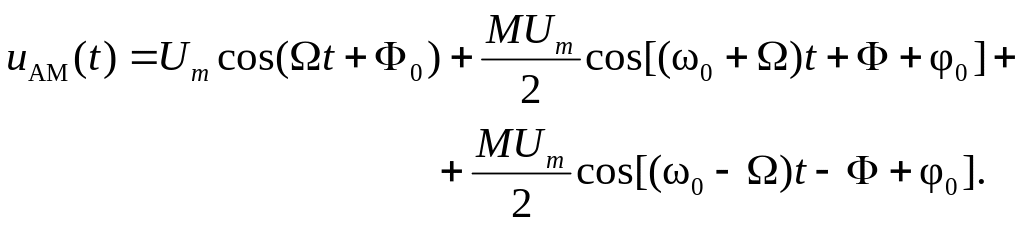(3.5)

Формула (3.5) устанавливает спектральный состав одно­тонального АМ-сигнала, где приняты обозначения:

– несущая частота, – верхняя боковая частота,

– нижняя боковая частота.

Спектр частот, занимаемый АМ-сигналом с однотональной амплитудной модуляцией, согласно формуле (3.5) равен

(3.6)

Чтобы найти среднюю мощность сигнала, величину необходимо усреднить по достаточно большому отрезку времени T: При усреднении все взаимные мощности дадут нулевой результат, поэтому средняя мощность АМ-сигнала окажется равной сумме средних мощностей несущего и боковых колебаний:

(3.7)

откуда следует, что кпд АМ-модуляции

(3.8)

Так, даже при 100 %-ной модуляции (М = 1) доля мощности обоих боковых колебаний составляет всего лишь 50% от мощности немодулированного несущего колебания. Поскольку информация о сообщении заключена в боковых колебаниях, можно отметить неэффективность использования мощности при передаче АМ-сигнала.

Многотональная амплитудная модуляция. Введем совокупность парциальных (частичных) коэффициентов модуляции и запишем аналитическое выражение сложномодулированного (многотонального) АМ-сигнала в форме, которая обобщает выражение (3.4):

(3.9)

Спектральное разложение проводится так же, как и для одно­тонального AM-сигнала:

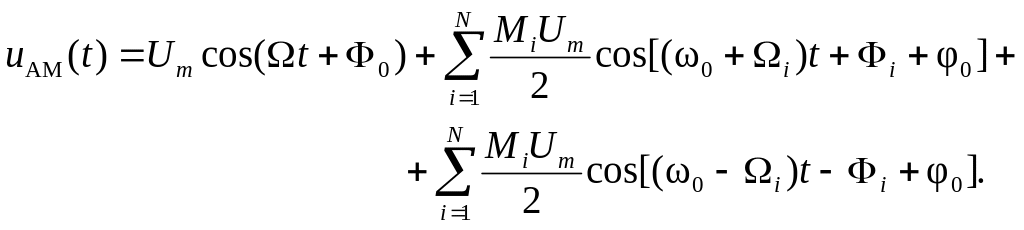(3.10)

Спектр частот, занимаемый АМ-сигналом с многотональной амплитудной модуляцией, также определяется по формуле (3.10):

(3.11)

Средние мощности несущего и боковых колебаний равны

(3.12)

где во всех формулах с (3.9) по (3.12) должно выполняться условие отсутствия перемодуляции

(3.13)

Угловая модуляция. Предположим, что полная фаза связана с сигналом s(t) зависимостью

(3.14)

где – значение частоты в отсутствие полезного сигнала; k некоторый коэффициент пропорциональности. Модуляцию, отвечающую соотношению (3.14), называют фазовой модуляцией (ФМ):

(3.15)

В моменты времени, когда сигнал s(t) достигает экстремальных значений, абсолютный фазовый сдвиг между ФМ-сигналом и смодулированным гармоническим колебанием оказывается наибольшим. Предельное значение этого фазового сдвига называют девиацией фазы . В общем случае, когда сигнал s(t) изменяет знак, принято различать девиацию фазы вверх и девиацию фазы вниз. На векторной диаграмме изображающий вектор постоянной длины будет совершать вращение с непостоянной угловой скоростью. Мгновенная частота сигнала с угловой модуляцией определяется как первая производная от полной фазы по времени:

(3.16)

так что

(3.17)

При частотной модуляции сигнала (ЧМ) между величинами s(t) и имеется связь вида

(3.18)

поэтому

(3.19)

Однотональные сигналы с угловой модуляцией. Анализ ФМ- и ЧМ-сигналов с математической точки зрения гораздо сложнее, чем исследование АМ-колебаний. Поэтому обычно ограничиваются простейшим однотональным сигналам.

В случае однотонального ЧМ-сигнала мгновенная частота где – девиация частоты сигнала. На основании формулы (3.19) полная фаза такого сигнала

(3.20)

где – некоторый постоянный фазовый угол. Отсюда видно, что величина

(3.21)

называемая индексом однотональной угловой модуляции, представляет собой девиацию фазы такого сигнала, выраженную в радианах.

Примем для краткости, что неизменные во времени фазовые углы , и выразим мгновенное значение ЧМ-сигнала в виде

(3.22)

Аналитическая форма записи однотонального ФМ-сигнала будет аналогичной. Однако нужно иметь в виду, что ЧМ- и ФМ-сигналы ведут себя по-разному при изменении частоты модуляции и амплитуды модулирующего сигнала.

Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции. Задачу о представлении сигналов с угловой модуляцией посредством суммы гармонических колебаний несложно решить в случае, когда Для этого преобразуем формулу (3.22) следующим образом:

(3.23)

Поскольку индекс угловой модуляции мал, воспользуемся приближенными равенствами На основании этого из равенства (3.26) получаем

(3.24)

Таким образом, показано, что при в спектре сигнала с угловой модуляцией содержатся несущее колебание и две боковые составляющие (верхняя и нижняя) на частотах и . Индекс т играет здесь такую же роль, как коэффициент амплитудной модуляции М.

Однако можно обнаружить и существенное различие спектров АМ-сигнала и колебания с угловой модуляцией: нижнее боковое колебание имеет дополнительный фазовый сдвиг на 180°.

Спектр сигнала с угловой модуляцией при произвольном значении индекса. Для простейшего случая однотонального ЧМ- или ФМ-сигнала можно найти общее выражение спектра, справедливое при любом значении индекса модуляции m.

Известно, что экспонента с мнимым показателем специального вида, периодическая на отрезке разлагается в комплексный ряд Фурье ( ):

(3.25)

где т – любое вещественное число; – функция Бесселя k-го индекса от аргумента т. После ряда подстановок получим следующую математическую модель ЧМ-или ФМ-сигнала с любым значением индекса модуляции:

(3.26)

При частотной модуляции девиация частоты про­порциональна амплитуде низкочастотного сигнала. В то же время величина не зависит от частоты модулирующего сигнала. В случае фазовой модуляции ее индекс т оказывается пропорциональным амплитуде низкочастотного сигнала независимо от его частоты. Как следствие этого, девиация частоты при фазовой модуляции в соответствии с формулой (3.21) линейно увеличивается с ростом частоты.

Важно отметить, что с ростом индекса модуляции расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами (табл. 3.1) Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией:

(3.27)

Как правило, у реальных ЧМ- и ФМ-сигналов индекс модуляции всегда значительно больше 1, поэтому

(3.28)

Таким образом, сигнал с угловой модуляцией занимает полосу частот, приблизительно равную удвоенной девиации частоты, в то время как для передачи амплитудно-модулированного сигнала требуется полоса частот, равная , т. е. в т раз меньшая.

Таблица 3.1

Амплитуды первых семи гармоник УМ-сигнала

k	m = 1	m = 2	m = 3	m = 4	m = 5
0	0.765	0.224	-0.260	-0.397	-0.178
1	0.440	0.577	0.339	-0.066	-0.328
2	0.115	0.353	0.486	0.364	0.047
3	0.020	0.129	0.309	0.430	0.365
4	0.002	0.034	0.132	0.281	0.391
5	2е-4	0.007	0.043	0.132	0.261
6	2е-5	0.001	0.011	0.049	0.131
7	1е-6	2е-4	0.003	0.015	0.053

Большая широкополосность ЧМ-и ФМ- сигналов обусловливает их применимость для целей радиосвязи лишь на очень высоких частотах, в диапазонах метровых и более коротких волн. Однако именно широкополос­ность приводит к гораздо большей помехоустойчивости сигналов с угловой модуляцией по сравнению с АМ-сигналами.

Следует отметить, что из-за колебательного характера функции Бесселя нулевого индекса при некоторых значениях m* эта функция будет пересекать ось абсцисс, т. е. , что означает: несущее колебание при таких индексах модуляции на частоте в спектре будет отсутствовать. Значения т*, являющиеся корнями данного уравнения, образуют бесконечную возрастающую последовательность чисел (табл. 3.2).

Таблица 3.2

Корни уравнения

Номер корня	1	2	3	4	5	6	7
m*	2.405	5.520	8.654	11.792	14.931	18.071	21.212

Угловая модуляция при негармоническом модулирующем сигнале. Интересная особенность колебаний с угловой модуляцией проявляется в случае, когда модулирующий сигнал не является гармоническим. Рассмотрим для простоты сигнал, промодулированный лишь двумя низкими частотами:

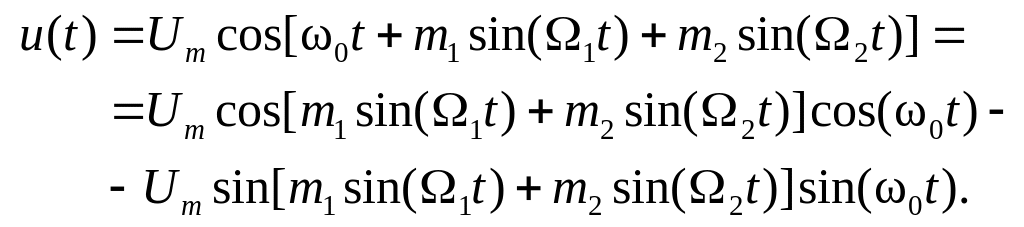(3.29)

Если принять, что парциальные индексы модуляции т₁ и т₂ малы настолько, что можно пользоваться приближенными выражениями для косинуса и синуса: , то выполнив тригонометрические преобразования, можно представить исходный сигнал в виде суммы

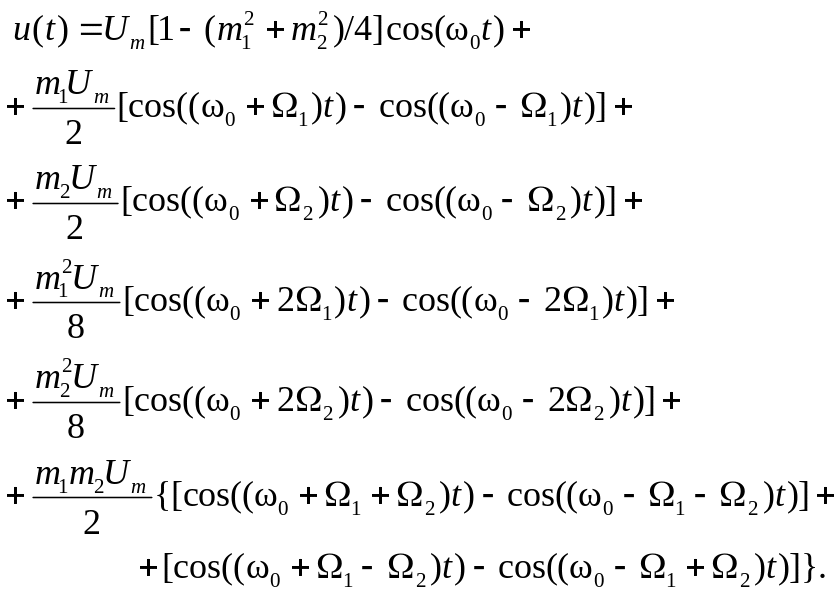(3.30)

Спектральная диаграмма такого двухтонального сигнала изображена на рис. 3.1.

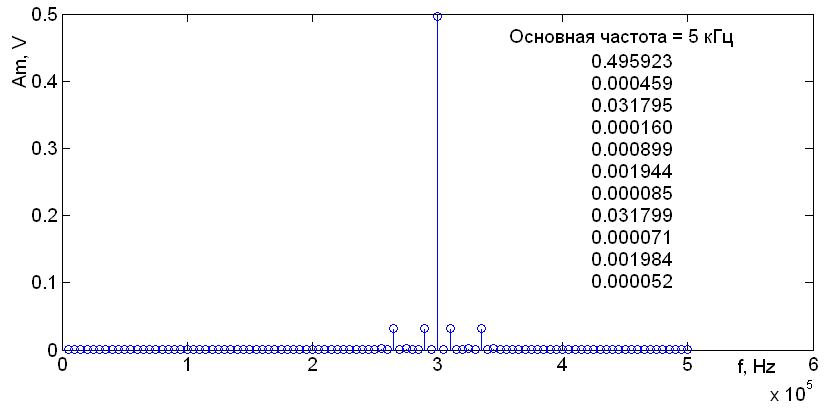
Рисунок 3.1 – Спектральная диаграмма ФМ-сигнала

при m = 0,25, f₁ = 10 кГц, f₂ = 35 кГц, f_нес = 300 кГц

Следует обратить внимание на то, что в спектре рассматриваемого сигнала, помимо частот содержатся ранее отсутствовавшие боковые частоты и Такие частоты в радиотехнике называются комбинационными, а модуляция, при которой они возникают – нелинейной модуляцией.