7. Кривая задана как пересечение двух поверхностей:
а)
б)
в)
Написать уравнения касательной и нормальной плоскости к кривой точке .
Решение.
а) Зададим поверхности неявно:
Касательный вектор к кривой найдем как векторное произведение векторов
и
.
Они перпендикулярны своим поверхностям в любой их точке.
В точке координаты касательного вектора равны
.
Уравнения касательной к кривой в точке в параметрическом виде будут
Уравнение нормальной плоскости запишем в виде
,
где
–
координаты вектора, перпендикулярного
плоскости:
или
.
б) Зададим поверхности неявно:
Аналогично предыдущему, вычисляем
,
,
.
В
точке
координаты касательного вектора равны
.
Он коллинеарен вектору
.
Уравнения касательной к кривой в точке с направляющим вектором запишем в каноническом виде:
.
Уравнение нормальной плоскости к кривой в точке , перпендикулярной вектору , будет
,
или
.
в) Аналогично предыдущему:
,
,
Касательный
вектор коллинеарен вектору
.
Уравнения касательной к кривой в точке с направляющим вектором запишем в каноническом виде:
.
Уравнение нормальной плоскости к кривой в точке , перпендикулярной вектору , будет иметь вид
.
8. Найти векторы канонического репера кривой
в начале координат.
Решение.
Векторы канонического репера – это единичные векторы, направленные по касательной, бинормали и нормали к кривой. Найдем их координаты.
Радиус-вектор
кривой
.
Касательный вектор кривой (вектор
скорости)
.
Вектор ускорения
Дальнейшие вычисления будем проводить
не в общем виде, а в конкретной точке –
начале координат (
).
,
Вектор
,
направленный по бинормали, в точке
имеет координаты
.
Вектор
,
направленный по главной нормали, в точке
имеет
координаты
.
Вычислим координаты единичных векторов, направленных по касательной, главной нормали и бинормали к кривой. Для этого нормируем найденные векторы
,
,
.
Мы нашли векторы канонического репера.
9. Кривая задана параметрическими уравнениями
.
Написать
уравнение касательной прямой, нормальной
плоскости, бинормали, главной нормали,
соприкасающейся и спрямляющей плоскости
в точке
.
Решение.
Уравнения
касательной прямой, бинормали и главной
нормали к кривой в точке
запишем в параметрическом виде
где
–
координаты точки кривой при
,
–
координаты направляющих векторов
соответствующих прямых.
Вычисляем:
Найдем координаты направляющих векторов касательной, главной нормали и бинормали кривой.
Радиус-вектор
кривой
,
.
Вектор
скорости
.
Вектор
ускорения
.
В
точке
имеем
,
.
Вектор бинормали в точке
.
Вектор главной нормали в точке
Параметрическое уравнение касательной к кривой в точке
Уравнение бинормали в точке
Уравнение главной нормали в точке
Уравнения нормальной, соприкасающейся и спрямляющей плоскости к кривой в точке запишем в виде , где – координаты точки кривой при , – координаты векторов, перпендикулярных соответствующим плоскостям. Для нормальной плоскости – это вектор скорости, для соприкасающейся плоскости – это вектор бинормали, для спрямляющей плоскости – это вектор главной нормали.
Уравнением нормальной плоскости к кривой в точке будет уравнение
,
т.е.
.
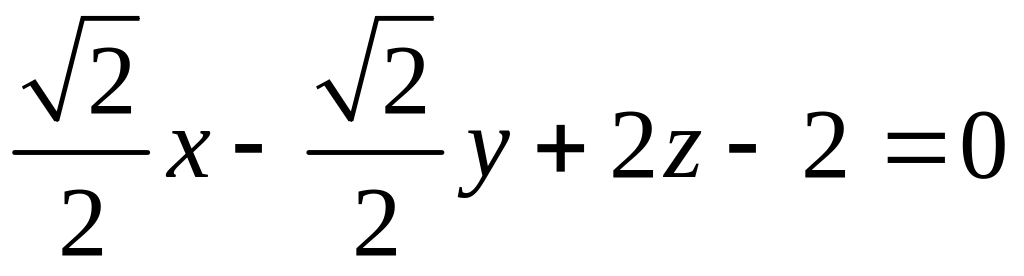Уравнением соприкасающейся плоскости к кривой в точке будет уравнение
,
т.е.
.
Уравнением спрямляющей плоскости к кривой в точке будет уравнение
,
т.е.
