16. Собственные движения евклидовой точечной плоскости.

Произвольное движение f плоскости задается в прямоугольно системе координат ( ) формулами: (1) где (2) есть ортогональная матрица, являющаяся матрицей линейного оператора φ- однородной части движения f в ортонормированном базисе . Т.к определитель ортогональной матрицы равен 1 или -1, то и .

Определение 26.12. Движения плоскости в случае называются собственными, а в случае - несобственными.

Теорема1. Любой ортогональный оператор евкл. пространства имеет в подходящем ортонормир. базисе либо матрицу , либо матрицу , где принадлежит R(жирн.).

в любой прямоугольной системе координат собственное движение может быть задано формулами: (3)

Рассмотрим два частных случая формул (3).

1. В случае, когда , . (4)

При движении, заданном формулами (4), все точки плоскости перемещаются по параллельным прямым, имеющим направляющий вектор а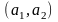 . Величина смещения у всех точек одинакова и равна длине вектора а.Как известно, такое движение называется параллельным переносом плоскости на вектор а.

В случае, когда , имеем:

При этом движении точка О(0, 0) остается неподвижной. Рассмотрим произвольную точку и ее радиус-вектор . Координаты точки М`- образа точки М при движении (5) – так же, как и координаты ее радиус-вектора , задаются формулами (5). Видно, что угол между векторами и равен . Значит каждый отрезок ОМ поворачивается вокруг точки О на угол .

Таким образом, при движении (5) каждый отрезок ОМ поворачивается вокруг точки О на угол . Как известно, такое движение называется поворотом плоскости вокруг точки О на угол .

Теорема. Всякое собственное движение плоскости , заданное формулами (3) при , есть поворот вокруг некоторой точки О`.

Теорема 26.6. Собственные движения плоскости исчерпываются поворотами вокруг любой точки и параллельными сдвигами.

17. Движения трехмерного евклидова точечного пространства.

18. Несобственные движения евклидовой точечной плоскости. Аффинные преобразования евклидова точечного пространства.

19. Пространство An (I). Определение квадрики. Преобразование уравнения квадрики.

Пусть A_n(ℂ) - n-мерное комплексное аффинное пространство, связанное с комплексным векторным пространством (ℂ).

Определение. Пространство A_n(ℂ), в котором фикси­рован репер , а следовательно, и действительное аффинное про­странство A_n, обозначают A_n(i). Точки пространства A_n(i) называются действительными, если они принадлежат пространству A_n, и мнимыми в противном случае. Векторы пространства (ℂ) называются действительными, если они принадлежат пространству , и мнимыми в противном случае.

Пусть в пространстве A_n(i) выбран некоторый репер и задано уравнение (2), где , , - действительные числа, причем среди чисел есть отличные от нуля и = .

Определение 19.2. Квадрикой в пространстве A_n(i) назы­вается множество всех точек этого пространства, координаты ко­торых в репере (1) удовлетворяют уравнению вида (2). Уравнение (2) называется уравнением той квадрики, которую оно определяет.

Пространство A₂(i) называется плоскостью, а квадрики на этой плоскости - линиями второго порядка. Квадрики пространства A₃(i) называются поверхностями второго порядка.

Теорема 2.1. Для того чтобы два уравнения: +2 =0, +2 =0

задавали в выбранном репере одну и ту же квадрику, необходимо и достаточно, чтобы коэффициенты этих уравнений были пропор­циональны, т. е. выполнялись равенства (9).

►Достаточность указанного условия отмечалась выше, необхо­димость следует из леммы 2.3. ◄

Выясним теперь, как преобразуется уравнение квадрики при переходе к новым координатам. Введем следующие обозначения: A=[ а ], A = [а , а₂ ... а_п], S =[ а ],

X= , X′= , A = X = ,

Тогда уравнение квадрики (2) можно записать в виде Х АХ + 2А₁Х + а = 0, (16)

а формулы преобразования координат при переходе от репера (1) к реперу

(О', е′ , е′₂, ... , е′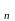 ) (17) в виде Х = SХ' + A₂ (18) (здесь х , х₂, ..., х_п — координаты произвольной точки M Aⁿ(i) относительно репера (1), а x′ , x′₂, ... , x′ — координаты той же точки относительно репера (17)). Подставляя выражение X из равенства (18) в левую часть уравнения (16), получаем Х^ТАХ + 2А₁Х + а = Х'^ТВХ + 2В₁Х' + b, (19) где В = S^TAS; В₁= A^T₂AS + A₁S; b = А^Т₂АА₂ + 2А₁А₂ + а. Здесь мы воспользовались равенствами: А^T = А, X'^TS^TAA₂ = (X'^TS^TAA₂)^T = A^T₂ASX'.

Из равенства (19) следует, что уравнение квадрики (2) отно­сительно репера (17) имеет вид Х'^ТВХ' + 2В₁Х' + b = 0. (20)

Заметим, что при переходе от уравнения (2) к уравнению (20), соответствующему преобразованию координат (18), квадратичная форма Х^ТАХ преобразуется в квадратичную форму X' ВХ', так же как и в результате преобразования X = SX'.

Если рассматривать (18) как формулы аффинного преобразо­вания пространства A (i), мы получим следующую теорему.

Теорема 2.2. При аффинном преобразовании пространства А^п(i) любая квадрика преобразуется в квадрику.