
- •Аффинное пространство и его простейшие свойства. Примеры.
- •Координаты в аффинном пространстве.
- •Плоскости в аффинном пространстве.
- •Аффинно-независимые точки аффинного пространства.
- •Векторное параметрическое уравнение плоскости. Плоскости и системы линейных уравнений.
- •Пересечение и сумма плоскостей аффинного пространства.
- •Аффинное отображение.
- •Изоморфизм аффинных пространств
- •Аффинные преобразования. Выражение аффинного преобразования в координатах.
- •Параллельный сдвиг аффинного пространства. Формулы параллельного сдвига. Центроаффинное отображение. Формулы центроаффинного отображения.
- •Фигуры в аффинном пространстве. Простое отношение трех точек. Отрезок. Середина отрезка. Центр фигуры.
- •Евклидово точечное пространство. Прямоугольная система координат.
- •Плоскости евклидова точечного пространства.
- •Гиперплоскость евклидова точечного пространства. Расстояние от точки до гиперплоскости. Объем параллелепипеда.
- •Движения евклидова точечного пространства. Группа движений евклидова точечного пространства. Метрически эквивалентные фигуры евклидова точечного пространства.
- •Собственные движения евклидовой точечной плоскости.
- •Движения трехмерного евклидова точечного пространства.
- •Несобственные движения евклидовой точечной плоскости. Аффинные преобразования евклидова точечного пространства.
- •Пространство An (I). Определение квадрики. Преобразование уравнения квадрики.
- •Пересечение квадрики с прямой.
- •Асимптотические направления. Центр квадрики.
- •Линии эллиптического, гиперболического и параболического типов. Центры линий второго порядка.
- •Диаметральные плоскости. Диаметры линий второго порядка.
Изоморфизм аффинных пространств
Важным частным случаем аффинного отображения является изоморфизм аффинных пространств.
Определение 12. Биективное аффинное отображение называется изоморфизмом аффинного пространства на аффинное пространство . Если существует изоморфизм , то говорят, что аффинное пространство изоморфно аффинному пространству .
Обозначается
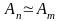 .
.
Теорема 25.11. (Критерий изоморфизма афин. пространств)Аффинное отображение (1) является изоморфизмом аффинных пространств и тогда и только тогда, когда его однородная часть (2) есть изоморфизм линейных пространств Vⁿ и Vm .
Док-во:
По
определению линейное отображение
является изоморфизмом линейных
пространств, когда это отображение –
биекция. Возьмем некоторую точку О
.
Согластно следствию 3 из 25.1, отображения
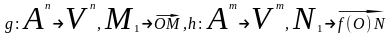 являются биекциями.
являются биекциями.
Пусть
– изоморфизм линейных пространств,
т.е. биекция. Тогда отображение f=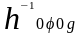 на основании теоремы 3.2 является
биекцией и, следовательно, изоморфизмом
линейных пространств.
на основании теоремы 3.2 является
биекцией и, следовательно, изоморфизмом
линейных пространств.
Обратно,
пусть f
– изоморфизм аффинных пространств,
т.е. биекция. Тогда отображение
 есть
биекция и, следовательно, является
изоморфизмом линейных пространств.
есть
биекция и, следовательно, является
изоморфизмом линейных пространств.
Следствие:
Аффинные
пространства
и
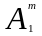 , связанные с линейными пространствами
и
над одним и тем же полем Р, изоморфны
тогда и только тогда, когда n=m
.
, связанные с линейными пространствами
и
над одним и тем же полем Р, изоморфны
тогда и только тогда, когда n=m
.
Аффинные преобразования. Выражение аффинного преобразования в координатах.
Пусть – аффинное пространство, связанное векторным пространством над полем Р.
Определение 13. Изоморфизм f аффинного пространства на себя называется аффинным преобразованием или автоморфизмом этого пространства.
Теорема
13.
При
аффинном преобразовании f
пространства
всякий репер
 (1) переходит в репер
(1) переходит в репер
 (2), а любая точка
(2), а любая точка
 ,
имеющая в репере (1) координаты
,
имеющая в репере (1) координаты
 ,
переходит в точку
,
переходит в точку
 ,
имеющую в репере (2) те же координаты.
,
имеющую в репере (2) те же координаты.
Док-во:
Так как однородная часть
аффинного преобразования является
автоморфизмом линейного пространства
 , то по свойству 5 из 19.4
, то по свойству 5 из 19.4
 базис переходит в базис
базис переходит в базис
 и, следовательно, репер (1) переходит
в репер (2), где
и, следовательно, репер (1) переходит
в репер (2), где
 . Координаты точки М в репере (1)
определяются как коэффициенты в
разложении
. Координаты точки М в репере (1)
определяются как коэффициенты в
разложении
 .
.
Но
при автоморфизме линейного пространства
линейные зависимости между векторами
сохраняются (см. 19.1). Поэтому

т.е.
числа
 являются координатами точки в репере
(2).
являются координатами точки в репере
(2).
Для любых двух реперов (1) и (2) аффинного пространства существует единственное аффинное преобразование пространства , переводящее репер (1) в репер (2).
Теорема 25.15. Для любых двух систем аффинно независимых точек
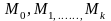 (3)
(3)
 (4)
(4)
пространства существует аффинное преобразование, переводящее точки первой системы в соответствующие точки второй системы.
Пусть
f
произвольное аффинное преобразование
пространства
, переводящее репер (5) в репер (6). Это
преобразование переводит точки (3) в
точки (4). Найдем выражение произвольного
аффинного преобразования f
пространства
в координатах. Фиксируем в пространстве
некоторый репер (1). Рассмотрим репер
(2), полученный из репера (1) с помощью
преобразования f.
Пусть
 – координаты точки
– координаты точки
 в репере (1) и А=
-матрица перехода от базиса
в репере (1) и А=
-матрица перехода от базиса
 (7) пространства
(7) пространства
 к
базису
к
базису
 (8)
(8)
этого
пространства. Возьмем произвольную
точку М и ее образ
 =f
(M)при
отображении f.
Пусть заданы координаты
=f
(M)при
отображении f.
Пусть заданы координаты
 (9) точки М в репере (1) и координаты
(9) точки М в репере (1) и координаты
 (10) точки
в этом же репере. Согласно теореме 25.13.
точка
имеет в репере (2) координаты (9). Как
известно из § 25.2, координаты (10) точки
в репере (1) выражаются через координаты
(9) этой же точки в репере (2) по формулам:
(10) точки
в этом же репере. Согласно теореме 25.13.
точка
имеет в репере (2) координаты (9). Как
известно из § 25.2, координаты (10) точки
в репере (1) выражаются через координаты
(9) этой же точки в репере (2) по формулам:
 .
(11)
.
(11)
Использовав обозначения (8) из §25.2, перепишем формулы (11) в матричном виде:
 (12)
(12)
Формулы
(11) и (12) называются выражением аффинного
преобразования f
в координатах. Матрица А=
называется матрицей аффинного
преобразования f
в репере (1). Отметим, что она совпадает
с матрицей автоморфизма
линейного пространства
в базисе (7), являющегося однородной
частью преобразования f
. Отсюда следует, что |А| (13)
(13)
Покажем, что любые формулы вида (11) или (12) с условием (13) задают аффинное преобразование пространства .
Теорема
25.16. Пусть
А=
-
произвольная, невырожденная матрица с
элементами из поля Р и
 -
произвольный набор чисел из Р. Поставив
в соответствие произвольной точке М с
координатами (9) в репере (1) точку
-
произвольный набор чисел из Р. Поставив
в соответствие произвольной точке М с
координатами (9) в репере (1) точку
 с координатами (10) в том же репере,
вычисленными по формуле (11) или (12),
получим аффинное преобразование f
пространства
.
с координатами (10) в том же репере,
вычисленными по формуле (11) или (12),
получим аффинное преобразование f
пространства
.
Теорема 25.17. Множество всех аффинных преобразований пространства является мультипликативной группой.
