5. Векторное параметрическое уравнение плоскости. Плоскости и системы линейных уравнений.

Зафиксируем в пространстве Aⁿ некоторую точку О. Тогда произвольную точку М пространства Aⁿ можно задать с помощью ее радиуса-вектора r = .

Пусть в пространстве Aⁿ задана плоскость П^k, проходящая через точку М₀ с радиусом-вектором r₀ = и направляющим пространством V ^k. Возьмем в линейном пространстве V ^kкакой-либо базис а₁, а₂,…,а_k. Тогда r = r₀+t₁a₁+ t₂a₂+ …+t_ka_k. (3)

где t₁, t₂, …t_k принадлежит основному полю Р. Когда эти числа принимают всевозможные значения из поля Р, точка М с радиусом-вектором (3) описывает плоскость П^k. Уравнение (3) называется векторным параметрическим уравнением плоскости П^k, а числа t₁, t₂, …t_k – параметрами. Заметим, что уравнения (1) и (2) являются частными случаями уравнения (3).

Если точка О принадлежит плоскости П^k, то, взяв ее в качестве начальной точки , уравнение этой плоскости можно записать в виде r = t₁a₁+ t₂a₂ +…+ t_ka_k.

В этом случае множество всех радиус-векторов точек плоскости П^k совпадает с направляющим пространством V ^k этой плоскости.

Пусть задана система линейных уравнений a_i1x₁+ a_i2x₂+… a_inx_n=b_i , i=1, 2, …, m, (1)

где a_ij ,b_i - числа из поля Р. В параграфе 18.3 систему линейных однородных уравнений с теми же коэффициентами a_ija_i1x₁+ a_i2x₂+… a_inx_n=0 , i=1, 2, …, m, (2)

мы назвали приведенной для системы (1) и (2). Дадим ей геометрическое истолкование. В аффинном пространстве Aⁿ , связанном с линейным пространством V^п над полем Р , зафиксируем некоторый репер (О, е₁, е₂, …,е_п). (3)

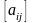Тогда произвольный вектор с V^п может быть задан своими координатами , , …, в базисе е₁, е₂, …,е_п. Будем называть вектор с решением системы (1) (или(2)), если его координаты образуют решение этой системы. Как показано в параграфе 18.2, множество всех векторов, являющихся решениями системы (2), есть (n - r)-мерное подпространство V ^{n – r} линейного пространства V ⁿ , где r – ранг матрицы . Если а₁, а₂, …, а _{n – r} - базис этого подпространства, то каждый вектор r V ^{n – r} можно представит в виде r = t₁a₁+ t₂a₂ +…+ t _{n – r}+ a _{n – r} , t_i P. (4)

Если система (1) совместна и r₀ – одно из решений этой системы , то, согласно теореме 18.3, все ее решения задаются формулой r = r₀+ t₁a₁+ …+ t _{n – r}+ a _{n – r} , t_i P. (5)

Точка М Aⁿ называется решением системы (1) (или(2)), если ее радиус-вектор r = является решением этой системы. Так как уравнение (5) задает (n - r)-мерную плоскость, направляющее пространство которой есть пространство решений системы (2), то справедлива.

Теорема 25.5. Пусть (1) – совместная система линейных уравнений, r-ранг ее матрицы. Множество точек аффинного пространства Aⁿ, являющихся решениями этой системы, есть (n - r)-мерная плоскость, направляющее пространство которой совпадает с пространством решений приведенной системы (2).

Заметим, что плоскость, заданная системой линейных уравнений, проходит через начало координат тогда, когда эта система однородная. Верна и обратная

Теорема 25.6. Пусть в аффинном пространстве Aⁿ фиксирован репер (3). Тогда любая плоскость П^k пространства Aⁿ есть множество всех решений некоторой линейной системы.

Следствие: Линейное уравнение a₁x₁+ a₂x₂+…+ a_nx_n= b (7)

задает в пространстве Aⁿ гиперплоскость, и обратно, любая гиперплоскость в Aⁿ может быть задана уравнением (7)