20. Пересечение квадрики с прямой.

Выберем в пространстве Aⁿ(i) некоторый репер и рассмотрим квадрику, определяемую в этом репере уравнением +2 =0. (1) Найдем точки пересечения квадрики (1) с прямой x = b +c t, i =1, 2, ... , п, (2)

где b , c — действительные числа. Подставляя выражения x из формул (2) в уравнение (1) и приводя подобные члены, получаем уравнение относительно t:( )t +2pt+q=0, (3) где p = +2 ; q = +2 .

Подставляя корни уравнения (3) в качестве значений t в форму­лы (2), получаем координаты всех искомых точек пересечения. Рассмотрим следующие два случая:

1) ≠ 0; 2) = 0.

В первом случае уравнение (3) — квадратное, и в зависимости от. значений его корней t₁ и t₂ имеются три возможности:

а) t₁, t₂ действительны и различны, прямая (2) пересекает квад­рику (1) в двух различных действительных точках;

б) t₁ = t₂ — действительное число, прямая (2) имеет с квадри­кой (1) одну общую действительную точку;

в) t₁ и t₂ не действительны, прямая (2) не пересекает квадрику

(1) в действительных точках, но имеет с ней две общие мнимые точки.

Во втором случае имеем:

г) р ≠ 0, уравнение (3) — линейное, и прямая (2) имеет с квадрикой (1) одну общую действительную точку;

д) р = 0, q ≠ 0, равенство (3) не выполняется, прямая (2) не имеет с квадрикой (1) общих точек;

Рис. 3.1 е) p = 0, q = 0, равенство (3) явля­ется тождеством, все точки прямой (2) принадлежат квадрике, т. е. сама прямая принадлежит квадрике.

На рис. 3.1 изображена гипербола и пять прямых различных типов.

21. Асимптотические направления. Центр квадрики.

Выберем в пространстве Aⁿ(i) репер (О, е , е₂, ... , е ) (1)и рассмотрим квадрику +2 =0. (2)

Пусть задан ненулевой вектор с (с₁ ,с₂, ..., с_n), (3) действительный или мнимый. Будем говорить, что все векторы с, где — произвольное, отличное от нуля комплексное число, задают в пространстве Vⁿ(i) одно определенное направление, любой же другой ненулевой вектор задает другое направление.

Направление, определяемое вектором (3), будем называть дейст­вительным, если существует такое число а, что все координаты вектора ас действительны, в противном случае — мнимым.

Определение 4.1. Hаправление вектора (3) называется асимптотическим относительно квадрикu (2), если =0. (4)

Поскольку левая часть уравнения квадрики (2) в репере (1) определена с точностью до числового множителя, отличного от нуля, определение асимптотического направления не зависит от выбора уравнения заданной квадрики в фиксированном репере. Кроме того, имеет место

Теорема 4.1. Асимптотическое направление относительно квад­рики (2) не зависит от выбора репера.

► Запишем уравнение квадрики (2) в виде Х^ТАХ + 2А₁Х + а = 0, (5)

а равенство (4), определяющее асимптотическое направление, в виде С^TАС = 0, (6)

где С^T = [с₁ ,с₂, ..., с_n].

Пусть переход к новому реперу задается формулами: X = SX' + A₂, (7) C = SC′, (8)

где X' — столбец новых координат точки М; C′ — столбец новых координат вектора (3). В новом репере уравнение квадрики (5) имеет вид X^′TS^TASX' + B_lX' + b = 0. (9) Используя формулу (8), получаем C^TAC = C'^TS^TASC.

Но отсюда следует, что равенство (6) равносильно равенству C'^TS^TASC' = 0,

определяющему асимптотическое направление относительно квад­рики (9). ◄

Проведенному сейчас рассуждению можно дать и другое истол­кование, а именно: будем рассматривать равенства (7) как формулы аффинного преобразования пространства Aⁿ(i), выражающие коорди­наты точки М(x , x₂,...,x ) (прообраза) в репере (1) через координаты точки М'(x′ , x′₂, ... , x′ ) (образа) в том же репере. При этом преобразовании квадрика (5) перейдет в квадрику (9), а вектор (3) —в вектор с′ (с′₁ ,с′₂, ..., с′_n). Тогда очевидно, что имеет место следующая

Теорема 4.2. Пусть вектор с имеет асимптотическое (неасимп­тотическое) направление относительно квадрики К и f — аффинное преобразование пространства Aⁿ(i) с однородной частью . Тогда вектор (с) имеет асимптотическое (неасимптотическое) направле­ние относительно квадрики f(K).

Теперь мы можем утверждать, что проведенное в § 2 разде­ление действительных прямых пространства Aⁿ(i) на шесть типов относительно данной квадрики имеет аффинный характер, а именно: справедлива

Теорема 4.3. Пусть в пространстве Aⁿ(i) заданы квадрика К, прямая П и аффинное преобразование f. Тогда прямая f(П) имеет относительно квадрики f(K) тот же тип (см. § 27.3), что и прямая П относительно квадрики К.

►Доказательство вытекает из теоремы 27.4 и того факта, что при аффинном преобразовании пространства A"(i) действительные точки переходят в действительные, а мнимые — в мнимые.◄

Докажем еще одну теорему, которая понадобится нам в даль­нейшем.

Теорема 4.4. Существует п линейно независимых векторов, имеющих неасимптотические относительно заданной квадрики (2) направления.

Как следует из § 22.4, существует преобразование координат x_i=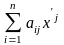 , i = 1, 2, … , n, (10) приводящее квадратичную форму , к нормальному виду

, , 0 < r ≤ n.

Запишем уравнение квадрики (2) в новом репере:

+2 = 0. (11)

На основании теоремы 2.3 мы можем искать векторы неасимпто­тических направлений исходя из уравнения (11), т. е. как векторы с′ (с′₁ ,с′₂, ..., с′_n), удовлетворяющие неравенству ≠ 0.

Очевидно, что векторы: с (1, 0, ..., 0, 0, ..., 0),

с₂ (0, 1, ..., 0, 0, ..., 0),

……………………..

c_r (0, 0, ..., 1, 0, ..., 0),

c_{r + 1} (1, 0, ..., 0, 1, ..., 0),

………………………

c_n (1, 0, ..., 0, 0, ..., 1)

удовлетворяют условию теоремы. ◄

Центр квадрики

Пусть в пространстве Aⁿ(i) выбран некоторый репер и задана квадрика уравнением +2 =0 (1)

Предположим, что точка B(b₁, b₂, ..., b_n)—центр квадрики (1) (см. § 25.8). Рассмотрим прямую x =b + c t, i=1, 2, ..., п, b , c R (2)

имеющую неасимптотическое направление. Как известно из § 27.3, прямая (2) имеет с квадрикой (1) две общие точки, различные или совпадающие. Для отыскания этих точек подставим значения х, из формул (2) в уравнение (1) и приведем подобные члены. Получим

t² +2t + q = 0, (3) где q = + 2 + a.

Если t и t — корни уравнения (3), то точками пересечения прямой (2) с квадрикой (1) будут: M (b + c t₁ , b₂ + c₂t₂ ..., b_п + с_п t₁)

M₂(b + c t₂, b₂ + c₂t₂, ..., b_n + c_nt₂).

Так как точка В является серединой отрезка М М₂, то (см. § 25.8)

b = = b + (t +t ), i=1, 2, … , n. (4)

Поскольку среди чисел c , c₂, ... , c (5)

есть отличные от нуля, то из равенств (4) следует, что t₁ +t₂ = 0. Но тогда в квадратном уравнении (3) коэффициент при первой степени t должен быть равен нулю, т. е. =0. (6)

Рассмотрим (6) как систему линейных однородных уравнений относительно неизвестных (5) (система состоит из одного уравне­ния). Она должна удовлетворяться для любого неасимптотического направления. Как известно из § 4, существует п линейно незави­симых решений этой системы, и, следовательно, ее ранг равен нулю, т. е. 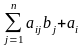= 0, i = 1, 2, … , n. (7)

Системе (7) должны удовлетворять координаты 6, любого цент­ра квадрики (1). Верно и обратное: любая точка В(b₁ ,b₂, ..., b_n), удовлетворяющая системе (7), является центром квадрики (1), так как из равенств (7) следуют равенства (4).

Перепишем систему (7) в виде = 0, i= 1, 2, ..., п. (8)

Итак, решения системы (8), и только они, являются координатами центров квадрики (1). Так как система (8) —линейная, то множест­во центров квадрики (1), если оно непустое, является плоскостью пространства A (i).

Определение 6.1. Квадрика, имеющая единственный центр, называется центральной.

Рассмотрим теперь плоскость A²(i). Пусть в некоторой аффинной системе координат задано уравнение линии второго порядка а₁₁x +2 а₁₂x₁x₂ + а₂₂x +2 а₁х₁ +2а₂х₂ + а = 0 (9)

Система уравнений для определения координат центра имеет вид

а₁₁ x₁ + a₁₂x₂ + a = 0, (10)

a _l2x₁ + a₂₂x₂ + a₂ = 0.

Так как для линий эллиптического и гиперболического типов определитель системы (10) ≠ 0,

то каждая из этих линий имеет единственный центр, т. е. является центральной линией. Таким образом, линии эллиптического и гипер­болического типов — центральные.

У параболы х — 2px = 0 нет центра, так как второе уравнение системы (10) дает p = 0, что противоречит определению параболы.

Для пары параллельных прямых х - а² = 0 (11)

система (10) сводится к одному уравнению х = 0. Отсюда следует, что каждая точка прямой, задаваемой этим уравнением, является центром линии (11), т. е. линия (11) имеет прямую центров. Это же справедливо для линии х = 0.