
- •Аффинное пространство и его простейшие свойства. Примеры.
- •Координаты в аффинном пространстве.
- •Плоскости в аффинном пространстве.
- •Аффинно-независимые точки аффинного пространства.
- •Векторное параметрическое уравнение плоскости. Плоскости и системы линейных уравнений.
- •Пересечение и сумма плоскостей аффинного пространства.
- •Аффинное отображение.
- •Изоморфизм аффинных пространств
- •Аффинные преобразования. Выражение аффинного преобразования в координатах.
- •Параллельный сдвиг аффинного пространства. Формулы параллельного сдвига. Центроаффинное отображение. Формулы центроаффинного отображения.
- •Фигуры в аффинном пространстве. Простое отношение трех точек. Отрезок. Середина отрезка. Центр фигуры.
- •Евклидово точечное пространство. Прямоугольная система координат.
- •Плоскости евклидова точечного пространства.
- •Гиперплоскость евклидова точечного пространства. Расстояние от точки до гиперплоскости. Объем параллелепипеда.
- •Движения евклидова точечного пространства. Группа движений евклидова точечного пространства. Метрически эквивалентные фигуры евклидова точечного пространства.
- •Собственные движения евклидовой точечной плоскости.
- •Движения трехмерного евклидова точечного пространства.
- •Несобственные движения евклидовой точечной плоскости. Аффинные преобразования евклидова точечного пространства.
- •Пространство An (I). Определение квадрики. Преобразование уравнения квадрики.
- •Пересечение квадрики с прямой.
- •Асимптотические направления. Центр квадрики.
- •Линии эллиптического, гиперболического и параболического типов. Центры линий второго порядка.
- •Диаметральные плоскости. Диаметры линий второго порядка.
Евклидово точечное пространство. Прямоугольная система координат.
Евклидово
пространство
 получается из n-мерного
действительного линейного пространства
путем введения в него скалярного
произведения. Пусть задано n-мерное
действительное аффинное пространство
, связанное с действительным линейным
пространством
.
Задавая на
скалярное произведение, т.е.превращая
его в пространство
, мы преобразуем аффинное пространство
в евклидово точечное пространство
. Итак, имеет место следующее
получается из n-мерного
действительного линейного пространства
путем введения в него скалярного
произведения. Пусть задано n-мерное
действительное аффинное пространство
, связанное с действительным линейным
пространством
.
Задавая на
скалярное произведение, т.е.превращая
его в пространство
, мы преобразуем аффинное пространство
в евклидово точечное пространство
. Итак, имеет место следующее
Определение 26.1. Аффинное пространство, связанное с евклидовым пространством , называется n-мерным евклидовым точечным пространством и обозначается .
В
n-мерном
пространстве
можно ввести ряд понятий, обобщающих
известные понятия в трехмерном
пространстве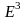 .
.
Определение
26.2. Репер
 (1) пространства
в случае ортонормированного базиса
(1) пространства
в случае ортонормированного базиса
 (2) будем называть прямоугольной
системой координат, а координаты точек
и векторов относительно такого репера
– прямоугольными.
(2) будем называть прямоугольной
системой координат, а координаты точек
и векторов относительно такого репера
– прямоугольными.
Так
как в любом ненулевом n-мерном
евклидовом пространстве
существуют ортонормированные базисы
(см. § 23.6), то в любом евклидовом точечном
пространстве
,n , существуют прямоугольные системы
координат.
, существуют прямоугольные системы
координат.
Пусть
в пространстве
заданы две прямоугольные системы
координат: (1) и
 (3)
(3)
Если
 -координаты
точки М
в репере (1),
-координаты
точки М
в репере (1),
 - координаты этой же точки в репере (3),
- координаты этой же точки в репере (3), ,- координаты точки О` в репере (1) и А=
-
матрица перехода от базиса (2) к базису
,- координаты точки О` в репере (1) и А=
-
матрица перехода от базиса (2) к базису
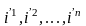 (4)
(4)
то,
как показано в § 25.2, старые координаты
точки М связаны с новыми координатами
этой точки формулами:


………………………………….. (5)
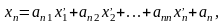
Использовав
обозначения (8) из § 25.2, можно записать
эти формулы в матричном виде: X=A (6)
(6)
Так как базисы (2) и (4) – ортонормированные, то матрица А в формуле (6) – ортогональная.
Определение 26.3. Расстоянием между точками М и N пространства называется длина вектора .
Итак,
обозначая указанное расстояние через
 ,
имеем
=
,
имеем
=
Если
заданы прямоугольные координаты точек
М и N:
М (
),
N( ),
то
=
),
то
=
Плоскости евклидова точечного пространства.
Так
как пространство
удовлетворяет аксиомам аффинного
пространства (см. определение 25.1), то в
существуют плоскости любой размерности
k,
где
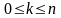 ,
причем нуль-мерные плоскости – это
точки, а единственная n-мерная
плоскость совпадает с пространством
. Очевидно, что всякая плоскость
,
причем нуль-мерные плоскости – это
точки, а единственная n-мерная
плоскость совпадает с пространством
. Очевидно, что всякая плоскость пространства
является k-мерным
евклидовым точечным пространством.
пространства
является k-мерным
евклидовым точечным пространством.
Возьмем
в пространстве
две одномерные плоскости, т.е. прямые
∆, ,.
Пусть а-
какой-либо направляющий вектор прямой
,.
Пусть а-
какой-либо направляющий вектор прямой
 и
-направляющий вектор прямой
.
и
-направляющий вектор прямой
.
Определение
26.4. Углом
между прямыми ∆ и
называется угол между их направляющими
векторами а,
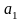 ,
т.е. число
,
определяемое формулой cos
,
т.е. число
,
определяемое формулой cos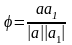 ,
,
Заметим,
что угол между прямыми
 и
не
зависит от выбора направляющих векторов
этих прямых.
и
не
зависит от выбора направляющих векторов
этих прямых.
Пусть
в пространстве
заданы две плоскости – плоскость
с начальной точкой М и направляющим
пространством
 и плоскость
и плоскость
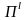 с начальной точкой N
и направляющим пространством
с начальной точкой N
и направляющим пространством
 .
.
Определение 26.5. Плоскости и называются ортогональными, если они имеют общую точку и каждый вектор из пространства ортогонален каждому вектору из пространства .
Лемма
10.
Если
плоскости
и
ортогональные, то они имеют только одну
общую точку. Док-во:
Пусть М`, N`-две
различные точки, принадлежащие и
плоскости
,
и плоскости
.
Тогда вектор
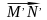 принадлежит
и пространству
,
и прострнству
,
поэтому
·
=0.
Но это невозможно, так как
принадлежит
и пространству
,
и прострнству
,
поэтому
·
=0.
Но это невозможно, так как
 .
.
Определение 26.6. Ортогональным дополнением плоскости пространства называется (n-k)-мерная плоскость, ортогональная плоскости .
Теорема 26.1. Если в пространстве задана плоскость , то через каждую точку N пространства проходит единственное ортогональное дополнение этой плоскости.
Док-во:
Пусть плоскость
задана начальной точкой М и направляющим
пространством
.
Рассмотрим ортогональное дополнение
(
)
подпространства
в пространстве
.
Пусть
 - плоскость в пространстве
с начальной точкой N
и направляющим пространством (
).
Так как
- плоскость в пространстве
с начальной точкой N
и направляющим пространством (
).
Так как
 , то согласно теореме 25.7, плоскости
и
имеют общую точку. Итак,
- искомое ортогональное дополнение
плоскости
.
, то согласно теореме 25.7, плоскости
и
имеют общую точку. Итак,
- искомое ортогональное дополнение
плоскости
.
Единственность ортогонального дополнения плоскости следует из того, что каждая плоскость однозначно определяется заданием какой-либо ее точки и направляющего пространства.
Рассмотрим
(n-1)-мерную
плоскость, т.е. гиперплоскость
 и прямоугольную систему координат
и прямоугольную систему координат
(O, ). (1)
Пусть
 (
( )
- некоторая точка гиперплоскости
и
)
- некоторая точка гиперплоскости
и
 - направляющее пространство для
. Согласно теореме 26.1, через точку
проходит одномерное ортогональное
дополнение плоскости
,
т.е. прямая ∆ . Пусть n(
- направляющее пространство для
. Согласно теореме 26.1, через точку
проходит одномерное ортогональное
дополнение плоскости
,
т.е. прямая ∆ . Пусть n( )-
какой-либо направляющий вектор прямой
∆ и М (
)-
какой-либо направляющий вектор прямой
∆ и М ( )-
произвольная точка пространства
. Точка М принадлежит плоскости
тогда и только тогда, когда векторы n
и
ортогональны, т.е.
=0.
Записывая это равенство в координатах,
получаем
)-
произвольная точка пространства
. Точка М принадлежит плоскости
тогда и только тогда, когда векторы n
и
ортогональны, т.е.
=0.
Записывая это равенство в координатах,
получаем
 (2)
(2)
Этому
уравнению относительно
удовлетворяют координаты любой точки
плоскости
,
и только такой точки. Другими словами,
уравнение (2) является уравнением
плоскости
.
Отметим, что эта плоскость проходит
через точку
(
)
и ортогональна вектору n(
),
т.е. прямой с направляющим вектором n.
Запишем уравнение (2) гиперплоскости
в виде
 (3)
(3)
Пусть N( ) - произвольная точка пространства .Рассмотрим прямую , проходящую через точку N и являющуюся ортогональным дополнением гиперплоскости . Эта прямая пересекает гиперплоскость в некоторой точке Р( ).
