6. Пересечение и сумма плоскостей аффинного пространства.

Определение 7. Пусть - n-мерное аффинное пространство, связанное с векторным пространством , – плоскость с направляющим пространством , проходящая через точку , – плоскость с направляющим пространством , проходящая через точку . Плоскости и называются пересекающимися, если они имеют по крайней мере одну общую точку.

Теорема 7. Пусть – n-мерное аффинное пространство, связанное с векторным пространством , – плоскость с направляющим пространством , проходящая через точку , – плоскость с направляющим пространством , проходящая через точку . Тогда

1) плоскости и пересекаются тогда и только тогда, когда , где – сумма подпространств и линейного пространства ;

2) если плоскости и пересекаются, то их пересечением является плоскость с направляющим пространством .

Определение 8. Суммой плоскостей и аффинного пространства называется их аффинная оболочка, т.е. плоскость наименьшей размерности, содержащая плоскости и . Обозначается .

Теорема 8. Пусть – аффинное пространство, связанное с векторным пространством над полем ; и – плоскости размерности k и l соответственно из с направляющими пространствами и ; Пусть т – размерность пересечения . Тогда размерность суммы плоскостей и равна , если эти плоскости пересекаются,

и , если они не пересекаются.

Док-во: 1) Пусть плоскости П^k и П^l пересекаются и О – их общая точка. Если принять эту точку за начало отсчета радиусов-векторов, то множествами радиус-векторов точек плоскостей П^k , П^l и П^k П^l являются соответственно V^k , V^l и V^k V^l. Но тогда формула (8) следует из теоремы 17.8.

2)Пусть теперь плоскости П^k и П^l не пересекаются. Рассмотрим одномерное подпространство пространства V ⁿ и подпространство S = V^k + V^l +T. Согласно теореме 25.7, V^k + V^l, поэтому dim S = k + l – m + 1. Очевидно, что плоскость П с начальной точкой М₀ и направляющим пространством S содержит каждую из плоскостей П^k и П^l. С другой стороны, любая плоскость, которой принадлежит плоскости П^k и П^l, содержит плоскость П. Итак, П – аффинная оболочка плоскостей П^k и П^l, и , следовательно , формула (9) доказана.

Определение 9. Характеристикой пары плоскостей и аффинного пространства называется упорядоченный набор чисел , где s – размерность суммы плоскостей и , а – размерность пересечения их направляющих пространств.

Замечание. Без ограничения общности можно считать, что . Тогда .

Определение 10. Непересекающиеся плоскости и с характеристикой называются:

1) параллельными, если ;

2) частично параллельными, если ;

3) скрещивающимися, если .

7. Аффинное отображение.

Пусть и - аффинные пространства, связанные соответственно с линейными пространствами и над полем P.

Определение 11. Отображ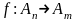ение называется аффинным, если существует линейное отображение 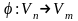такой, что для любых точек . Отображение называется однородной частью отображения f.

Теорема 25.9. Для любого линейного оператора (2) и любых точек M , существует единственное аффинное отображение (1), такое, что - его однородная часть и M₁ = f (M).

Док-во: Предположим, что искомое отображение (1) существует. Возьмём произольную точку .Тогда в силу равенства (3) имеем f = .

В силу аксиомы из определения 25.1 существует единственная точка , такая, что f(N)=N₁ .

Итак, если искомое отображение (1) существует, то оно единственно. Теперь докажем существование отображения, построив его следующим образом. Для произвольной точки определим ее образ N₁ при искомом отображении f с помощью равенства =

Это возможно в силу аксиомы 1⁰ из определения 25.1. Покажем теперь, что построенное отображение f удовлетворяет условию ( ) =f для любых точек K,L . Имеем = = =- =- = .

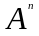Теорема 25.10.Пусть -система аффинное независимость точек пространства , а - произвольная система точек пространства . Тогда существует единственное аффинное отображение (1), удовлетворяющее условиям f ).