1. Источники ЭДС и источники тока.

Источник электрической энергии характеризуется ЭДС Е и внутренним сопротивлением R_n . Если через него под действием ЭДС Е протекает ток I, то напряже­ние на его зажимах

U = Е - IR_n при увеличении I уменьшается.

1. Если у некоторого источника внутреннее сопротивление R_n = 0, то ВАХ ( вольтамперная характеристика ) его будет прямой линией. Такой харак­теристикой обладает идеализированный источник питания, называемый источником ЭДС. Следовательно, источник ЭДС представ­ляет собой такой идеализированный источник питания, напряже­ние на зажимах которого постоянно (ие зависит от тока I ) и равно ЭДС Е, а внутреннее сопротивление равно нулю.

2. Если у некоторого источника беспредельно увеличивать ЭДС Е

и внутреннее сопротивление R_n то точка с (рис.) отодвигает­ся по оси

абсцисс в бесконечность, а угол α стремится к 90⁰. Такой источник

питания называют источником тока. Следовательно, источник тока

представляет собой идеализиро­ванный источник питания, который

создает ток J = I, независящий от сопротивления нагрузки, к которой

он присоединен, а его ЭДС Е_ит и внутреннее сопротивление R_n равны

бесконечности. Отноше­ние двух бесконечно больших величин Е_ит /R_ит равно конечной величине — току J источника тока.

При расчете и анализе электрических целей реальный источник электрической энергии с конечным значением R_В, заменяют расчет­ным эквивалентом. В качестве эквивалента может быть взят:

а)источник ЭДС Е с последовательно включенным сопротивле­нием R_n , равным внутреннему сопротивлению реального источника;

б) источник тока с током J = E / R_n , и параллельно с ним включен­ным сопротивлением R_В. I = E / ( R + R_в ).

Каким из двух расчетных эквивалентов пользоваться, совер­шенно безразлично. В дальнейшем используется в основном пер­вый эквивалент. Обратим внимание на следующее:

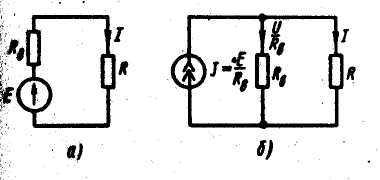1) источник ЭДС и источник тока — идеализированные источни­ки, физически осуществить которые, строго говоря, невозможно;

2) схема рис. б эквивалента схеме рис. а в отношении

энергии, выделяющейся в сопротивлении нагрузки R,

и не эквива­лентна ей в отношении энергии,

выделяющейся во внутреннем .со­противлении источника

питания R_В;

3) идеальный источник ЭДС без последовательно соединенного с ним R_В, нельзя заменить идеальным источником тока.

2. Замена реального источника тока эквивалентным.

На примере схемы (а) на рисунке осуществим эквивалентный пере­ход от схемы с источником тока к схеме с источником ЭДС. В схеме рисунка (б) источник тока дает ток J = 50 А. Шунтирующее его сопротивление R_В = 2 Ом. Найти ЭДС эквивалентного источника ЭДС в другой схеме. Решение: ЭДС Е = JR_В =100 В. Следовательно, параметры эквивалентной схемы таковы: Е = 100 В, R, = 2 Ом.

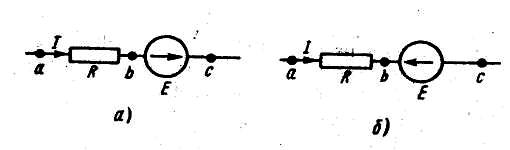3. Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома. Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φ_а — φ_с ) на концах участка цепи и имеющейся на этом участке ЭДС Е. Так, по

уравнению для схемы (а) I = ( φ_a – φ_c + E) / R =

( U_ac +E ) / R. Для схемы (б) I = ( φ_a – φ_c - E) / R =

( U_ac +E ) / R. В общем случае:

I = ( φ_a – φ_c ± E) / R = ( U_ac ± E ) / R. Это

уравнение математически выражает закон Ома для участка цепи, содержащего ЭДС.

4. Законы Крирхгофа.

Первый закон Кирхгофа можно сформулировать двояко: 1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю; 2) сумма подтекающих к любому узлу токов равна сумме утека­ющих от узла токов. Физически мерный закон Кирхгофа означает, что движение за­рядов в цепи происходит так, что ни и одном из узлов они не скапливаются. Второй закон Кирхгофа также можно сформулиро­вать двояко:

1) алгебраическая сумма падений напряжения в любом замкну­том контуре равна алгебраической сумме ЭДС вдоль того же кон­тура: ∑ IR = ∑Е. 2) алгебраическая сумма напряжений (не падений напряже­ния!) вдоль любого замкнутого контура равна нулю:

∑ U = 0. Законы Кирхгофа справедливы для линейных и нелинейных це­пей при любом характере изменения во времени токов и напряже­ний.

5. Потенциальная диаграмма.

Под потенциальной диаграм­мой понимают график распределения потенциала вдоль какого-ли­бо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.

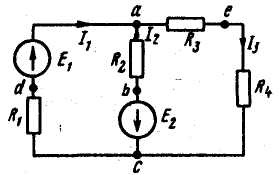
Пример. Построить потенциальную диаграмму для контура

аЬсеа на рисунке: ( E₁ = 80V, E₂ = 64 V, R₁ = 6 Om, R₂ = 4Om,

R₃ = 3 Om, R₄ = 1 Om.) Решение. Подсчитаем суммарное

сопротивление контура: 4 + 3 + I — 8 Ом. Выберем масштабы

по оси абсцисс (ось х) и по оси ординат (ось у). Произвольно

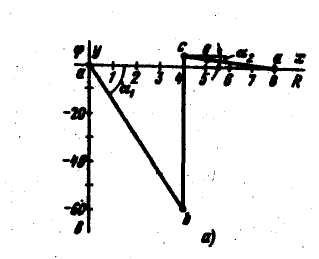примем потенциал одной из точек, например точки а,

φ_а = 0. Эту точку на диаграмме поместим в начало координат.

Потенциал точки b: φ_b = φ_a + I₂4 = φ_a – 60 = -60 В; ее координаты:

Х = -4. Y = -60. Потенциал точки с: φ_c = φ_b + E₂ ; ее координаты:

X = 4, Y = 4. Потенциал точки е: φ_e = φ_c + I₃R₄ = 4 -1=3;

ее координаты: X = 5; Y = 3. Тангенс угла а₁ наклона прямой

a_ab к оси абсцисс пропорционален току I₂, а тангенс угла а₂ наклона

прямой cе — току I₃, tg α = I*m_r / m_φ, где m_r и m_φ –масштабы по осям Х и У.

Обратим внимание на различие в знаках, с которыми входит падение напряже­ния IR при определении потенциала какой-либо точки схемы через потенциал исход­ной точки и при составлении уравнений но второму закону Кирхгофа. При вычисле­нии потенциала последующей точки через потенциал предыдущей IR берут со знаком минус, если перемещение по сопротивлению R совпадает по направлению с током, тогда как при составлении уравнений по второму закону Кирхгофа IR неко­торого участка цепи берут в сумме ∑1R со знаком плюс, если обход этого участка совпадает с направлением тока I на нем.

6. Энергетический баланс в цепях.

При про­текании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, вы­деляющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником пита­ния. Если направление тока I, протекающего через источник ЭДС Е, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени (мощность), равную EI, и произве­дение EI входит в уравнение энергетического баланса с положи­тельным знаком. Если же направление тока I встречно направлению ЭДС E, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение EI войдет в уравнение энергетического баланса с отрицательным знаком.

Уравнение энергетического баланса при питании только от ис­точников ЭДС имеет вид

∑I²R = ∑EI. Когда схема питается не только от источников ЭДС, но и от источников тока, т. е. к отдельным узлам схемы подтекают и от них утекают токи источников тока, при составлении уравнения энерге­тического баланса необходимо учесть и энергию, доставляемую источниками тока. Допустим, что к узлу а схемы подтекает ток I от источника тока, а от узла b этот ток утекает. Доставляемая источ­ником тока мощность равна U_abJ. Напряжение U_ab и токи в ветвях схемы должны быть подсчитаны с учетом тока, подтекающего от источника тока. Последнее проще всего сделать по методу узловых потенциалов. Общий вид уравнения энергетического баланса: ∑I²R = ∑EI + ∑ U_abJ.

7. Метод пропорциональных величин.

Согласно методу про­порциональных величин, в самой удаленной от источника ЭДС вет­ви схемы (исходной ветви) произвольно задаемся некоторым током, например током в 1 А. Далее, продвигаясь к входным зажимам, находим токи в ветвях и напряжения на различных участках схемы. В результате расчета получим значение напряжения U_mn схемы и токов в ветвях, если бы в исходной ветви протекал ток в 1 А.

Так как найденное значение напряжения U_mn в общем случае не равно ЭДС источника, то следует во всех ветвях изменить токи, умножив их на коэффициент, равный отношению ЭДС источника к найденному значению напряжения в начале схемы. Метод пропорциональных величин, если рассматривать его обо­собленно от других методов, применим для расчета цепей, состоя­щих только из последовательно и параллельно соединенных сопро­тивлений и при наличии в схеме одного источника. Однако этот метод можно использовать и совместно с другими методами.

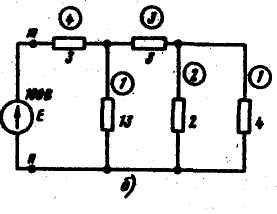
Пример. Найти токи и ветвях схемы рисунке методом

пропорциональных величин. Сопротивления схемы даны

в омах. Решение. Задаемся током в ветви с сопротивлением

4 Ом, равным 1 А, и подсчитываем токи в остальных ветвях

(числовые значения токов обведены на ри­сунке кружками).

Напряжение между точками мил равно I*4 + 3*3 + 4*3 = 25 В.

Так как ЭДС Е = 100 В, все токи следует умножить на коэффициент К = 100/25 = 4.

8. Метод контурных токов.

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контур­ных токов, после чего через них определяют токи ветвей. Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирх­гофа.

Общий вид уравнения метода контурных токов:

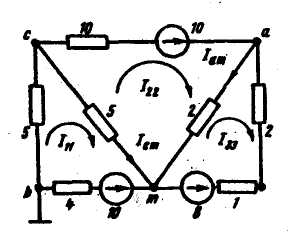
Пример. Найти токи в схеме методом контурных токов.

Числовые значения сопротивлений номах и ЭДС в вольтах

указаны на рисунке. Решение. Выберем направления всех

контурных токов I₁₁, I₂₂, I₃₃, по часовой стрелке. Определяем: R₁₁ = 5+5+4=14 Om, R₂₂ = 5+10+2=17 Om, R₃₃ = 2+2+1=5 Om, R₁₂ = R₂₁ = -5 Om, R₁₃ = R₃₁ = 0, R₂₃ = R₃₂ = -2 Om, E₁₁ = -10 V, E₃₃ = -8 V. Запишем систему уравнений: 14I₁₁ – 5I₂₂ = -10,

-5I₁₁ +17I₂₂ – 2I₃₃ = 10, -2I₂₂ +5I₃₃ = -8. Определитель системы: 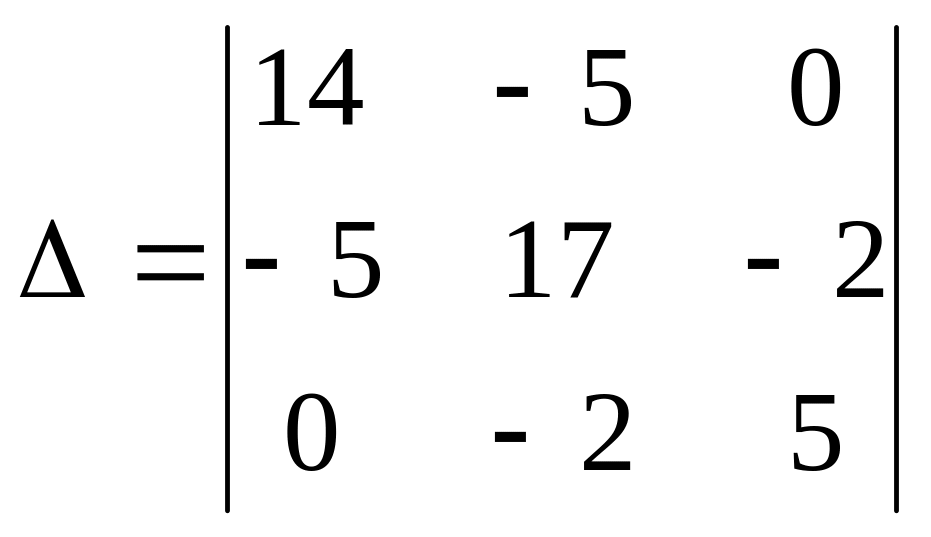=1009, подсчитаем токи: I₁₁ = 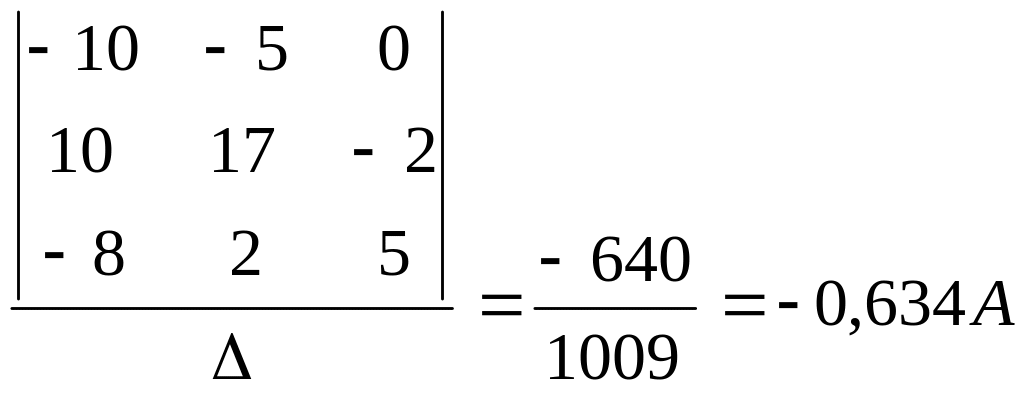. I₂₂ = 0,224A, I₃₃ = -1,51A. Ток в ветви

cm I_cm = I₁₁ – I₂₂ = - 0,634 – 0,224 = - 0,86A. Ток в ветви am I_am = I₂₂ – I₃₃ = 0,224 + 1,51 = 1,734A.

9. Принцип и метод наложения.

Исходная формула: . Чтобы составить, общее выражение для тока в к-ветви сложной схемы, составим уравнения по методу контурных токов, выбрав контуры так, чтобы к-ветвь входила только в один к-контур (это всегда возможно). Тог­да ток в л-ветви будет равен контурному току I_кк. Каждое слагаемое представляет собой ток, вы­званный в к-ветви соответствующей контурной ЭДС. Например, Е₁₁∆_к1 / ∆ есть составляющая тока к-ветви, вызванная контурной ЭДС Е₁₁. Каждую из контурных ЭДС можно выразить через ЭДС ветвей Е₁, Е₂.., сгруппировать коэффициенты при этих ЭДС и получить выражение следующего вида:

. Это уравнение выражает собой принцип наложения.

Принцип наложения формулируется следующим образом: ток в k-ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных электрических цепей. Принцип наложения положен в основу метода расчета, получив­шего название метода наложения.

При расчете цепей данным методом поступают следующим об­разом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов.

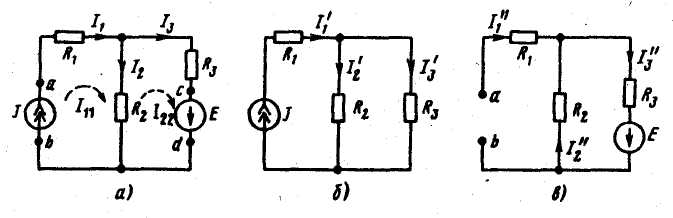Пример. Для схемы на рисунке,

а методом наложения найти токи в

ветвях, определить мощности,

отдаваемые в схему источникам

тока и источником ЭДС, полагая

R₁ = 2 Ом; R₂ = 4 Ом; R₃ = 6 Ом;

J = 5 А; E = 20 В.

Решение. Положительные направления токов в ветвях принимаем в соответ­ствии с рис. а. С помощью схемы рис.б (источник ЭДС удален, и зажимы cd закорочены) найдем токи в ветвях от действия источника тока: I^/₁ = J =5A, I^/₂ = I^/₁R₃ / R₂ +R₅ = 5*6 / (4+6) = 3A,

I^/₃ = 2A. Используя схему рис. в, подсчитываем токи в ветвях от действия источника ЭДС (зажимы ab разомкнуты, так как внутреннее сопротивление источника тока равно бесконечности): I"₁ = 0; I"₂ = I"₃ = E / ( R₂ + R₃ ) = 2А. Результирующие токи в ветвях вычислим, алгебраически суммируя соответствующие частичные токи этих двух режимов: I₁ = I^/₁ + I^/₂ = 5 + 0 = 5А; I₂ = I'₂ - I"₂ = 3 - 2 = 1 А; Iз = I'₃ + I"₃ = 2 + 2 = 4А;

φ_a = φ_b + I₂R₂ + I₁R₁; U_ab = 1*4 + 5*2= 14 В. Мощность, отдаваемая в схему источником тока, U_abJ = 14*5 = 70 Вт. Мощ­ность, отдаваемая в схему источником ЭДС, EI₃ = 20*4 = 80 Вт. Уравнение баланса мощности: .

10. Входные и взаимные проводимости ветвей. Входное сопротивление.

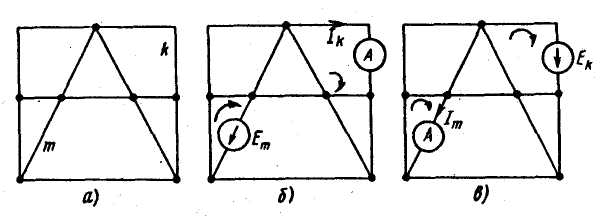На рис.а изображена так называемая

скелетная схема пассивной цепи. На ней

показаны ветви и узлы. В каждой ветви

имеется сопротивление. Выделим в

схеме две ветви: m и k. Поместим в

ветвь m ЭДС Е_m (других ЭДС в схеме

нет). Выберем контуры в схеме так,

чтобы k-ветвь входила только в k-контур, а m-ветвь — только в m-контур. ЭДС Е_m вызовет токи в ветвях k и m: I_k = E_mg_km, I_m = g_mm. Коэффициенты g имеют размерность проводимости. Коэффициенту с одинаковыми индексами (g_mm) называют входной проводимостью ветви (ветви m). Он численно равен току в ветви m, возникшему от действия ЭДС E_m = 1В (единичной ЭДС): I_m = 1*g_mm. Коэффициенты g с разными индексами называют взаимными проводимостями. Так, g_km есть взаимная проводимость к- и m -ветвей. Взаимная проводимость g_km численно равна току в k -ветви, возникающему от действия единичной ЭДС в m -ветви. Входные и взаимные проводимости ветвей используют при вы­воде общих свойств линейных электрических цепей и при расчете цепей по методу наложения. Входные и взаимные проводимости могут быть определены рас­четным и опытным путями. При их расчетном определении составляют уравнения по мето­ду контурных токов, следя за тем, чтобы ветви, взаимные и входные проводимости которых представляют интерес, входили каждая только в свой контур. Далее находят определитель системы А и по нему необходимые алгебраические дополнения:

g_mm = ∆_mm / ∆, g_km = ∆_km / ∆. По формуле g_km может получиться либо положительной, либо отрицательной величиной. Отрицательный знак означает, что ЭДС Е_m направленная согласно с контурным током в m-ветви, вызывает ток в k-ветви, не совпадающей по направлению с произвольно выбранным направлением контурного тока I_к по k-ветви.

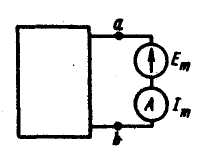При опытном определении g_mm и g_km в m-ветвь схемы включают источник ЭДС Е_m, а в k-ветвь — амперметр. Поделим ток I_k на ЭДС Е_m и найдем значение g_km. Для определения входной проводимости ветви m(g_mm) необходимо измерить ток в m-ветви, вызванной ЭДС Е_m. Частное от деления тока m-ветви на ЭДС m-ветви и дает g_nm.

Выделим m-ветвь, обозначив всю остальную часть схемы

(не содержащую ЭДС) некоторым прямоугольником (рис.). Вся cхема,

обозначенная прямоугольником, по отношению к зажимам ab обладает

некоторым сопротивлением. Его называют входным сопротивлением.

Входное сопротивление m-ветви обозначим R_BXm. Тогда R_BXm = E_m / I_m = 1 / g_mm = ∆ / ∆_mm.

Таким образом, входное сопротивление m-ветви есть величина, обратная входной проводимости этой ветви.

Пример. Определить входную g₁₁ и взаимную g₁₂

проводимости в схеме на рисунке. Решение. Контуры в схеме

выбраны так, что ветвь 1 (ветвь cbm) с источником ЭДС

Е₁ входит только в первый контур, а ветвь 2 (ветвь са) с

источником ЭДС Е₂ — во второй. Поэтому можно

воспользоваться определителем системы ∆ и алгебраическими

дополнениями ∆₁₁ и ∆₁₂, составленными по данным: R₁₁ = 5+5+4=14 Om, R₂₂ = 5+10+2=17 Om, R₃₃ = 2+2+1=5 Om, R₁₂ = R₂₁ = -5 Om, R₁₃ = R₃₁ = 0, R₂₃ = R₃₂ = -2 Om, E₁₁ = -10 V, E₃₃ = -8 V. g₁₂ = ∆₁₂ / ∆ = 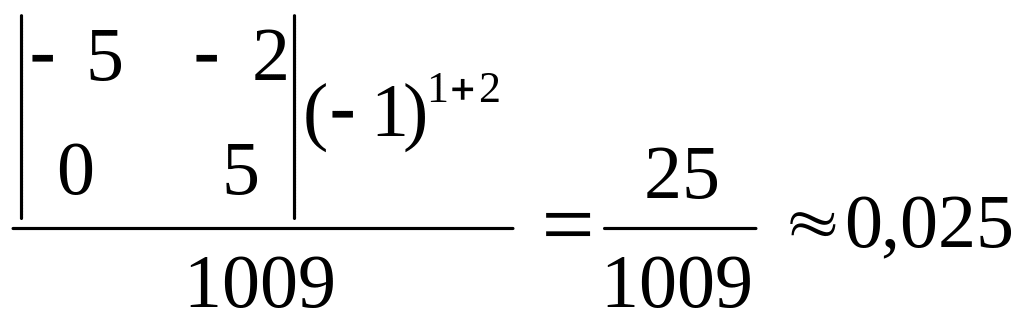Ом^-1 ≈ 0,025 См, g₁₁ = ∆₁₁ / ∆ = 0,081 Ом^-1 .

11. Теорема взаимности.

Теорема формулируется следующим образом: для любой линейной цепи ток в к –ветви, вызванный источником ЭДС Е_m, находящимся в m –ветви, I_k = E_mg_km равен току I_m в m –ветви, вызванному источником ЭДС E_k ( численно равный ЭДС E_m ), находящимся в k –ветви, I_m = E_kg_mk. Доказательство: Так как Е_m = E_k, а матрица симметрична, то I_k = I_m.

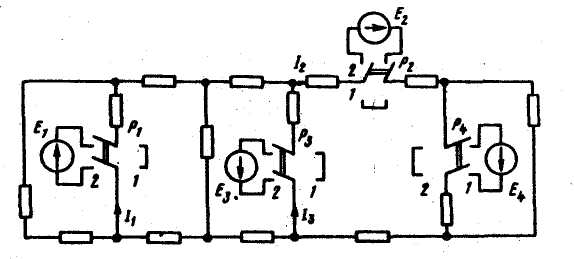Пример. В схеме на рисунке переключатели

Р₁ , Р₂ , Р₃ , Р₄ могут находиться в первом или

во втором положении. Если они находятся в

положении 1, то в схеме включен только один

источник ЭДС Е₄. Под действием ЭДС Е₄

протекают токи I₁ = 1,5А, I₂ = 3A, I₃ = 1А.

Найти ток U, если все переключатели находятся

в положении 2, полагая, что E₁ = 20 В, E₂ = 40 В, Е₃ = 50 В, E₄ =10 В.

Решение: Для определения тока I₄ воспользуемся принципом наложения и принципом взаимности. Если бы в схеме был включен один источник ЭДС Е₁ , = 10 В; а остальные (Е₂ и Е₃ ) отсутствовали, то в ветви 4 но принципу взаимности протекал бы сверху вниз ток в 1,5 А. Так как ЭДС Е₁ = 20 В, то в ветви 4 протекает ток, равный 1,5*20/10 = 3 А. Аналогичным образом найдем токи в ветви 4 при включении источников ЭДС Е₂ и Е₃ и произведем алгебраическое сложение частичных токов (с учетом их направлении):

I₄ = 1,5*20/10 + 3*40/10 – 1*50/10 = 10A.

12. Теорема компенсации.

Рассмотрим два варианта этой теоремы. В любой электрической цепи без изменения токораспределения сопротивление можно заменить: I) источником ЭДС, ЭДС которого численно равна падению напряжения на заменяемом со­противлении и направлена встречно току в этом сопротивлении; 2) источником тока J, ток которого численно равен току в этом сопро­тивлении и имеет то же направление, что и ток I. Для доказательства теоремы компенсации выделим из схемы одну ветвь с сопротивлением R, по которой течет ток I, а всю осталь­ную часть схемы условно обозначим прямоугольником ( рис. а ). Если в выделенную ветвь включить два одинаковых и противо­положно направленных источника ЭДС Е, ЭДС которых равна па­дению напряжения на сопротивлении Р под действием тока I (Е = IR, рис. б ), то ток I в цепи от этого не изменится. Если φ_c = φ_a то точки а и с можно объединить в одну, т. е. закоротить участок ас и получить схему, в которой вместо сопротивления R включен источник ЭДС Е.

Схема, соответствующая второму

варианту теоремы, изображе­на на рис. г.

Чтобы прийти к ней, заменим

последовательно соединенные R и Е, на

участке ас (рис. б ) параллельным

соеди­нением источника тока J = E / R = I и сопротивления R. Так как U_ac = О, то ток через R будет отсутствовать и потому R можно удалить из схемы. Если ЭДС Е участка bc включить в состав источника тока, тo получим схему рис. г, где напряжение U_ba = -IR.

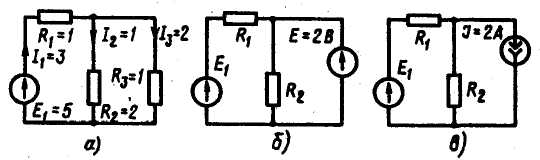Пример. На схеме рисунке а даны

значения R(Ом), ЭДС E (В) и токов

I(А). Заменить R₃ источником ЭДС

и источником тока. Решение. На

рис.б изображена схема с источником

ЭДС Е = 2В, а на рис. в — с источником тока J = 2А.

13. Линейные соотношения в электрических цепях.

Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной ветви, то две любые величины (токи и напряже­ния) двух любых ветвей связаны друг с другом линейными зависи­мостями вида y = а + bх. Функцию х выполняет ток или напряжение одной ветви, функ­цию у — ток или напряжение другой ветви. Согласно методу контурных токов, об­щее выражение для тока в k-ветви записывается в виде: . Если в схеме изменяется только одна ЭДС, например ЭДС Е_m, то все слагаемые в формуле, кроме слагаемого E_mg_km, постоянны и могут быть для сокращения записи заменены некоторым слагаемым А_к. Сле­довательно, I_k = A_k + E_mg_km . Аналогично, для p-ветви: I_p = A_p + E_ng _pm. Найдем E_m : Е_m = (I_Р — A_P) / g_pm и получим: I_k = a_k + b_kI_p, где а_к = А_k – А_pg_km = g_km/g_pm.

Это равенство свидетельствует о том, что при изменении ЭДС E_m токи I_к и I_p связаны линейной зависимостью. Из теоремы компен­сации известно, что любое сопротивление можно заменить источником ЭДС. Следовательно, изменение сопротивления в m-ветви эквивалентно изменению ЭДС Е_m. Таким образом, линейное соотношение между двумя любыми токами имеет место при изменении не только ЭДС Е_m, но и сопротивления какой-то m-ветви.

Коэффициенты а_к и b_к могут быть найдены расчетным или опытным путем. При опытном определении коэффициентов достаточно найти значения двух токов (соответственно напряжений) при двух различ­ных режимах работы схемы и затем решить систему из двух урав­нений с двумя неизвестными. Пусть, например, в первом опыте: I_k = I_k1, I_p = I_p1, а во втором: I_k = I_k2, I_p = I_p2. Тогда: I_k1 = a_k + b_kI_p1, I_k2 = a_k + b_kI_p2, отсюда: и .

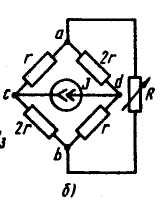
Пример. В схеме на рисунке сопротивление R изменяется от нуля до

беско­нечности. Вывести зависимость напряжения U_cd от напряжения U_ak.

Решение. При разомкнутой ветви ab U_cd = 1,5rJ и U_ab = 0,5rJ. При коротком

замыкании ветви ab U_cd = 3/4 rJ и U_ab = 0. Отсюда а = 4/3 rJ и b = 1/3. Тогда,

Ucd = 4/3 rJ + 1/3 Uab.

14. Замена нескольких параллельных ветвей, содержащих источники тока и ЭДС, одной эквивалентной.

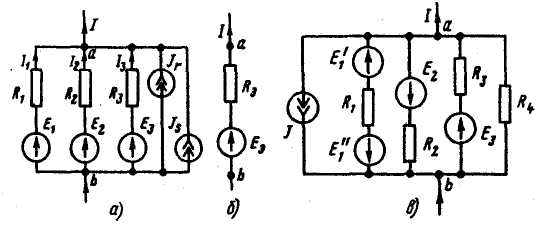
Участок цепи на рис. б эквивалентен участку цепи

на рис. а, если при любых значениях тока I,

подтекающего из всей остальной, не показанной на

рисунке части схемы, напряжение на зажимах а и b

(U_ab) в обеих схемах одинаково. Для того чтобы

выяснить, чему равняются R_э и Е_э, составим

уравнения для обеих схем. Для схемы рис. а:

I₁ + I₂ + I₃ + J_r + J_s = I, I₁ = ( E₁ – U_ab ) / R₁ = ( E₁ – U_ab)g₁ ; I₂ = ( E₂ – U_ab )g₂ , I_n = ( E₂ – U_ab )g_n

Следовательно: I = ∑I_k = ∑E_kg_k + ∑J_k - U_ab∑gk. Для схемы рис. б: I = E_эg_э – U_abg_э. Равенство токов I в схемах на рис. а, б должно иметь место при любых значениях U_ab, а это возможно только в том случае, если: g_э = ∑g_k , тогда: ∑E_kg_k + ∑J_k = E_эg_э, отсюда:

При подсчетах по этой формуле следует иметь в виду следую­щее: 1 )если в какой-либо ветви схемы ЭДС отсутствует, то соответ­ствующее слагаемое в числителе формулы выпадает, но проводимость этой ветви в знаменателе остается; 2) если какая-либо ЭДС в исходной схеме имеет направление, обратное изображенному на рис. а, то соответствующее слагаемое войдет в числитель фор­мулы со знаком минус.

Пример. Заменить параллельные ветви рис. в одной эквивалентной. Дано: E₁^/ =10В; E₁^// = 30В; E₂ = 40В; E₃ = 60В; R₁ =2Ом; R₂ = 4Ом; Rз= 1Ом; R₄ = 5Ом; J =6А.

Решение. Находим: g₁ = 0,5 См; g₂ = 0,25 См; g₃ = 1 См; g₄ = 0,2 См; R_э = 1 / ∑g_k = 1 / ( 0,5 + 0,25 + 1 + 0,2 ) = 0,513 См; Е_э = ( ∑E_kg_k – J ) / ∑g_k = (( 10 – 30 )*0,5 – 40*0,25 + 60 -6) / 1,95 = 18,4В

15. Метод узловых потенциалов.

Ток в любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических це­пей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов.

Допустим, что в схеме п узлов. Так как любая (одна) точка схемы может быть заземлена без изменения токораспределения в ней, один из узлов схемы можно мысленно заземлить, т. е. принять по­тенциал его равным нулю. При этом число неизвестных уменьшает­ся с п до п – 1. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Киргофа. В том случае, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод явля­ется более экономным, чем метод контурных токов.

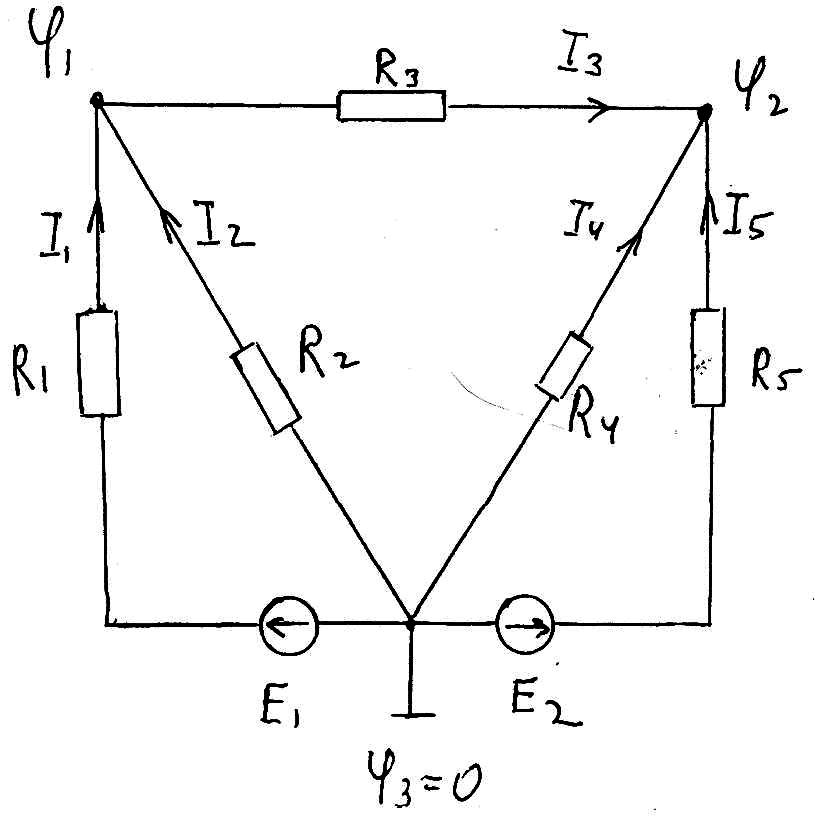
Пример. Запишем уравнения с помощью законов Кирхгофа.

I1 + I2 + I3 = 0	I11 = I1
I3 + I4 + I5 = 0	I22 = I3
R1I1 – R2I2 = E1	I33 = -I5
R2I2 + R3I3 – R4I4 = 0		I2 = I22 – I11
R4I4 – R5I5 = -E5		I4 = I33 – I22

R₁I₁₁ – R₂( I₂₂ – I₁₁ ) + 0 = E₁

R₂( I₂₂ – I₁₁ ) + R₃I₂₂ – R₄( I₃₃ – I₂₂ ) = 0

0 + R₄( I₃₃ – I₁₁ ) + R₅I₃₃ = -E₅

φ₁ = φ₃ + E₁ – R₁I₁, след: I₁ = ( E₁ + φ₃ – φ₁ )g₁. φ₁ = φ₃ – R₂I₂, след: I₂ = ( φ₃ – φ₁ )g₂. Подобно:

I₃ = ( φ₁ – φ₂ )g₃, I₄ = ( φ₃ – φ₂ )g₄, I₅ = ( E₅ + φ₃ – φ₂ )g₅

Получим систему уравнений: ( E₁ – φ₁ )g₁ + ( -φ₁ )g₂ – ( φ₁ – φ₂ )g₃ = 0

( φ₁ – φ₂ )g₃ + ( -φ₂ )g₄ + ( E₅ – φ₂ )g₅ = 0. Используем матрицы

, Gφ = I, тогда φ = G^-1I. Так можно найти потенциалы.

16. Метод двух узлов.

Часто встречаются схемы, содержащие всего два узла; на рис.

изображена одна из таких схем. Наибо­лее рациональным

методом расчета токов в них является метод двух узлов. Под

методом двух узлов понимают метод расчета электриче­ских цепей,

в котором за искомое (с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы. Расчетные формулы этого метода получают на основе формул I_n = ( E₂ – U_ab )g_n и I = ∑I_k = ∑E_kg_k + ∑J_k - U_ab∑gk; их также можно получить из метода узловых потенциалов.

В схеме ток I к узлам а и b схемы не подтекает. Поэтому если в предыдущей формуле принять I = 0, то из нее может быть найдено напряжение между двумя узлами:

U_ab = ( ∑E_kg_k + ∑I_k ) / ∑g_k. После определения напряжения U_ab находят ток в любой (n-й) ветви по формуле I_n = (E_n -U_ab )g_n.

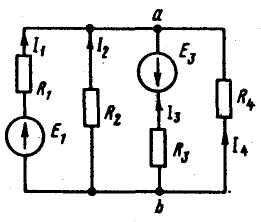
Пример. Найти токи в схеме на рисунке, и сделать проверку баланса мощности, если Е = 120 В, Е₃ = 50 В, R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 1 Ом, R₄ = 10 Ом. Решение. Определим токи в схеме на рисунке: U_ab = ( 120*0,5 – 50*1) / ( 0,5 + 0,25 + 1 + 0,1 ) = 10 / 1,85 = 5,4 В;

I₁ = ( E₁ - U_ab) / R₁ = (120 - 5,4) / 2 = 57,3 А; I₂ = (Е₂ - U_ab) / R₂ = (0 - 5,4) / 4 = -1,35 A;

I₃ = -55,4 А; I₄ = - 0,54 А. В схеме потребляется мощность I₁²R₁ + I₂²R₂ + I₃²R₃ + I₄²R₄ = 57,3²*2 + 1,35²*4 + 55,4²*1 + 0.54²*10 = 9647 Вт. Источники ЭДС доставляют мощность

E₁I₁ — Е₃I₃ в 120*57,3 + 50*55,4 = 9647 Вт. Так как мощность сходится, то все правильно.

17. Преобразование звезды в треугольник и треугольника в звезду. Полезность преобразования звезды в треугольник и треугольника в звезду.

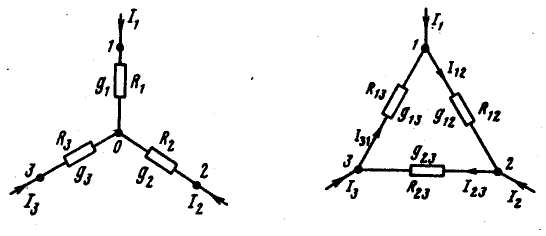Если переводить звезду в треугольник, то:

g₁₂ = g₁g₂ / ( g₁ + g₂ + g₃ );

g₂₃ = g₂g₃ / ( g₁ + g₂ + g₃ );

g₃₁ = g₃g₁ / ( g₁ + g₂ + g₃ );

Если переводить треугольник в звезду, то:

R₁ = R₁₂R₃₁ / ( R₁₂ + R₂₃ + R₃₁ );

R₂ = R₂₃R₁₂ / ( R₁₂ + R₂₃ + R₃₁ );

R₃ = R₃₁R₂₃ / ( R₁₂ + R₂₃ + R₃₁ );

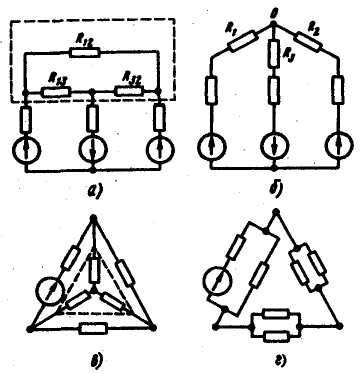
Преобразование треугольника в звезду можно пояснить,

рас­смотрев, например, схему рис. а, б. На рис. а изображена

схема до преобразования, пунктиром обведен

преобразуемый тре­угольник. На рис. б представлена та же

схема после преобра­зования. Расчет токов произвести для

нее проще (например, мето­дом двух узлов), чем для схемы

рис. а. В полезности преобразования звезды в треугольник

можно убе­диться на примере схем рис. в, г. На рис. в

изображена схема до преобразования, пунктиром обведена

преобразуемая в треугольник звезда. На рис. г представлена

схема после пре­образования, которая свелась к последовательному соединению сопротивлений.

Пример. Найти значения сопротивлений R₁, R₂, R₃ в схеме рис. б, если сопротивления R₁₂, R₁₃, R₃₂ в схеме рис. а равны соответственно 2,3,5 Ом. Решение. По формуле:

R₁ = R₁₂R₃₁ / ( R₁₂ + R₂₃ + R₃₁ ) R₁ = 2*3 / (2+3+5) = 0,6 Ом; по формуле:

R₂ = R₂₃R₁₂ / ( R₁₂ + R₂₃ + R₃₁ ); R₂ = (5*2) / 10 = 1 Ом; R₃ = (3*5) / 10=1,5 Ом.

18. Перенос источника ЭДС и источника тока.

На участке цепи рис. а между

узлами а и b имеется источник

ЭДС Е. Этот Источник можно

перенести в ветви 1 и 2, а узел а

устранить и в результате

получить участок на рис. б.

Эквивалентный пере­ход

поясняется рис. в. Точки с, d, b имеют одинаковый потенциал и потому могут быть объединены в одну точку b. Участок abc на рис. г, между крайними точками а и с которого Включен источник тока, может быть заменен участком рис. д, отличающимся от участка рис. d тем, что источник тока между точками а и с заменен на два источника, присоединен­ных параллельно R₁, и R₂. Эквивалентность замены следует из неиз­менности значений токов в каждом из узлов. Ток в узле b не изменится, так как в этот узел добавили и вычли ток J. Практически источники переносят при преобразованиях схем с целью их упроще­ния и при записи уравнений по методу контурных токов и узловых потенциалов в матрично-топологической форме записи.

19. Метод эквивалентного генератора.

По отношению к вы­деленной ветви двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника.

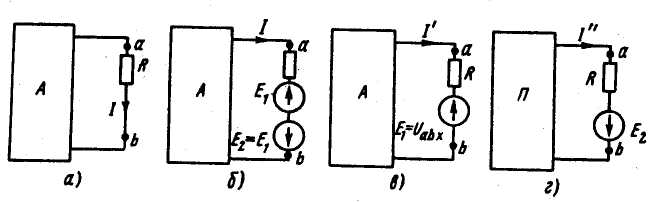Пусть задана некоторая схема и

требуется найти ток водной ее ветви.

Мысленно заключим всю схему,

содержащую ЭДС и сопротивления,

в прямоугольник, выделив из нее

ветвь ab, в которой требуется найти

ток I (рис, а). Ток I не изменится,

если в ветвь ab включить две равные и противоположно направленные ЭДС E₁ и E₂ (рис. б). На основании принципа наложения ток можно представить и виде суммы двух токов I^/ и I^// : I =I^/ + I^// .

Под током I^/ будем понимать ток, вызванный источником ЭДС E₁ и всеми источниками ЭДС и тока активного двухполюсника, включенными в прямоугольник. Ток I^// вызывается только одним источником ЭДС E₂. В соответствии с этим для нахождения токов I^/ и I^// используем схемы рис. в, г. В прямоугольнике П (рис. г) отсутствуют все источники, но оставлены их внут­ренние сопротивления. ЭДС E₁ направлена встречно напряжению U_ab. По закону Ома для участка цепи, содержащего ЭДС: I^/ = ( U_ab – E₁ ) / R. Выберем E, так, чтобы ток I^/ был равен нулю. Отсутствие тока к ветви ab эквивалентно ее размыканию (холостому ходу). Напря­жение на зажимах ab при холостом ходе ветви обозначим U_ab.

Следовательно, если выбрать E₁ = U_abx, тоI^/ = 0. Так как I = I^/ + I^//, а I^/ =0, то I = I^//. Но ток I^// в соответствии со схемой (рис. г )определяется как:

I^// = E₂ / ( R + R_вх ) = U_abx / ( R + R_вх ), где R_вх — входное сопротивление двухполюсника по отношению к зажимам ab; R — сопротивление ветви ab. Совокупность источника ЭДС Е₂ = U_abx и сопротивления R_вх можно рассматривать как некоторый эквивалентный генератор (R_вх является его внутренним сопротивлением, a U_aвх — его ЭДС). То есть:

I = I^/ + I^// = E₂ / ( R + R_вх ) = U_abx / ( R + R_вх )

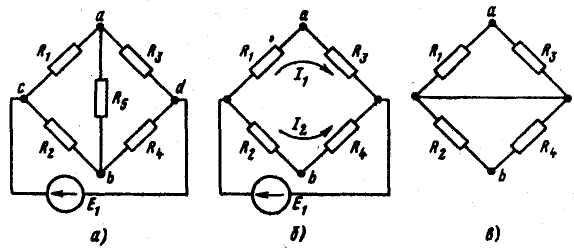
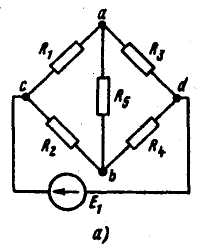
Пример. Определить ток в диагонали аb

мостовой схемы рис. а, полагая, R₁ = R₄ =

1Ом; R₂ = 4 Ом; R₃ =2 Ом; R₅ =2 Ом;

E₁ = 10 В. Решение. Размыкаем ветвь аb

(рис. б) и находим напряжение холостого

хода: ;

В.

Подсчитываем входное сопротивление всей схемы по отношению к зажимам аb

при закороченном источнике ЭДС (рис. в). Точки c и d схемы оказываются соединенными накоротко. Поэтому: Ом. Определим ток:

I = U_abx / ( R₅ + R_вх ) = 4,67 / ( 2 + 1,47 ) = 1,346 А.

20. Передача энергии от активного двухполюсника нагрузке.

Если нагрузка R подключена к активному двухполюснику, то через нее потечет ток

I = U_abx / (R + R_вх ) и в ней выделится мощность: P = I²R = U²_abxR / ( R + R_вх )² . Для того, чтобы в сопротивлении нагрузки выделялась максимальная мощность соотношение между сопротивле­нием нагрузки R и входным сопротивлением двухполюсника R_m должно быть: R = R_вх. Максимальную мощность, которая может быть выделена в нагрузке R:

P_max = U²_abx / 4R_вх. Полезную мощность, выделяющуюся в нагрузке, определяют по уравнению P = I²R = U²_abxR / ( R + R_вх )². Полная мощность, выделяемая эквивалентным генератором: P_полн = U_abxI = U²_abx / ( R + R_вх ). Коэффициент полезного действия η = P / P_полн = R / ( R + R_вх ). Если R = R_вх . Если мощность R значительна, то работать с таким низким КПД, как 0,5, недопустимо. Но если мощность Р мала и составляет всего несколько милливатт (такой мощностью обладают, напри­мер, различные датчики устройств автоматики), то с низким КПД можно не считаться, поскольку достигнута главная цель — в этом режиме датчик отдает нагрузке максимально возможную мощ­ность. Выбор сопротивления нагрузки R, равного входному сопро­тивлению R_вх активного двухполюсника, называют согласованием нагрузки.

Пример. При каком значении сопротивления R₅, а)в нем выделяется

максимальная мощность и чему она равна? Решение. Из условия R = R_вх

находим R₅ = R_вх = 1,47 Ом; P_max = U²_abx / 4R_вх = 4,67² / ( 4*1,47 ) = 3,71 Вт.