
- •Определение двойного интеграла
- •Свойства двойного интеграла
- •Приведение двойного интеграла к повторным в случае прямоугольной области
- •Приведение двойного интеграла к повторным в случае криволинейной области
- •Замена переменных в двойном интеграле
- •Вычисление двойного интеграла в полярной системе координат
- •Двойной интеграл в полярных координатах
- •Вычисление объема с помощью двойного интеграла
- •Вычисление площади поверхности с помощью двойного интеграла
- •Тройной интеграл и его свойства
- •Вычисление тройного интеграла в декартовой системе координат
- •Замена переменных в тройном интеграле
- •Вычисление тройного интеграла в цилиндрической и сферической системах координат
- •Криволинейные интегралы первого рода. Свойства
- •Вычисление криволинейных интегралов первого рода
- •Криволинейные интегралы второго рода. Свойства. Вычисление
- •Теорема Грина-Римана
- •Условие независимости криволинейного интеграла второго рода от пути интегрирования (случай плоской кривой)
- •Поверхностный интеграл первого рода. Свойства. Вычисление
- •Поверхностный интеграл второго рода. Свойства. Вычисление
- •Теорема Остроградского –Гаусса
- •Теорема Стокса (без доказательства). Условия независимости криволинейного интеграла от пути интегрирования (случай пространственной кривой)
- •Элементы теории поля
- •Множество комплексных чисел. Стереографическая проекция
- •Дифференцируемость функции комплексного переменного
- •Условия Коши-Римана
- •Интеграл от функции комплексного переменного. Свойства. Вычисление
- •Теоремы Коши для аналитической функции в односвязной области
- •Теоремы Коши для аналитической функции в многосвязной области
- •Интегральная формула Коши для аналитической функции
- •Ряд Тейлора аналитической функции
- •Изолированные особые точки аналитической функции
- •Вычет в изолированной особой точке
- •Вычисление вычетов в изолированной особой точке
- •Основная теорема о вычетах
- •Ортогональность тригонометрической системы функций
- •Ряд Фурье по тригонометрической системе функций . Теорема Дирихле
- •Тригонометрический ряд Фурье для четных и нечетных функций
- •Тригонометрический ряд Фурье в комплексной форме
- •Прямое и обратное преобразование Фурье
Интегральная формула Коши для аналитической функции
П усть
f(z)-
аналитичная в односвязной области G
и на контуре Г, ограничивающую эту
область G
и пусть точка Z
любая точка внутри контура, тогда имеет
место интегральная формула Коши:
усть
f(z)-
аналитичная в односвязной области G
и на контуре Г, ограничивающую эту
область G
и пусть точка Z
любая точка внутри контура, тогда имеет
место интегральная формула Коши:
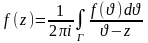
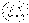
Доказательство: - окружность с центром в точке z и радиусом причем G. По теореме Коши для составного контура будем иметь.

Доказав (**). Подставим в (***).
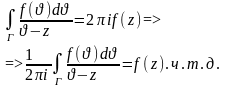
Ряд Тейлора аналитической функции
Ряд Лорана аналитической функции
(29-30)
Тейлор: Если в точке z0 f(z) аналитична, то в окрестности этой точки она представима рядом
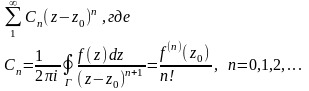
где Г- окружность с центром в точке z=z0 , целиком лежащая в окрестности точки z0 , в которой функция f(z) аналитична.
Лоран (о разложении функции в ряд по целым степеням).
Функция
f(z),
аналитическая в кольце
r
< | z
- z0
| < R,
![]() представляется
в этом кольце сходящимся рядом по целым
степеням, т.е. имеет место равенство:
представляется
в этом кольце сходящимся рядом по целым
степеням, т.е. имеет место равенство:
![]() (1)
(1)
Коэффициенты
ряда вычисляются по формуле:
![]() (2)
где
(2)
где
![]() -
произвольный контур, принадлежащий
кольцу и охватывающий точку z0;
в частности,
-
окружность
-
произвольный контур, принадлежащий
кольцу и охватывающий точку z0;
в частности,
-
окружность
![]()
Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f(z).
Совокупность
членов ряда с неотрицательными степенями
![]() называется
правильной частью ряда Лорана, члены с
отрицательными степенями образуют
главную часть ряда Лорана:
называется
правильной частью ряда Лорана, члены с
отрицательными степенями образуют
главную часть ряда Лорана:
![]() или
или
![]()
Для
коэффициентов ряда имеет место формула
оценки коэффициентов - неравенство
Коши:
![]() где
где
![]() r
- радиус контура интегрирования в
формуле (2).
r
- радиус контура интегрирования в
формуле (2).
На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f(z) - его суммы.
Частными
случаями рядов Лорана являются разложения
функции в окрестности особой точки z0
(r
= 0) и в окрестности бесконечно удаленной
точки (z0
= 0,
![]() ).
).
При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами
Изолированные особые точки аналитической функции
Точка называется и.о.т. ФКП f(z)если в некоторой окрестности точки а f(z) аналитична всюду кроме самой точки а, т.е. в окрестности точки а других точек нет.
Разложение функции f(z) в ряд Лорана сходящийся к f(z) во всех точках круга с центром в и.о.т. а, кроме самой точки а называется разложением функции f(z) в ряд Лорана в окрестности и.о.т. а.
Z0- устранимая особая точка f(z),если предел f(z) равен конечному числу.
Пусть в окрестности точки а f(z) ограничена (т.е. const=M>0, |f(z)|M в любой точке z из окрестности точки а) тогда в ряде Лорана главной части нет, есть только правильная. И этот ряд имеет сходимость во всех точках окрестности точки а, кроме самой точки а. Тогда пусть f(a)=C0, будем считать точка а правильной точкой f(z).
Z0 – устранимая особая точка f(z), если предел функции в этой точке равен const.
Если точка Z0 – устранимая особая точка, то ряд Лорана состоит только из правильной части.
Пусть f(z) неограниченна в окрестности точки а и предел в этой точке равен бесконечности, тогда точка а полюс f(z).
Если а полюс то предел равен бесконечности.
Также эта точка является нулем для функции (f(z))–1
Вывод : точка а является полюсом для f(z) порядка n ,если она является нулем для функции (f(z))–1 n‑ого порядка.
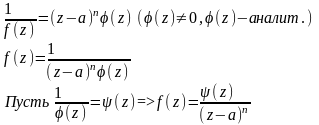
Точка а – полюс , когда f(z) можно представит в виде (см.вверх). т- порядок полюса.
Если а полюс порядка n для f(z) тогда и только тогда ,когда разложение в ряд Лорана в окрестности точки а содержит в главной части ровно n ненулевых членов.n<.
Точка а существенно особая точка функции f(z), если предел в этой точке не существует.
Точка а с.о.т. f(z), если главная часть ряда Лорана содержит бесконечное число членов отличных от 0
Рассмотри точку z= - особая точка.
Учитывая разложение в ряд Лорана при z=.
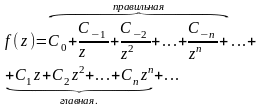
исследование идет через замену =1/z.
