Ортогональность тригонометрической системы функций
Система
функций
,
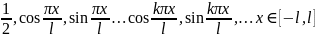(1)
называется основной тригонометрической
системой. Эта система ортогональна на
отрезке
.
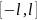Можно
показать, подсчитав интегралы вида
и
,
что система (1)
является ортогональной системой на
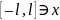и на любом отрезке оси OX,
длиной 2l:
,
.
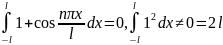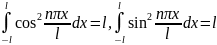От системы (1)
можно перейти к системе
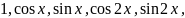
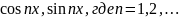путем
замены переменной:
.
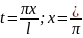Ряд Фурье по тригонометрической системе функций . Теорема Дирихле
Пусть
функция
абсолютно
интегрируема на отрезке
,
то есть существует
.
Тогда ей можно поставить в соответствие
ее тригонометрический ряд Фурье:
. Коэффициенты тригонометрического
ряда Фурье называют коэффициентами
Фурье и вычисляют по формулам Эйлера-Фурье:
.
Если функция
кусочно-гладкая
на отрезке
,
то ее тригонометрический ряд Фурье
сходится в каждой точке этого отрезка.
При этом, если
-
сумма ряда Фурье, то для любого
.
То есть, если
непрерывна
в точке
,
то
.
Если в точке
у
разрыв
первого рода, то ряд Фурье сходится к
среднеарифметическому левого и правого
пределов функции в точке
.
Дирихле:
Будем говорить, что функция f(t) удовлетворяет условиям Дирихле на отрезке [a,b], если выполняются условия:
f(t) непрерывна на [a,b] или имеет лишь конечное число точек разрыва первого рода.
f(t) монотонна на отрезке [a,b] (подразумевается строгая и нестрогая монотонность), либо функция имеет лишь конечное число экстремумов на [a,b]
Теорема Дирихле.
Пусть f T-периодическая функция и на любом отрезке [a,b] удовлетворяет условиям Дирихле, тогда:
Ряд Фурье сходится на всей числовой оси.
Сумма ряда Фурье равна f(t) во всех точках непрерывности этой функции
В точках разрыва первого рода сумма ряда Фурье равна полусумме левого и правого пределов функции f(t) в этих точках разрыва.
Пусть S(t) сумма ряда Фурье, тогда 3е условие теоремы аналитически записывают следующим образом:
ti – точка разрыва 1го рода.
Тригонометрический ряд Фурье для четных и нечетных функций
Случай
четных и нечетных функций.
-четная;
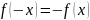- нечетная. Свойства:
1) Произведение двух четных или двух нечетных функций – есть функция четная. 2) Произведение четной на нечетную функций – есть нечетная функция.
3)
Функция
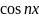является четной функцией при любом
.
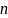Функция
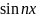является нечетной при любом
.
Ряд
Фурье для функций:
1) Если
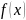четная функция, то
,
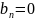таким образом ряд Фурье принимает вид:
(разложение
по косинусам) 2) Если
нечетная функция, то
,
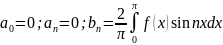следовательно, ряд Фурье:
(разложение
по синусам)
Тригонометрический ряд Фурье в комплексной форме
Как
известно из курса алгебры, экспонента
от чисто мнимого аргумента определяется
равенством
.Отсюда
немедленно вытекают формулы Эйлера
справедливые
для всех вещественных чисел
.
Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:
где использованы обозначения
Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов cn:
Итак, мы видим, что для всех значений n коэффициенты cn ищутся по одной формуле
При этом имеет место разложение
называемое комплексной формой ряда Фурье