Числовые характеристики рассеяния

Рассмотренные выше числовые характеристики служат для описания распределения с точки зрения его центральной тенденции, т. е. с точки зре­ния тенденции наблюденных значений признака группироваться вокруг некоторого их среднего значения. Наряду с этим всякое распределение харак­теризуется также рассеянием или отклонением значений наблюденного признака от его среднего значения. Существует несколько видов числовых характеристик рассеяния, среди которых наиболее распространенными явля­ются следующие: а) размах, б) половина интерквартильного размаха (полу­размах квартилей), в) среднее отклонение и г) среднее квадратическое откло­нение. Мы разъясним смысл первых трех характеристик рассеяния, но для оценки варьирования (колеблемости) наблюденных значений в рассматри­ваемом нами примере мы будем пользоваться только средним квадратическим отклонением. Самой доступной для понимания и простейшей в вычислитель­ном отношении является характеристика, называемая размахом. Размах — это разность между наибольшим и наименьшим значениями наблюденного признака. Очевидно, что размах зависит от колеблемости экстремальных значений признака. Как будет показано дальше, размах представляет собой очень важную характеристику колеблемости наблюденных значений при­знака при статистическом контроле качества и часто применяется для вычи­сления среднего квадратического отклонения.

Полуразмах квартилей составляет половину разности между первым и третьим квартилями. Первый квартиль представляет собой значение приз­нака, выше которого расположено 75% всех наблюденных значений приз­нака. Второй квартиль представляет собой значение признака, выше (и ниже) которого расположено соответственно 50% всех наблюденных значений (иначе говоря, он совпадает с медианой). Третий квартиль представляет собой значение признака, выше которого расположено 25% наблюденных значений. Полуразмах квартилей определяется по формуле

где (?з и — соответственно третий и первый квартили.

22

Среднее отклонение представляет собой среднее арифметическое абсолют­ных отклонений всех наблюденных значений признака от средней арифмети­ческой этих значений. Эта характеристика, как и полуразмах квартилей, применяется редко из-за трудностей, связанных с ее вычислением. Она опре­деляется по формуле

где— абсолютное отклонение наблюденного значения признака;

— число наблюдений. Среднее квадратическое отклонение представляет собой корень квадрат­ный из среднего квадрата отклонений от средней арифметической всех наблю­денных значений признака. Эта характеристика при определенных условиях называется также стандартной ошибкой.

Формулой, из которой выводятся все прочие вычислительные формулы, здесь служит следующая *:

Эта характеристика является одной из наиболее употребительных и стабиль­ных характеристик рассеяния. Раскрытие большинства индуктивных аспек­тов статистического метода находится в прямой зависимости от вычисленной или предположительной оценки среднего квадратического отклонения. «Поль­зуясь языком механики, можно сказать, что если п значений х определяют положение п одинаковых по весу частиц, то среднее квадратическое откло­нение соответствует радиусу инерции, измеряющему положение этих частиц по отношению к центру тяжести... Оно выражается в тех же единицах изме­рения, что и наблюденные признаки; если последние измеряются, скажем, в фунтах, то и среднее квадратическое отклонение измеряется также в фун­тах» ².

Формула определения среднего квадратического отклонения на основе неупоря­доченных данных

Формула определения среднего квадратического отклонения на основе распре­деления частот

Применяя последнюю формулу, получим для нашего примера

¹ В справочнике по контролю качества промышленных материалов (ASTM Manual on Quality Control of Materials) по поводу формулы среднего квадратического отклонения сказано следующее: «В некоторых работах по статистике термин среднее квадратическое отклонение выборки применяется для обозначения квадратного корня из отношения суммы квадратов отклонений от среднего значения выборки к п — 1, где п обозначает объем выборки. По сути, это выражение представляет собой корень квадратный из несме­щенной оценки универсальной дисперсии (а²), основанной на выборке, а не из несме­щенной оценки универсального среднего квадратического отклонения. Кроме того, если несмещенную оценку требуется определить в каждой точке, i/c₂o то ее, можно найти... графически, но это делается очень редко, так как связано со сложными вычислениями». Поэтому, если требуется получить несмещенную оценку среднего квадратического откло­нения, то для определения последней проще всего воспользоваться таблицей коэффи­циентов с₂ (см. табл. А. Приложение I).² ASTM Committee Е-11, ASTM Manual on Quality Control of Materials, Philadel­phia: American Society for Testing Materials, 1951, p. 15.

ДРУГИЕ СТАТИСТИЧЕСКИЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

Отношение среднего квадратического отклонения к средней арифмети­ческой дает новую числовую характеристику вариации признака, иногда весьма полезную и применяемую в производстве наряду с другими статисти­ческими характеристиками. Это отношение носит название коэффициента вариации и определяется по формуле

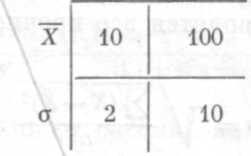
Чтобы проиллюстрировать применение этого коэффициента, предположим, что имеются две статистические совокупности, характеризуемые 1ио.

Выбо рки

Среднее квадратическое отклонение выборки 1 меньше, чем среднее квадра-тическое отклонение выборки 2, но коэффициент вариации признака в выбор­ке 2 намного меньше, чем в выборке 1.

\ 12

Существуют и другие числовые характеристики распределения, пред­ставляющие известный интерес — как практический, так и теоретический. Коэффициент скошенности, или асимметрии, характеризует тенденцию к рассеянию в одном направлении больше, чем в другом. Коэффициент отно­сительной скошенности определяется по формуле

Разумеется, для симметричного распределения зк = 0. Если значение коэффициента жА; отрицательное, то большая часть ряда распределения рас­полагается слева от оси ординат (У); если положительное, то справа от нее.

Эксцесс характеризует островершинность распределения. Относитель­ный эксцесс определяется по формуле

Для теоретического нормального распределения, которое рассматривается в следующем параграфе, коэффициенты вк и К равны нулю.