8 Контрольные точки

Произвольно выбираем несколько значений и находим значения функции - Контрольные точки (x, помогают более точно построить график функции.

9 Построение графика функции

Построим графики функций , используя результаты исследования в п.1-7

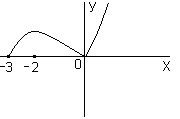
Рис.6

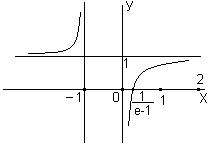
Рис.7

Замечание После того как рассмотрите построение графиков сопоставьте с результатами исследования.

10 Образцы выполнения исследования функции и построения графиков

Исследовать поведение функции и построить график.

10.1

1 Область определения

Данная функция, существует при любом действительном значении х, тогда .

2 Исследование функции на четность и нечетность

Так как область определения функции множество четное относительно начала координат, то найдем :

.

Видим, что и , значит функция ни четная ни нечетная, т.е. функция общего вида.

3 Точки пересечения графика функции с осями координат

С осью : полагаем и, подставляя это значение в данную функцию , находим . Получим точку .

С осью : полагаем , находим из уравнения (*)

Корни уравнения являются делителями свободного члена 16. Следовательно, попробуем подставить в уравнение (*) числа:

При : получаем , следовательно является корнем уравнения (*). Тогда многочлен делится на без остатка. Выполним деление:

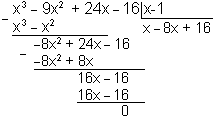
Итак, . Уравнение (*) принимает вид: , откуда (эти значения называют нулями функции). Таким образом, график функции пересекает ось в точках: .

4 Промежутки знакопостоянства функции. Исследование функции на концах промежутков знакопостоянства

Промежутки знакопостоянства функции разделяют точки разрыва и нули функции. Для данной функции – это . Обратите внимание, что кратный корень, значит в интервалах прилегающих к этой точке функция знак не меняет. Изобразим их на числовой оси:

Знак функции определяется непосредственной подстановкой любого значения из полученных интервалов в аналитическое выражение функции.

Если на интервале функция отрицательная, то ее график располагается под осью , на интервалах функция положительная, то над осью .

Для выяснения поведения функции на концах промежутков знакопостоянства

Найдем пределы функции при :

;

, таким образом, знак бесконечности определяется знаком старшего члена . Это означает, что слева график функции уходит неограниченно вниз, а справа – неограниченно вверх.

5 Асимптоты графика функции

Т.к. функция не имеет бесконечных разрывов, то вертикальные асимптоты отсутствуют.

Для отыскания наклонных асимптот , найдем :

, т.к , то график функции наклонных асимптот не имеет.

6 Исследование функции на монотонность. Точки экстремума

Найдем критические точки функции. Согласно необходимого условия экстремума: в точках экстремума производная равна нулю или не существует.

Найдем производную: .

Решим уравнение :

;

;

Производная функции обращается в нуль в точках и - критические точки. Они делят область определения на интервалы монотонности (интервалы убывания и возрастания).

Интервалы изобразим их на числовой оси (рис.8):

Рис.8

Поведение функции на каждом интервале определяется знаком производной.

Для определения знака производной на каждом интервале достаточно взять любое значение из этого интервала и подставить в производную .

На интервале , возьмем любое , например , и подставим в производную . Получили , следовательно функция на интервале возрастает.

Аналогично устанавливаем:

– на интервале , следовательно функция убывает;

– на интервале , следовательно функция возрастает.

Знаки производной проставлены на рисунке 8 в каждом интервале. Стрелками схематично указано поведение функции .

Замечаем, что при переходе через точку производная меняет знак, с «+» на «-». Это означает, что в точке функция имеет максимум (на основании достаточного условия существования экстремума). Найдем значение при : .

Значит, точка максимума .

При переходе через точку производная меняет знак с «-» на «+». Это означает, что при функция имеет минимум: . Точка минимума .

7 Исследование графика функции на выпуклость и вогнутость. Точки перегиба

Это исследование проводится с помощью второй производной. Найдем точки, подозрительные на перегиб, используя необходимое условие перегиба: в точках перегиба вторая производная либо равна нулю, либо не существует.

Так как , то и существует при любых . Приравняем вторую производную к нулю и найдем корни уравнения: .

Отсюда – точка, подозрительная на перегиб. Точка делит область определения на интервалы и

Рис.9

Определим знак второй производной на каждом из полученных интервалов, непосредственным способом.

На интервале получаем , значит, при график функции вогнутый (), рисунок 8.

На интервале получаем , значит, при график функции выпуклый (), рисунок 8.

Так как при переходе через точку вторая производная меняет знак, то график меняет выпуклость на вогнутость, то есть абсцисса точки перегиба.

.

Точка перегиба .

8 Контрольные точки

Для более точного построения графика найдем насколько дополнительных точек: , точка

9 Построение графика по полученным результатам исследования

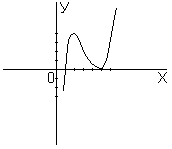
Замечание При исследовании будем использовать только краткую запись, так как все действия аналогичны исследованной функции .

10.2

1 Область определения

2 Исследование функции на четность и нечетность

Так как область определения множество симметричное относительно начала отсчета, то найдем :

.

Делаем вывод: функция нечетная. Для дальнейшего исследования будем использовать свойства нечетной функции на симметричных интервалах:

– меняет знакопостоянство;

– сохраняет монотонность;

– точки максимума и минимума симметричны относительно начала координат;

– меняет выпуклость на вогнутость;

– график функции симметричен относительно начала координат.

3 Точки пересечения графика функции с осями координат

С осью : .

Решим уравнение:

.

Получили точки:

С осью : .

. Получили точку .

4 Промежутки знакопостоянства функции. Исследование функции на концах промежутков знакопостоянства

Для выяснения поведения функции на концах промежутков знакопостоянства вычислим следующие пределы:

5 Асимптоты графика функции

5.1 Так как в точках функция претерпевает бесконечный разрыв, то график функции имеет вертикальные асимптоты :

5.2

.

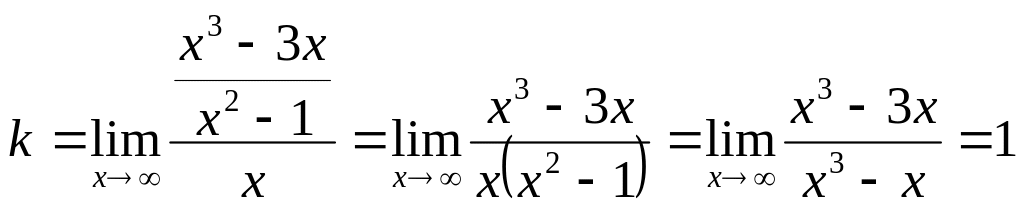
Получили – наклонная асимптота.

6 Исследование функции на монотонность. Экстремумы функции

Решим уравнение :

Критические точки (по первой производной): точек, в которых производная равна нулю нет,

Отметим на числовой прямой критические точки и исследуем знак производной на каждом из полученных интервалов

Делаем вывод, что функция возрастает на всей области определения.

Так как функция в области определения монотонности не меняет, то точек экстремума нет.

7 Исследование графика функции на выпуклость и вогнутость. Точки перегиба

Найдем вторую производную функции:

.

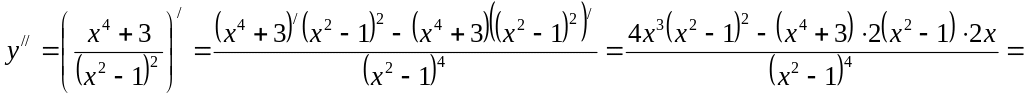
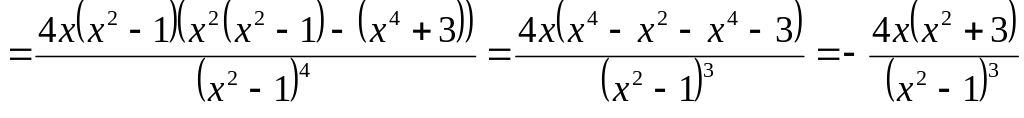Решим уравнение :

Критические точки (по второй производной):

Отметим на числовой прямой полученные точки и исследуем знак второй производной

При график функции имеет перегиб.

Точка – точка перегиба.

9 Контрольные точки

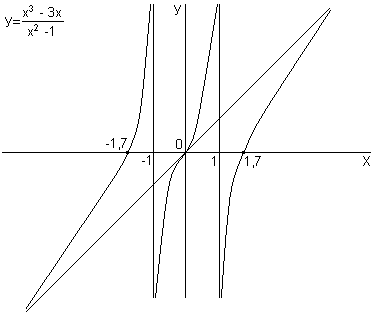
9 Построение графика по полученным результатам исследования

При построении графика помним, что он симметричен относительно точки .

11.3

Замечаем, что функция задана в неявном виде. Выразим y в явном виде

.

Достаточно исследовать и построить график функции , а за тем отобразить симметрично оси OX.

1 Область определения функции

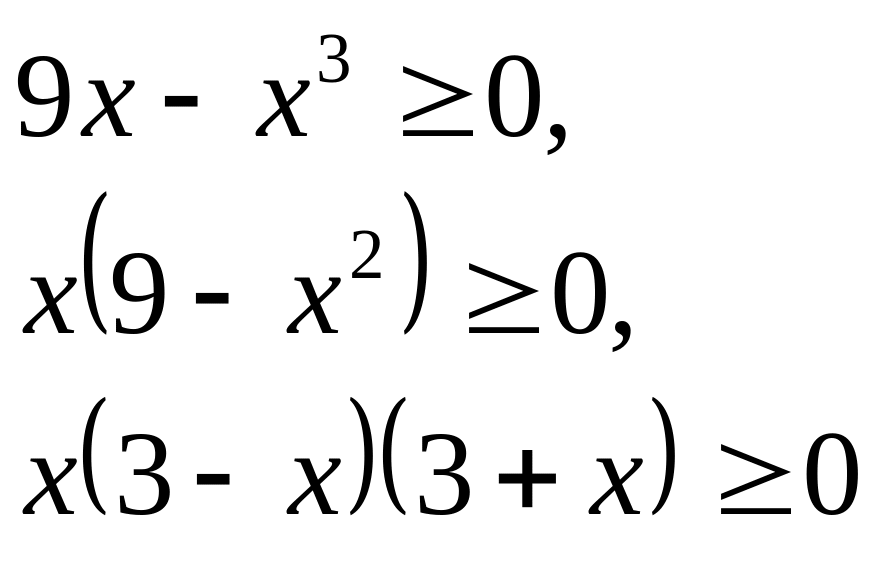
Решим методом интервалов: .

Делаем вывод: . На интервалах и функция в дальнейшем не исследуется, т.к. они не входят в область определения.

2 Исследование функции на четность и нечетность

Так как область определения множество несимметричное относительно начала координат, то делаем вывод, что функция ни четная ни нечетная.