1.3 Характеристики и устойчивость сар

Статичные и динамические характеристики

Свойства САР и динамических звеньев определяются их статическими и динамическими характеристиками. Эти характеристики можно получить экспериментальным или расчётным образом.

Статичной характеристикой звена или системы называется зависимость выходной величины от входной в установившемся режиме.

Динамической характеристикой звена или системы называется зависимость выходной величины от входной за время переходного процесса.

Примером статичных характеристик могут быть характеристики, которые приведены на рисунке 1.15.

Динамические характеристики подразделяют на временные (переходные) и частотные.

Временными характеристиками динамических звеньев или САР называют зависимость протекания переходных процессов во времени при подаче на их вход воздействия определенного вида. Наиболее важной временной характеристикой является та, которая имеет место при одинаковом мгновенном скачкообразным изменении входной величины. Такой сигнал показан на рисунке 1.20а. Как видно из рисунка 1.20б, сигнал произвольной формы может быть предоставлен через скачкообразные сигналы.

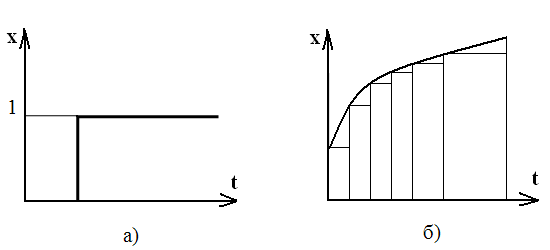
Рисунок 1.20 - Входные сигналы: а) одинаковый скачкообразно мгновенно изменяемый; б) произвольной формы с представлением его через сигнал типа (а).

Примером временных динамических звеньев могут быть характеристики, которые приведенные на рисунках 1.4, 1.6, 1.8 и 1.10.

К частотным динамическим характеристикам относят амплитудно-фазовую, амплитудно-частотные и фазачастотные характеристики. Когда на вход звена или системы подается сигнал

x=А_хsint (1.24)

с амплитудой А_х, то после затухания переходных процессов на выхождении звена или системы будет иметь место сигнал с амплитудой А_y и сдвигом фаз .

y=А_ysin(t+) (1.25)

Если выражения для y и x перевести на комплексные плоскости и найти их отношение, то можно получить выражение амплитудно-фазовой характеристики W(j).

(1.26)

где U() и V() - реальная и мнимая части амплитудно-фазовой характеристики.

Амплитудно-фазовая характеристика может быть также получена сменой в передаточной функции оператора p на j.

Амплитудно-фазовой характеристикой (АФХ) системы называется отношение выходной величины к входной, выраженное в комплексной форме.

Рисунок 1.21 - Пример амплитудно-фазовой характеристики

Амплитудно-частотной характеристикой называется зависимость отношений амплитуд выходного и входного сигнала от частоты.

Фазочастотной характеристикой называется зависимость разности фаз выходного и входного сигнала от частоты

В последних двух характеристиках частоту  откладывают, как обычно, по логарифмической шкале. Поэтому эти характеричтики часто называют логарифмическими.

Рисунок 1.22 - Пример логарифмических характеристик

Задача 2. Построить амплитудно-фазовую характеристику для динамического звена, которая имеет передаточную функцию W(p)=2p²-5p+1.

Решение. Для получения выражения амплитудно-фазовой характеристики заменяем в передаточной функции p на j. С учётом того, что j²=—1 получим

W(j)=2(j)²-5j+1=-2²-j5+1=(-2²+1)-j5

Записываем отдельно реальную U() и мнимую V() части амплитудно-фазовой характеристики W(j) = U().

U()=-2²+1

V()=-5

Подставляем в получившиеся выражения U() и V()значения  от 0 до .

U(0)=-2*0²+1=1

U(0,1)=-2*0,1²+1=0,08

V(0)=-5*0=0

V(0,1)=-5*0,1=-0,5

и т.д.

Итоги расчётов заносим в таблицу 1. По итогам таблицы строим амплитудно-фазовую характеристику.

Таблица 1

	0	0,1	0,5	0,7	1	2	10	
U()	1	0,08	-0,5	0,02	-1	-7	-199	-
V()	0	-0,5	-2,5	-3,5	-5	-35	-50	-

Рисунок 1.23

Устойчивость САР и ее определение

Устойчивость - это свойство системы возвращаться в установившееся состояние после того, как она была выведена из этого состояния каким-либо возмущении.

Рисунок 1.24 - Примеры систем: а) устойчивой, б) неустойчивой, в) нейтрально-устойчивой

Поведение САР при изменении возмущения или управляющего воздействия могут быть описаны выражением

y=y₀+y(t) (1.27)

где y₀ - вынужденная составляющая выходной величины;

y(t) - переходная составляющая выходной величины, которая изменяется во времени.

Ради того, чтобы САР была устойчивой, необходимо чтобы с течением времени переходная составляющая выходной величины y(t) стремилась к нолю. Аналитическое выражение для y(t) может быть получено через дифференциальное уравнение, которое описывает свойства системы [смотри левую часть формулы (1.1)]. Характеристическое уравнение для (1.1) имеет вид

a_npⁿ+a_n-1p^n-1+...+a₁p+ a₀=0 . (1.28)

Характеристическое уравнение может быть также получено приравниваем нолю знаменателя передаточной функции.

Если определить все корни характеристического уравнения, то общее решение дифференциального уравнения, а значит и y(t) будут равны

y(t)=C₁e^p1t+C₂e^p2t+...+C_n-1e^pn-1t+e^pit(A₁+A₂t+A₃t²+...+A_it^i-1) (1.29)

где C₁ ,C₂,...,C_n-1 i A₁,A₂,...,A_i - постоянные интегрирования.

Из (1.29) видно, что САР будет устойчивой, если все реальные корни и реальные части комплексных корней характеристического уравнения будут отрицательные. При этом все составляющие (1.29) при увеличении времени будут приближаться к нолю.

Определить устойчивость САР через корни характеристического уравнения очень сложно, ведь это связано с решением дифференциального уравнения высокого порядка. Кроме того, такой способ определения устойчивости не позволяет получить рекомендаций по ее увеличению. Поэтому на практике, как обычно, используют косвенные методы вычисления устойчивости. При этом она определяется на основании определенных критериев, под которыми имеют в виду правила, посредством которых определяют, устойчива ли система.

Задача 3. Записать характеристическое уравнение для САР, которая имеет передаточную функцию.

Решение. Характеристическое уравнение получается приравниваем к нолю знаменателя передаточной функции. Поэтому оно равно

p³-3p²+6p+12=0 .

Критерий устойчивости Рауса-Гурвица

Для пользования критериями Рауса-Гурвица рассматривается характеристическое уравнение [смотри (1.28)], на основании которого составляется специальная таблица.

Таблица 2

№ строки	Значение r	Номер столбца
		1	2	3	…
1	—	an	an-2	an-4	…
2	—	an-1	an-3	an-5	…
3	r0= an/ an-1	c1,3= an-2 — r0·an-3	c2,3= an-4 — r0·an-5	c3,3= an-6 — r0·an-7	…
4	r1= an/ c1,3	c1,4= an-3 — r1·c2,3	c2,4= an-5 — r1·c3,3	c3,4= an-7 — r1·c4,3	…
	…	…	…	…	…
n+1	rn-2=c1,n-1/c1,n an-1	c1,n+1=c2,n-1—rn-2·c2,n=a0	0	0	0

Таблица складывается следующим образом. В первую строчку в столбцы последовательно вписывают через один коэффициенты характеристического уравнения, начиная с коэффициента при составляющей, которая имеет большую степень. Во вторую строчку по столбцам последовательно записывают остальные коэффициенты. Индексы при величинах c_k,i означают соответственно номер столбца и строчки. Значение величин r_i и c_k,i определяются последовательно во время заполнения строчек сверху вниз и слева направо.

Таким образом, для того, чтобы система была устойчивой, необходимо и достаточно, чтобы все величины первого столбца таблицы были положительными при положительном коэффициенте a₀ характеристического уравнения.

Задача 4. Определить посредством критерия Рауса-Гурвица устойчивость системы, которая имеет передаточную функцию

Решение. Записываем для заданной системы характеристичное уравнение

3p⁵+5p⁴+10p³+p²+2p+4=0

По правилам, которые приведены выше, составляем таблицу, где a₅=3, a₄=5, a₃=10, a₂=1, a₁=2, a₀=4. Коэффициенты таблицы рассчитываются по формулам

Все остальные элементы таблицы будут равны нолю. Таким образом получим таблицу (смотри таблицу 3).

Из характеристического уравнения системы видно, что коэффициент a₀ положительный. Однако, из получившейся таблицы видно, что не все элементы первого столбца положительные. Отрицательным является c_1,5= - 31,48. Таким образом исследуемая система является неустойчивой.

Таблица 3

№ строки	Значение r	Номер столбца
		1	2	3
1	—	3	10	2
2	—	5	1	4
3	0,6	9,4	—0,4	0
4	0,53	1,21	4	0
5	7,77	—31,48	0	0
6	—0,04	4	0	0

Критерий устойчивости Михайлова

Если в характеристическом уравнении (1.28) поменять p на j, то получим функцию переменного A(j). В ней можно выделить реальную и мнимую части.

A(j)=U_A()+jV_A() (1.30)

Если задаваться  от 0 до + и откладывать на комплексной плоскости вектор с центром в начале координат и концом в пунктах U() и V(), то получим характеристику, которую принято называть годографом Михайлова.

Линейная система n-га порядка будет устойчивая, если при изменении от  от 0 до  годограф Михайлова последовательно обходит n квадрантов в комплексной плоскости навстречу часовой стрелки, начиная с пункта на реальной положительной полуоси и нигде не проходит через начало координат.

Рисунок 1.25 - Примеры годографов Михайлова: а - устойчивых систем, б - неустойчивых систем.

Задача 5. Определить посредством критерия Михайлова устойчивость системы, которая имеет передаточную функцию

Решение. Записываем для заданной системы характеристическое уравнение

3p²+2p+2=0

Для получения годографа Михайлова меняем в передаточной функции p на j. Получим

A(j)=3(j)²+2j+2=-3²+2+j2.

Записываем отдельно реальную U_A() и мнимую V_A() части выражения A(j).

U_A()=-3²+2

V_A()=2.

Подставляем значения  от 0 до .

U_A(0)=-3*0²+2=2

V_A(0)=2*0=0

U_A(0,5)=-3*0,5²+2=1,25

V_A(0,5)=2*0,5=1

U_A(0,75)=-3*0,75²+2=0,31

V_A(0,75)=2*0,75=1,5

U_A(1)=-3*1²+2=-1

V_A(1)=2*1=2

U_A(2)=-3*2²+2=-10

V_A(2)=2*2=4.

Итоги расчётов занесём в таблицу 4.

Таблица 4

	0	0,5	0,75	1	2	
UA()	2	1.75	0.31	-1	-10	-
VA()	0	1	1,5	2	4	+

По полученным значениям строим годограф Михайлова (смотри рисунок 1.26). Из годографа видно, что он (для рассматриваемой системы - системы второго порядка) начинается на положительной полуоси и последовательно навстречу часовой стрелки обходит два квандранты. Значит система устойчивая.

Рисунок 1.26

Критерий устойчивости Найквиста

Критерий устойчивости Найквиста позволяет полагать об устойчивости замкнутой системы по амплитудной фазовой характеристике разомкнутой системы. Причем разомкнутая система должна быть устойчивой.

Рисунок 1.27 - Амплитудно-фазовая характеристика разомкнутых систем, в которых замкнутые системы: 1 - неустойчивая, 2 - работает на границе устойчивости, 3 - устойчивая.

Проще критерий Найквиста может быть сформулирован следующим образом: если разомкнутая система устойчива, то для обеспечения её устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не охватывала пункт (-1, j0). В обратном случае система будет неустойчивой.

Задача 6. Определить посредством критерия Найквиста устойчивость системы, которая приведена на рисунке 1.28.

Рисунок 1.28

Решение. Для получения передаточной функции разомкнутой системы в схеме, которая приведена на рисунке 1.28 убираем внешнюю обратную связь. Поскольку суммирующее приспособление не имеет своей передаточной функции, то оно также приемлемо. Таким образом, разомкнутая схема для замкнутой схемы, которая приведена на рисунке 1.28 имеет вид, приведенный на рисунке 1.29.

Рисунок 1.29

Из рисунка 1.29 видно, что передаточная функция разомкнутой системы W(p) равна W₁(p).

Переходим от передаточной функции разомкнутой системы к выражению ее амплитудно-фазовой характеристики. Ради этого меняем в W(p) p на j.

Для того чтобы выделить отдельно реальную и мнимую части выражения амплитудно-фазовой характеристики, необходимо избавиться от комплексного числа в знаменателе W(j). Это можно достичь, домножив на сопряжённый ему комплекс числитель и знаменатель.

Таким образом реальная U() и мнимая V() части функции W(j) будут равны

Подставляем значения  от 0 до , получим

и т.д. Итоги расчетов занесём в таблицу 5.

Таблица 5

	0	1	1,5	1,6	1,8	2	3	
U()	-0,08	-0,2	-0,8	-0,78	-0,37	-0,15	-0,01	0
V()	-	-0,6	-0,27	0,06	0,31	0,23	0,05	0

По итогам таблицы 5 строим амплитудно-фазовую характеристику (рисунок 1.30).

Из рисунка 1.20 видно, что амплитудно-фазовая характеристика разомкнутой системы не захватывает пункт (-1,j0). Из этого следует, что замкнутая система устойчивая.

Рисунок 1.30

Запас устойчивости САР

Выделяют запас устойчивости по модулю и по фазе. Расстояние пункта пересечения амплитудно-фазовой характеристики разомкнутой системы с отрицательной реальной полуосью до пункта (-1,j0) называют запасам устойчивости по модулю ∆L. Угол, который образовывается отрицательной реальной полуосью и прямой, которая проводится из начала координат и пункт пересечения АФХ с окружностью одинакового радиуса, принято называть запасом устойчивости по фазе ∆.

Запасы устойчивости системы по модулю ∆L и по фазе ∆ показывают, на сколько должны они измениться, чтобы система вышла на границу устойчивости.

Рисунок 1.31 – Определение запаса устойчивости по модулю и по фазе

Определение устойчивости и запаса устойчивости САР по модулю и по фазе по логарифмическим частотным характеристикам (ЛАЧХ)

Такой способ определения устойчивости основывается на критерии Найквиста. При этом пункт, где модуль амплитудно-фазовой характеристики равен 1, соответствует пункту пересечения ЛАЧХ с горизонталью L=0 дБ, а пункту в котором фазовый сдвиг равен 180, соответствует пересечению ЛАЧХ линии -.

Рисунок 1.32 - Определение устойчивости и запаса устойчивости по модулю и по фазе по логарифмическим частотным характеристикам: а) - система устойчивая, б) - система неустойчивая.

Замкнутая система устойчивая, если на частоте , для которой  = - ордината амплитудно-частотной характеристики отрицательная.